- 62-

Белгородская государственная

ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ

СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ

В.В.МУРОМЦЕВ

АЛГОРИТМЫ НА ГРАФАХ

УЧЕБНОЕ ПОСОБИЕ

БЕЛГОРОД - 2000

УДК 519.17

Муромцев В.В. Алгоритмы на графах: Учебное пособие.

Белгород: Изд. БИИММАП, 2000.- 64 с.

Даны основные понятия теории графов. Рассмотрены вопросы представления графов в памяти ЭВМ и ряд существующих алгоритмов на графах. Изложение иллюстрируется примерами сведения прикладных задач к графовым задачам. Затрагиваются общие вопросы построения эффективных алгоритмов. Приведено большое число упражнений, в которых требуется рассматривать вопросы программной реализации графовых алгоритмов и их модификации для решения прикладных задач.

Учебное пособие предназначено для студентов технических и экономических вузов, изучающих программирование.

Табл. 13. Ил. 37. Список лит.: 16 назв.

Рецензенты: Константинов И.С., д.т.н.

Жиляков Е.Г., д.т.н.

ВВЕДЕНИЕ 4

1. ОПРЕДЕЛЕНИЕ ГРАФА 7

2. ПРЕДСТАВЛЕНИЕ ГРАФОВ В ПАМЯТИ ЭВМ 10

3. НЕКОТОРЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

ТЕОРИИ ГРАФОВ 14

4. ОПЕРАЦИИ НАД ГРАФАМИ 17

5. СВЯЗНОСТЬ 20

5.1. Построение покрывающих деревьев 20

5.2. Поиск на графах 27

5.3. Сильная связность 31

5.4. Транзитивное замыкание орграфа 34

6. РАССТОЯНИЕ 35

6.1. Поиск кратчайших путей между отдельными

вершинами графа 36

6.2. Поиск кратчайших путей между каждой парой

вершин графа 43

7. ПОТОКИ 44

7.1. Условия существования потока 44

7.2. Поиск увеличивающей цепи ..46

7.3. Поиск максимального потока 48

7.4. Поиск потока минимальной стоимости 49

7.5. Задача почтальона для орграфа 53

СПИСОК ЛИТЕРАТУРЫ 60

Введение

Теория графов представляет собой раздел математики, имеющий широкое практическое применение. В её терминах формулируется большое число задач, связанных с дискретными объектами. Такие задачи возникают при проектировании интегральных схем и схем управления, электрических цепей, блок-схем программ, в экономике, статистике, химии, биологии и в других областях. Теория графов становится одной из существенных частей математического аппарата кибернетики, языком дискретной математики.

В отличие от других научных дисциплин, теория графов имеет вполне определенную дату рождения. Первая работа по теории графов, написанная швейцарским математиком Леонардом Эйлером (1707-1783), была опубликована в 1736 году в Трудах Академии наук в Санкт-Петербурге. Исследование Эйлера было проведено в связи с популярной в то время задачей о кенигсбергских мостах. Эта задача имеет следующую формулировку:

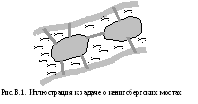
Задача 1.Город Кенигсберг, располагавшийся в восточной Пруссии, был построен в месте слияния двух рек на их берегах и на двух островах. В городе было семь мостов, которые соединяли острова между собой и с береговыми частями города (рис.В.1). Необходимо ответить на вопрос: мог ли любой житель Кенигсберга, выйдя из дома, пройти по всем семи мостам города в точности по одному разу и вернуться домой?

Ответ на вопрос, поставленный в данной задаче, должен быть отрицательным. Эйлер дал этот ответ и нашел критерий существования маршрута, удовлетворяющего требованиям задачи.

Однако результат, полученный Эйлером, более ста лет оставался единственным результатом теории графов.

Развитие теории графов в конце XIXи началеXXвв. было связано с распространением представлений о молекулярном строении вещества и становлением теории электрических цепей. К 50-м годам нашего века в теории графов сложились два различных направления: алгебраическое и оптимизационное.

Например, поиск ответа на поставленный в задаче 1 вопрос относится к алгебраическому направлению теории графов. Изменим задачу 1.

Задача 2.Отличие задачи 2 от задачи 1 состоит в том, что требуется найти маршрут, по которому житель, выйдя из дома, пройдет по каждому мосту хотя бы один раз и вернется домой, причем длина маршрута должна быть минимальной.

Задача поиска такого маршрута относится к оптимизационному направлению теории графов. Вопросам решения задачи 1 и задачи 2 будет уделено место в гл.7.

Оптимизационное направление получило широкое развитие благодаря появлению ЭВМ, так как для эффективного использования ЭВМ при решении прикладных задач с использованием теории графов необходимы эффективные алгоритмы решения графовых задач.

Под эффективным алгоритмом понимают такой алгоритм, сложность которого (число шагов или время работы) выражается полиномиальной функцией от размерности (некоторого параметра, характеризующего длину записи условий задачи).

Для тех, кто считает, что неэффективность алгоритма может быть компенсирована увеличением быстродействия ЭВМ, приведены таблицы В.1 и В.2 [1].

Как следует из таблицы В.1, например, при сложности 3ⁿдаже увеличение быстродействия ЭВМ в 1000 раз по сравнению с имеющимися в настоящее время позволяет увеличить размерность задачи, которая доступна для расчета лишь на 6 или 7 единиц. А из таблицы В.2 видно, что при той же сложности задача размерности 33 единицы будет решаться около трех веков. Вот почему необходимо искать пути уменьшения сложности. То есть применять эффективные алгоритмы для решения задачи. Однако эффективные алгоритмы существуют не для всех задач. Причем среди задач, для которых пока нет эффективных алгоритмов, есть задачи, составляющие особый класс. Если будет найден эффективный алгоритм для решения хотя бы одной задачи из этого класса, то это будет означать, что эффективный алгоритм найден для всех задач этого класса.

Задачи, для которых не найден эффективный алгоритм решения, можно решать, используя эвристические или приближенные алгоритмы, которые дают результат за приемлемое время, но этот результат не является точным, а имеет какую-то погрешность.

Эвристическиминазывают алгоритмы, основанные на неформальных соображениях. Корректность таких алгоритмов теоретически не обоснована.

Рассмотрению некоторых существующих в настоящее время эффективных графовых алгоритмов посвящено данное пособие.

Таблица В.1. Влияние технического совершенствования ЭВМ на полиномиальные и экспоненциальные алгоритмы

Слож-ность	Размеры наибольшей задачи, разрешимой за 1 час.
	На современных ЭВМ	На ЭВМ в 100 раз более быстрых	На ЭВМ в 1000 раз более быстрых
N	N1	100 N1	1000 N1
n^2	N2	10 N2	31.6 N2
n^3	N3	4.64 N3	10 N3
n^5	N4	2.5 N4	3.98 N4
2^n	N5	6.64+N5	9.97+N5
3^n	N6	4.19+N6	6.29+N6

Таблица В.2. Максимальная размерность задач, разрешимых за данное время

Сложность	Время решения задачи
	1 с.	10 ^2с. 1.7 мин.	10 ^4с. 2.7 ч.	10^6с. 12 сут.	10^8с. 3 года.	10 ^10с. 3 века.
1000n	10^3	10^5	10^7	10^9	10^11	10^13
1000nlog n	140	7.710^3	5.210^5	3.910^7	3.110^9	2.610^11
100n^2	10^2	10^3	10^4	10^5	10^6	10^7
10n^3	46	2.110^2	10^3	4.610^3	2.110^4	10^5
2^n^/3	59	79	99	119	139	159
2^n	19	26	33	39	46	53
3^n	12	16	20	25	29	33