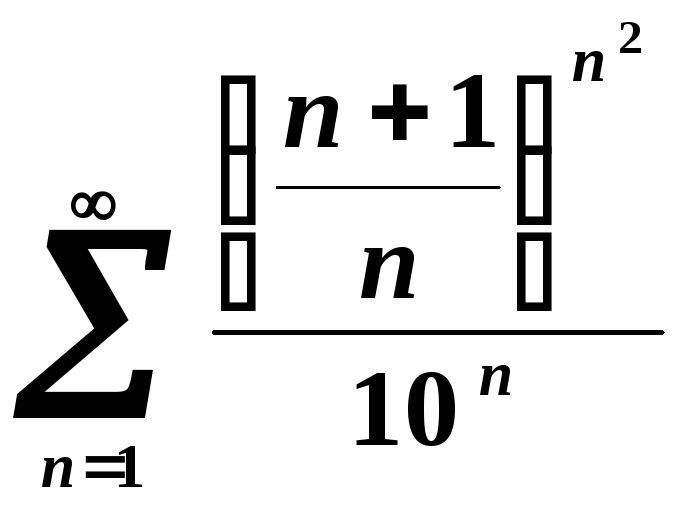матан 3 курс 2013 / лекции / Числові ряди / лекция № 20
.docМІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ
ЛЕКЦІЯ № 20
з теми: «Ознаки збіжності рядів з невід’ємними членами.»
Модуль КЗН-02.ПР.О.03.10 Числові ряди
Дисципліна: «Математичний аналіз»
|
Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики.
Протокол № ____ від _______20__ р.
Голова циклової комісії ПМ Велікодна О. В.
|
Розробив викладач Велікодна О. В.
|
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІІ
Викладач: Велікодна Ольга Володимирівна.
Тема: Ознаки збіжності рядів з невід’ємними членами.
Мета:
-
Дидактична: розглянути поняття числового ряду, різновиди числових рядів. Вивчити поняття збіжності ряду та достатні умови збіжності рядів з невід’ємними членами.
-
Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.
-
Методична: вдосконалювати методику проведення лекції з використанням методики проектної технології.
Тип: лекція
Вид: лекція з використанням проектної технології.
Методи та форми проведення заняття: мовні, пояснювально-ілюстративні, проблемно-пошукові, наочні.
Науково-методичне забезпечення:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.
Між предметні зв’язки:
-
Дисципліни, що забезпечують: елементарна математика
-
Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.
Обладнання: зошити, ручки, крейда, дошка.
ХІД ЗАНЯТТЯ
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Актуалізація опорних знань: визначення числового ряду, часткових сум числового ряду, суми числового ряду, визначення збіжного та розбіжного числових рядів, необхідна умова збіжності числового ряду, властивості збіжного числового ряду, критерій Коші збіжності числового ряду, приклади збіжних та розбіжних числових рядів.
-
Вивчення нового матеріалу:
-
Тема лекції: Ознаки збіжності рядів з невід’ємними членами.
-
Мотивація вивчення матеріалу: вивчити основні методи дослідження числових рядів для подальшого їх застосування як при розв’язанні математичних, так і прикладних задач.
-
План вивчення нового матеріалу: надається в конспекті лекції.
-
Виклад нового матеріалу. Конспект лекції надається.
-
Закріплення нового матеріалу.
-
Підсумки заняття.
-
Домашнє завдання:
Конспект лекції № 20.
Тема: «Ознаки збіжності рядів з невід’ємними членами.»
План лекції № 20.
-
Визначення числового ряду з невід’ємними членами .
-
Ознаки (достатні умови) збіжності рядів з невід’ємними членами.
Ряд
![]() називається знакододатним (додатним),
якщо
називається знакододатним (додатним),
якщо
![]() .
Для таких рядів найпростіше розв‘язується
питання про збіжність ряду.
.
Для таких рядів найпростіше розв‘язується
питання про збіжність ряду.
Лемма 1. Якщо члени ряду невід’ємні, то він збігається тоді та тільки тоді, коли його часткові суми обмежені зверху. (доведення розібрати.)
Теорема 1(інтегральна ознака Коші збіжності ряду).
Якщо
функція ƒ невід’ємна та спадає на полу
прямій х ≥ 1, то для того, щоб ряд
![]() збігався, необхідно та достатньо, щоб
збігався інтеграл
збігався, необхідно та достатньо, щоб
збігався інтеграл
![]() .
.
Приклад.
Дослідити збіжність узагальненого
гармонійного ряду
![]() .
.
Розв‘язання.
Застосуємо інтегральну ознаку, поклавши
![]() .
Ця функція задовольняє всім умовам
теореми. Розглянемо інтеграл
.
Ця функція задовольняє всім умовам
теореми. Розглянемо інтеграл
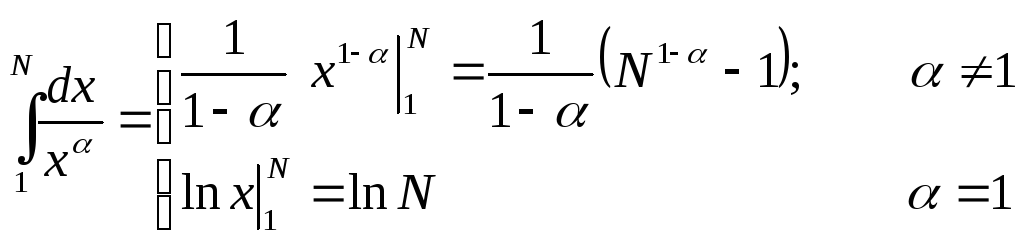 .
.
Прямуючи
![]() до нескінченності, з‘ясуємо збіжність
невласного інтегралу в різних випадках.
до нескінченності, з‘ясуємо збіжність
невласного інтегралу в різних випадках.
-
При
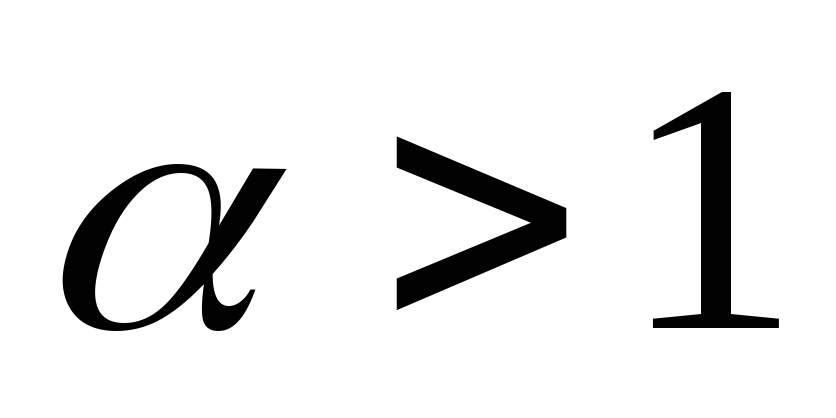 буде:
буде:
 ;
;
![]() .
.
Отже,
при
![]() невласний інтеграл скінчений і за
теоремою ряд збігається.
невласний інтеграл скінчений і за
теоремою ряд збігається.
-
При
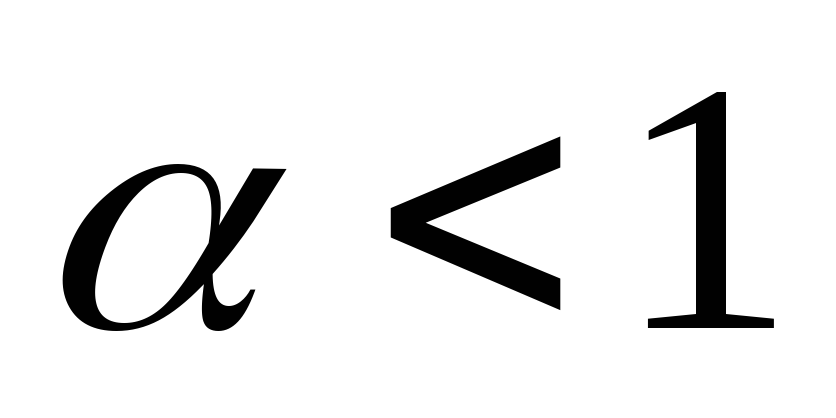 буде:
буде:
![]()
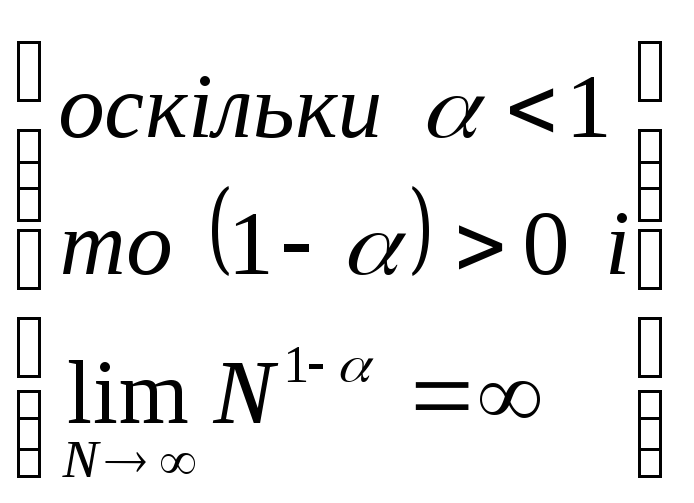
![]() ;
;
![]() .
.
Отже,
при
![]() невласний інтеграл розбігається,
значить, розбігається і досліджуваний
ряд.
невласний інтеграл розбігається,
значить, розбігається і досліджуваний
ряд.
-
При
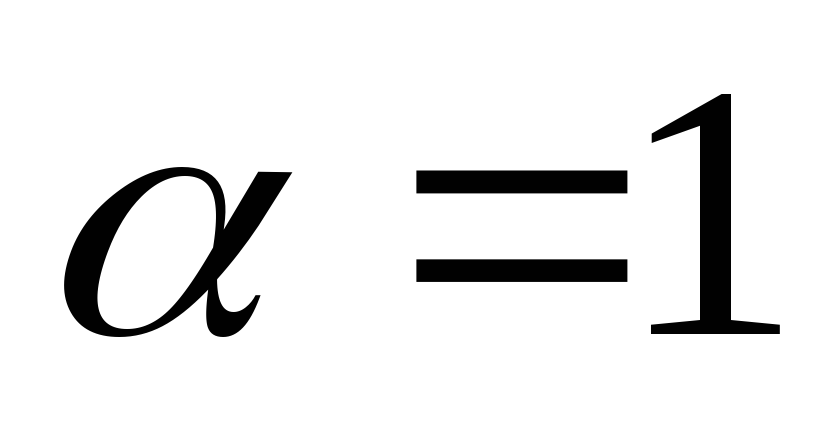 :
:
![]() ;
;
![]() .
.
Таким
чином, узагальнений ряд
![]() збігається при
збігається при
![]() і розбігається при
і розбігається при
![]() .
.
Теорема
2 (ознака
зрівняння.) Нехай
![]() ;
тоді:
;
тоді:
-
якщо ряд
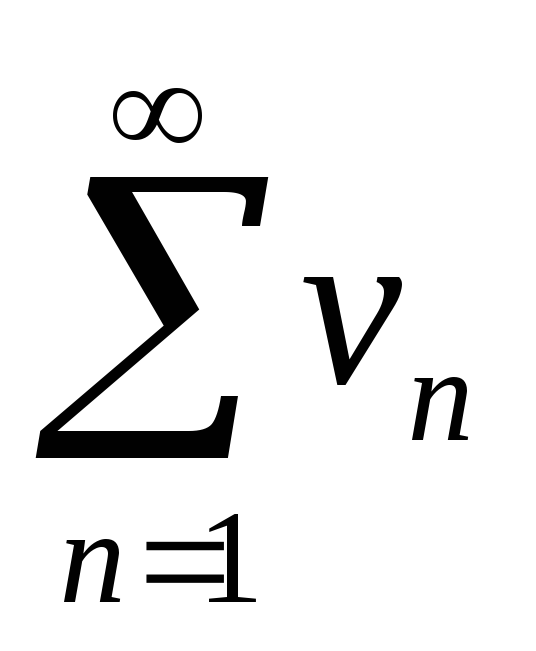 збігається, то й ряд
збігається, то й ряд
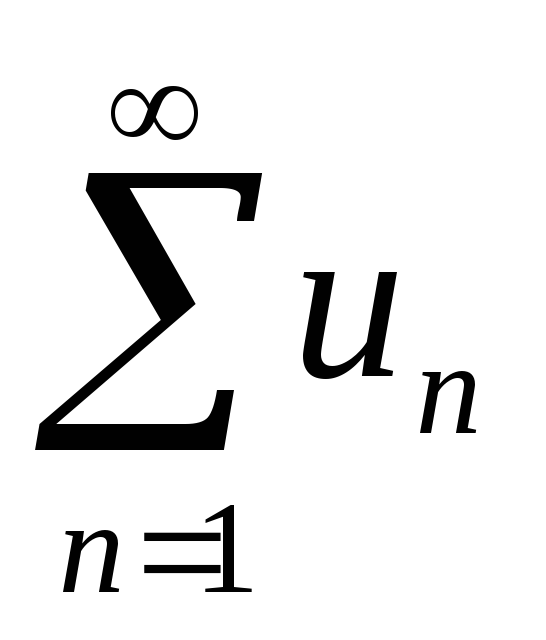 збігається;
збігається; -
якщо ряд
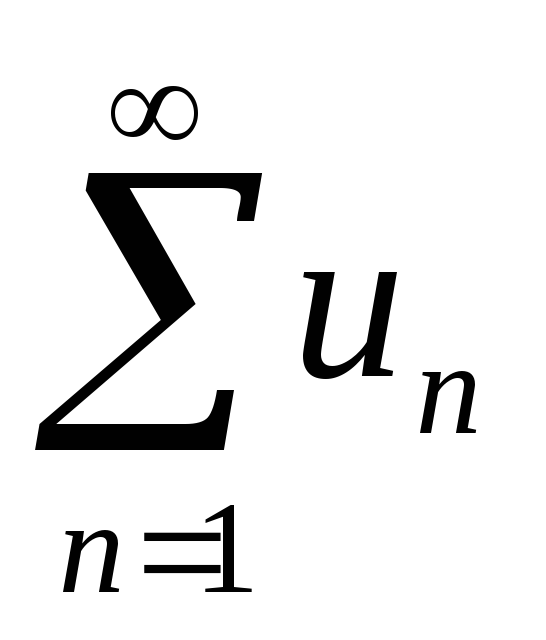 розбігається, то й ряд
розбігається, то й ряд
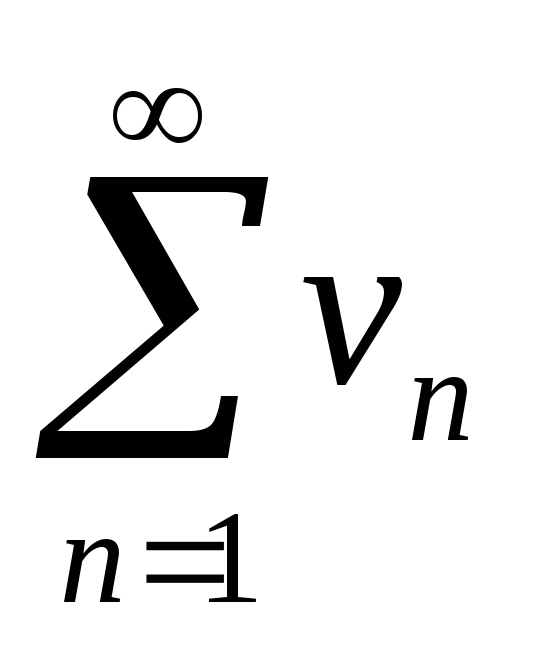 розбігається.
розбігається.
Приклад.
Дослідити збіжність ряду
![]() .
.
Розв‘язок.
Порівняємо цей ряд із збіжним геометричним
рядом
![]() (його знаменник
(його знаменник
![]() ).
Очевидно,
).
Очевидно,
![]() ,
а звідси випливає, що досліджуваний ряд
також є збіжним.
,
а звідси випливає, що досліджуваний ряд
також є збіжним.
Терема
3
(асимптотичне зрівняння).
Нехай
![]() та
та
![]() ;
тоді:
;
тоді:
-
якщо ряд
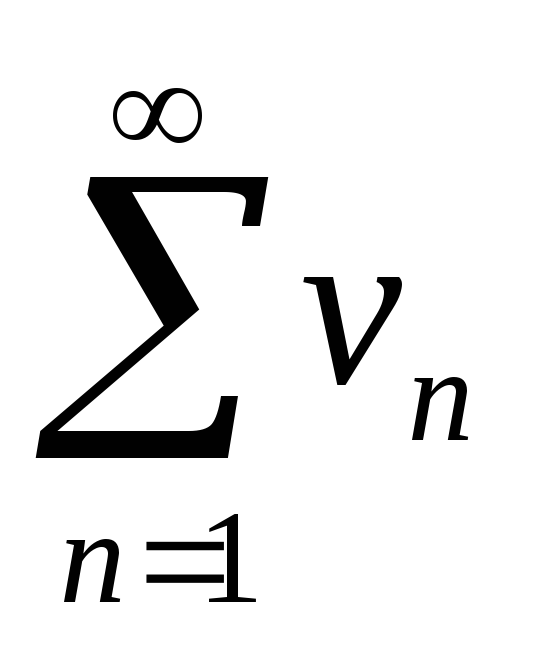 збігається та 0 ≤ l < +∞, то збігається
й ряд
збігається та 0 ≤ l < +∞, то збігається
й ряд
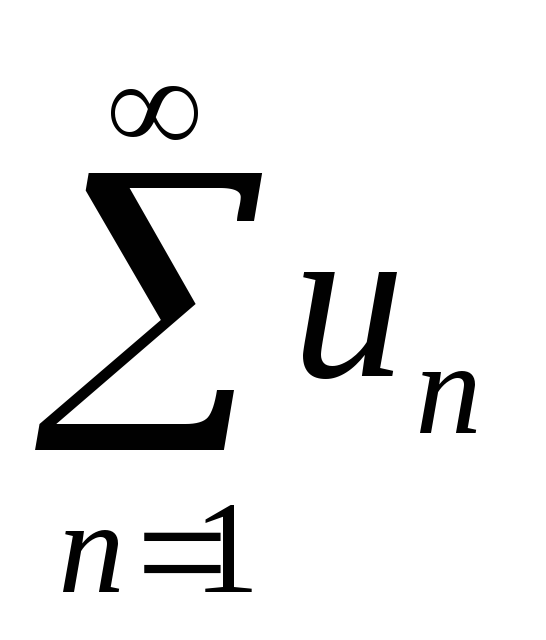 ;
; -
якщо ряд
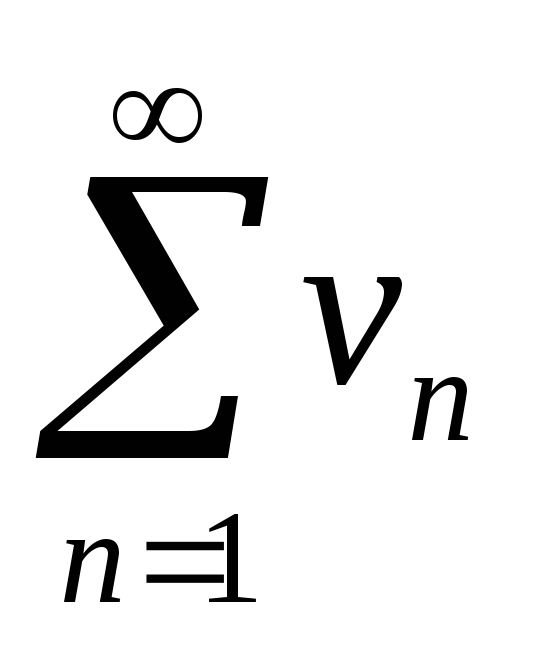 розбігається й 0 < l ≤ +∞, то розбігається
й ряд
розбігається й 0 < l ≤ +∞, то розбігається
й ряд
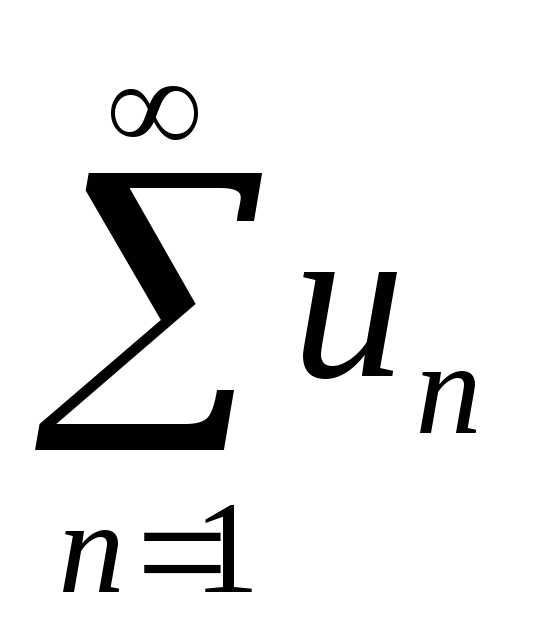 .
.
Якщо,
зокрема,
![]() ,
то ряди
,
то ряди
![]() та
та
![]() збігаються та розбігаються водночас.
збігаються та розбігаються водночас.
Приклад.
Дослідити збіжність ряду
![]() .
.
Розв‘язання.
Порівняємо досліджуваний ряд із збіжним
геометричним рядом
![]() :
:
 .
.
Оскільки
границя скінчена і не дорівнює нулеві,
а ряд
![]() збігається, то збігається і досліджуваний
ряд
збігається, то збігається і досліджуваний
ряд
![]()
Теорема
4
(ознака Д’Аламбера).
Нехай для ряду
![]() ,
,
![]() існує границя
існує границя
![]() .
Тоді, якщо k < 1, то ряд збігається, а
якщо k > 1, то ряд розбігається.
.
Тоді, якщо k < 1, то ряд збігається, а
якщо k > 1, то ряд розбігається.
Приклад
1.
Дослідити збіжність ряду
![]()
Розв‘язання.
Для досліджуваного ряду
![]() ;
;
![]()
![]() .
Отже, ряд збігається.
.
Отже, ряд збігається.
Приклад
2.
Дослідити збіжність ряду
![]() .
.
Розв‘язання.
![]() ;
;
![]()
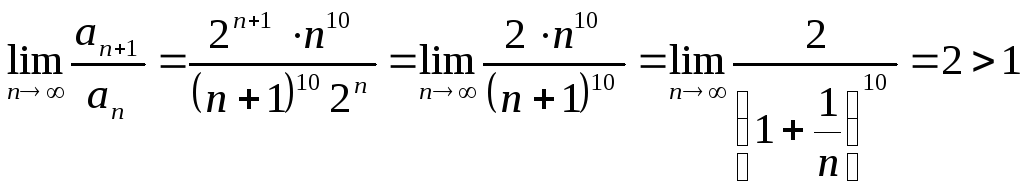 ,
отже ряд розбігається.
,
отже ряд розбігається.
Теорема
5
(ознака Коші).
Нехай для ряду
![]() ,
,
![]() існує границя
існує границя
![]() .
Тоді, якщо k < 1, то ряд збігається, а
якщо k > 1, то ряд розбігається.
.
Тоді, якщо k < 1, то ряд збігається, а
якщо k > 1, то ряд розбігається.
Приклад.
Дослідити збіжність ряду
![]() .
.
![]() ;
;
![]() .
Ряд є збіжним.
.
Ряд є збіжним.
З’ясувати за допомогою ознак збіжності, чи буде збіжним числовий ряд.
Загальний
член ряду задається формулою
![]() .
Це неправильна дробово-раціональна
функція (степінь числівника не менший
за степінь знаменника), отже, доцільно
скористатися необхідною умовою збіжності.
.
Це неправильна дробово-раціональна
функція (степінь числівника не менший
за степінь знаменника), отже, доцільно
скористатися необхідною умовою збіжності.
![]() . За необхідною умовою збіжності ряд
розбігається.
. За необхідною умовою збіжності ряд
розбігається.
-
 .
.
Степінь
числівника
![]() більший за степінь знаменника
більший за степінь знаменника
![]() , отже,
доцільно скористатися необхідною умовою
збіжності.
, отже,
доцільно скористатися необхідною умовою
збіжності.
![]() . Ряд розбігається.
. Ряд розбігається.
![]() не
існує, отже, за необхідною умовою
збіжності ряд розбігається.
не
існує, отже, за необхідною умовою
збіжності ряд розбігається.
Загальний
член ряду є правильною дробово-раціональною
функцією (степінь числівника менший за
степінь знаменника), числівник
еквівалентний величині
![]() , знаменник –
, знаменник –
![]() ,
отже,
,
отже,
![]() ~
~![]() .
.
Порівняємо
досліджуваний ряд з розбіжним гармонійним
рядом
![]() .
.
![]() .
.
Згідно
з граничною ознакою порівняння
досліджуваний ряд
![]() також є розбіжним.
також є розбіжним.
Скористаємося граничною ознакою порівняння . Оберемо допоміжний ряд.
![]() ~
~![]() ~
~![]() ;
;
![]() ~
~![]() ;
;
![]() ~
~![]() .
.
Таким
чином,
![]() ~
~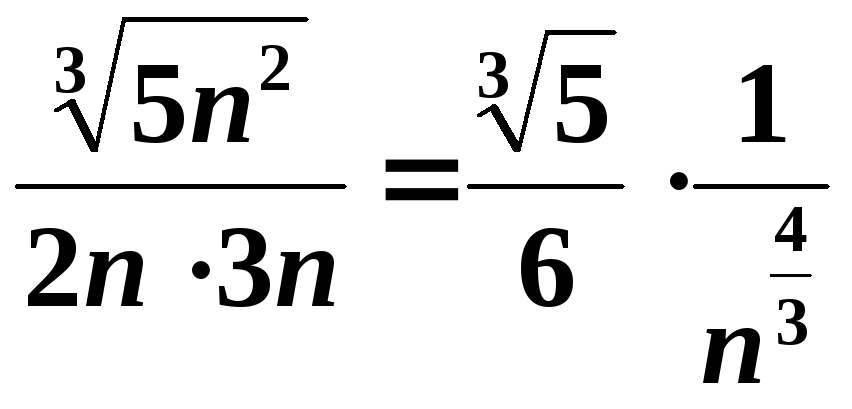 .
.
Порівняємо
досліджуваний ряд з узагальненим
гармонійним рядом
 , який є збіжним, оскільки показник
степеня
, який є збіжним, оскільки показник
степеня
![]() .
.
![]()
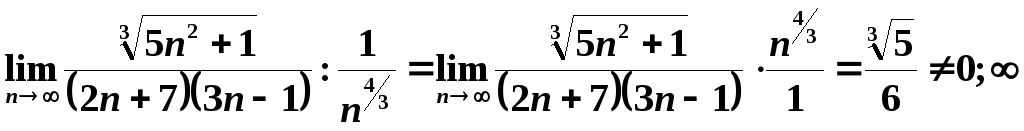 .
.
Згідно
з граничною ознакою порівняння ряд
![]() також збігається.
також збігається.
Загальний член ряду містить арксинус нескінченно малого аргументу, отже, за допомогою граничної ознаки порівняння можна щонайменше позбутися оберненої тригонометричної функції.
Скористаємося
наслідком першої важливої границі
![]() та оберемо ряд для порівняння.
та оберемо ряд для порівняння.
![]() ~
~
![]() ~
~
![]() .
.
Порівняємо
досліджуваний ряд з узагальненим
гармонійним рядом
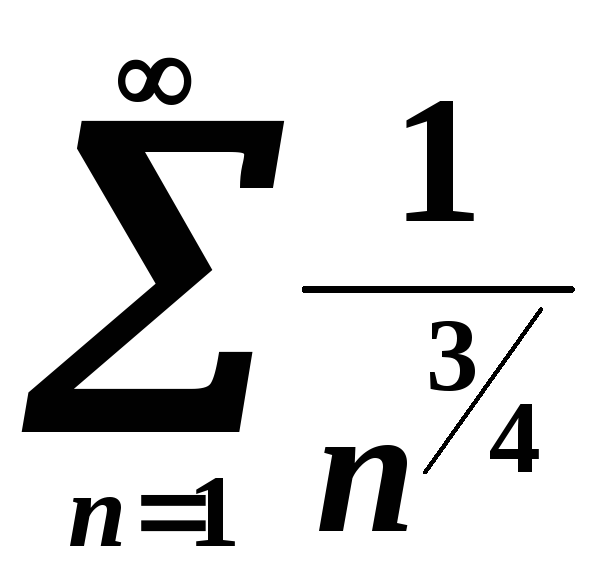 , який є розбіжним, оскільки показник
степеня
, який є розбіжним, оскільки показник
степеня
![]() .
.
![]()
 .
.
Згідно
з граничною ознакою порівняння
досліджуваний ряд
![]() також розбігається.
також розбігається.
-
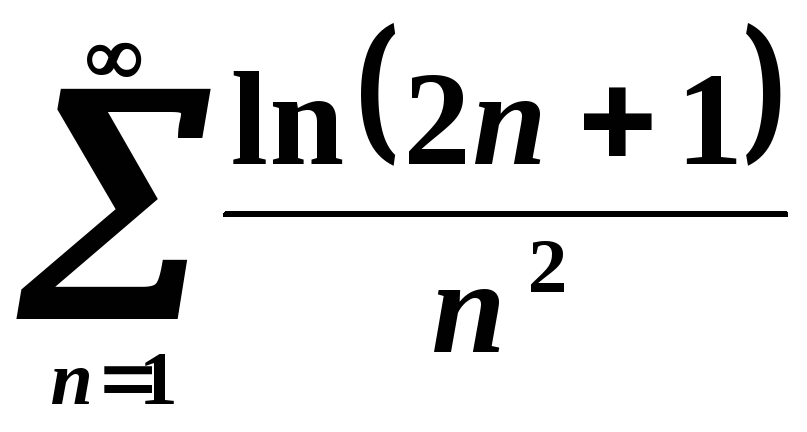 .
.
Скористаємося тим, що для досить великих значень змінної логарифм степеневої функції буде меншим за будь-який додатний степінь.
![]() ;
;
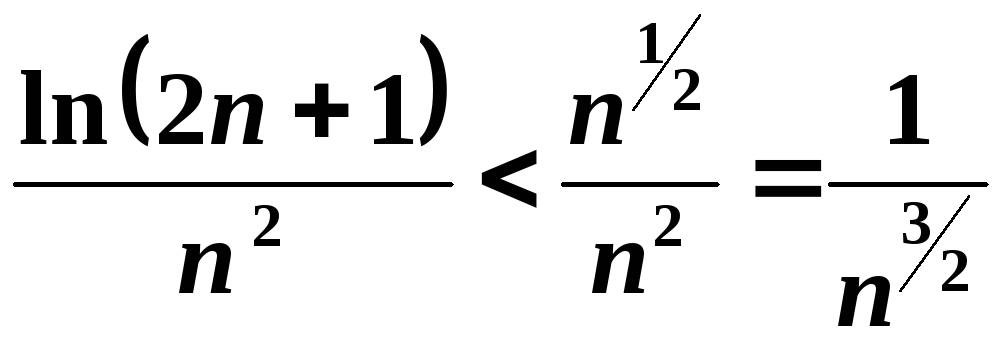 .
.
Ряд
 збігається, оскільки показник степеня
збігається, оскільки показник степеня
![]() ,
отже, згідно з ознакою порівняння ряд
,
отже, згідно з ознакою порівняння ряд
![]() також
буде збіжним.
також
буде збіжним.
Скористаємося тим, що для досить великих значень змінної логарифм степеневої функції буде більшим за одиницю.
![]() ;
;
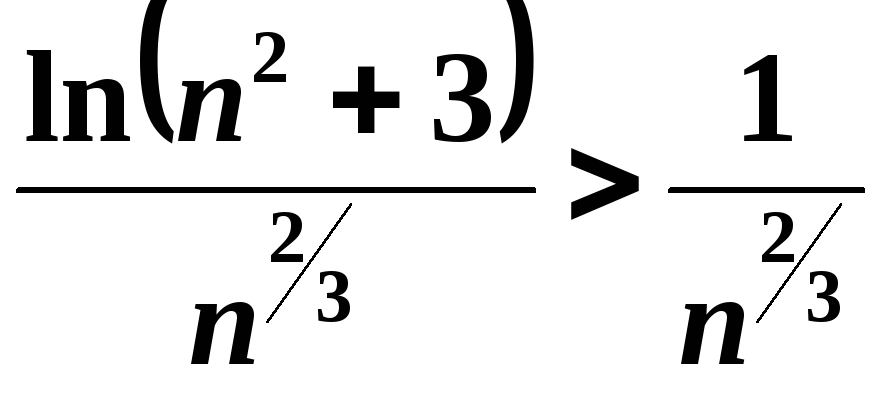 .
.
Ряд
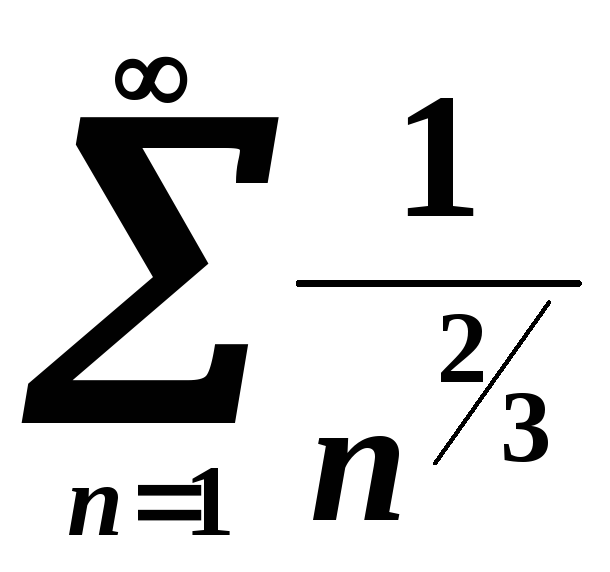 розбігається, оскільки показник степеня
розбігається, оскільки показник степеня
![]() ,
отже, згідно з ознакою порівняння ряд
,
отже, згідно з ознакою порівняння ряд
![]() також
буде розбіжним.
також
буде розбіжним.
Зауваження.
Якщо логарифмічна функція розташована
у знаменнику, для її оцінювання доцільно
скористатися нерівністю
![]() .
.
До загального члена ряду входить показникова функція, отже, можна використати признак Даламбера.
![]() ,
,
![]() .
.
![]() .
.
За ознакою Даламбера ряд збігається.
Побудуємо
формулу загального члена ряду. Числівники
дробів є факторіалами чисел
![]() ,
які складають арифметичну прогресію з
першим членом 1
та різницею 2,
тобто відповідають формулі
,
які складають арифметичну прогресію з
першим членом 1
та різницею 2,
тобто відповідають формулі
![]() .
Знаменники дробів є факторіальними
добутками, останні множники яких
обчислюються як
.
Знаменники дробів є факторіальними
добутками, останні множники яких
обчислюються як
![]() .
Тоді загальний член ряду має вигляд
.
Тоді загальний член ряду має вигляд
![]() . У цьому випадку також доцільно
скористатися ознакою Даламбера.
. У цьому випадку також доцільно
скористатися ознакою Даламбера.
![]()
![]()
![]()
![]()
![]() .
.
За ознакою Даламбера ряд розбігається.
Загальний член ряду є арктангенсом нескінченно малого аргументу, який містить факторіал, отже, скористаємося ознакою Даламбера.
![]() ,
,
![]() .
.
При
обчисленні
![]() використаємо наслідок першої важливої
границі
використаємо наслідок першої важливої
границі
![]() ,
тобто
,
тобто
![]() при
при
![]() .
.
![]()
![]()
![]()
![]()
За ознакою Даламбера ряд збігається.
Спроба
використати ознаку Даламбера для
дослідження наданого ряду призведе до
результату
![]() .
Скористаємося ознакою порівняння.
.
Скористаємося ознакою порівняння.
![]() .
.
Помітимо,
що кожен з множників буде більшим за
одиницю, отже, справджується нерівність
![]() .
.
Ряд
![]() буде розбіжним за необхідною умовою
збіжності
буде розбіжним за необхідною умовою
збіжності
![]() , тоді, згідно з ознакою порівняння,
досліджуваний ряд
, тоді, згідно з ознакою порівняння,
досліджуваний ряд
![]() також
буде розбіжним.
також
буде розбіжним.
Як
і у попередньому прикладі, ознака
Даламбера призведе до результату
![]() .
Знову скористаємося ознакою порівняння.
.
Знову скористаємося ознакою порівняння.
![]() .
.
Легко
помітити, що кожний з множників
![]() ,
,
![]() ,
,
![]() більший за одиницю.
більший за одиницю.
Тоді
![]() .
Гармонічний ряд
.
Гармонічний ряд
![]() розбігається, отже, за ознакою порівняння
ряд
розбігається, отже, за ознакою порівняння
ряд
![]() також буде розбіжним.
також буде розбіжним.
Загальний член ряду є степенево-показниковою функцією, отже, можна спробувати радикальну ознаку Коші.
![]()
![]() .
.
За радикальною ознакою Коші ряд розбігається.
Скористаємося радикальною ознакою Коші .
![]()
![]() .
.
За радикальною ознакою Коші ряд збігається.
Скористаємося
радикальною ознакою Коші . При обчисленні
![]() використаємо другу важливу границю
використаємо другу важливу границю
![]() .
.
![]()
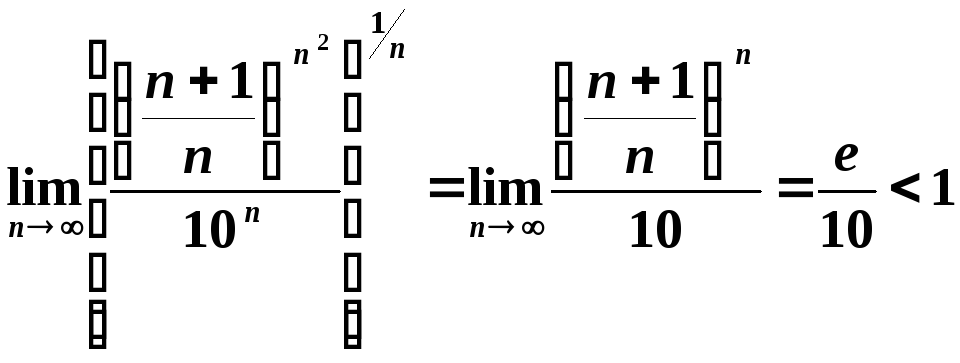 .
.
За радикальною ознакою Коші ряд збігається.
Спроба
використати радикальну ознаку Коші
призведе до результату
![]() .
Скористаємося необхідною умовою
збіжності.
.
Скористаємося необхідною умовою
збіжності.
![]() .
.
Ряд розбігається.
Загальний
член ряду задається за допомогою функції
![]() .
Ця
функція неперервного аргументу для
.
Ця
функція неперервного аргументу для
![]() набуває додатних значень та є спадною.
Обчислимо невласний інтеграл першого
роду від цієї функції та скористаємося
інтегральною ознакою Коші.
набуває додатних значень та є спадною.
Обчислимо невласний інтеграл першого
роду від цієї функції та скористаємося
інтегральною ознакою Коші.
![]()
![]()
![]() =
=
![]()
![]() .
.
Інтеграл є розбіжним, отже, ряд також розбігається.