матан 3 курс 2013 / лекции / Числові ряди / лекция № 19

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ЛЕКЦІЯ № 19

з теми: «Визначення ряду. Властивості збіжних рядів. Критерій Коші.»

Модуль КЗН-02.ПР.О.03.10 Числові ряди

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики. Протокол № ____ від _______20__ р. Голова циклової комісії ПМ Велікодна О. В.

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Визначення ряду. Властивості збіжних рядів. Критерій Коші.

Мета:

• Дидактична: розглянути поняття числового ряду, різновиди числових рядів. Вивчити поняття збіжності ряду та основні властивості збіжних рядів.

• Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.

• Методична: вдосконалювати методику проведення лекції з використанням методики проектної технології.

Тип: лекція

Вид: лекція з використанням проектної технології.

Методи та форми проведення заняття: мовні, пояснювально-ілюстративні, проблемно-пошукові, наочні.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

4. Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань: повторення основних понять та фактів щодо числових послідовностей.

3. Вивчення нового матеріалу:

• Тема лекції: Визначення ряду. Властивості збіжних рядів. Критерій Коші.

• Мотивація вивчення матеріалу: вивчити основні методи дослідження числових рядів для подальшого їх застосування як при розв’язанні математичних, так і прикладних задач.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

Конспект лекції № 19.

План лекції № 19.

1. Визначення числового ряду.

2. Властивості збіжних рядів.

3. Критерій Коші збіжності ряду.

Тема: «Визначення ряду. Властивості збіжних рядів. Критерій Коші.»

1. Визначення 1. Пара послідовностей 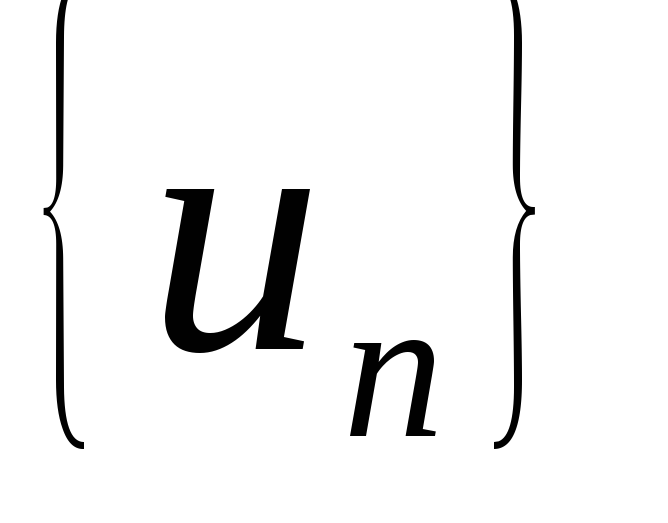та , де 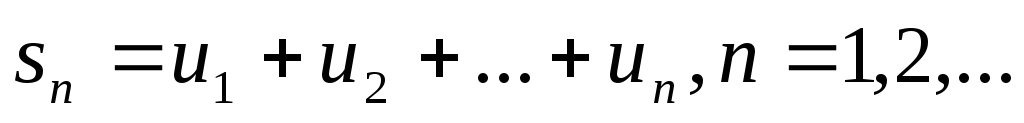називається рядом чи нескінченною сумою та позначається .

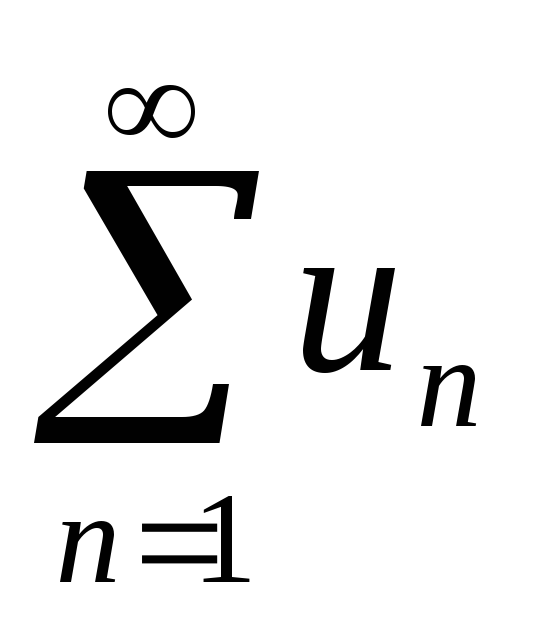Елементи послідовності називаються членами ряду, елементи послідовності - його частковими сумами.

Якщо існує скінчена границя , то вона називається сумою ряду. В цьому випадку ряд називається збіжним, та .

Якщо послідовність часткових сум не має скінченої границі, то ряд називається розбіжним.

Для ряду можна отримати наступне:

. З даних формул видно, що кожна послідовність та однозначно визначає іншу. Таким чином, щоб задати ряд, достатньо задати одну з послідовностей чи . В цьому випадку вивчення послідовностей рівносильне вивченню послідовностей.

Приклад 1. Ряд , де членами ряду є елементи геометричної прогресії є збіжним. Отже: . Далі . Отже, коли |q| < 1 ряд збігається та його сума є .

Приклад 2. Ряд, всі члени якого дорівнюють одиниці, тобто є розбіжним, так як .

2. Теорема (необхідна умова збіжності ряду). Якщо ряд збігається, то послідовність його членів є нескінченно малою. (Довести самостійно.)

Наприклад, - є збіжним, коли |q| < 1. . Якщо ж |q| ≥ 1, то , та ряд є розбіжним.

Теорема. Якщо ряди та збігаються, причому їх суми відповідно дорівнюють s´ та s´´, то при будь-яких λ´ та λ´´ ряд також збігається, та якщо s – його сума, то s = λ´s´ + λ´´s´´.

(доведення розібрати.)

Визначення 2. Для ряду ряд називається n-м залишком ряду. Якщо n-й залишок ряду збігається, то його суму будемо позначати .

Теорема. Якщо ряд збігається, то будь-який його залишок збігається. Якщо будь-який залишок ряду збігається, то сам ряд також збігається, причому, якщо , , , то при n = 1, 2, … . (доведення розібрати.)

Якщо ряд збігається, то його залишки є нескінченно малими.

3. Теорема (критерій Коші збіжності ряду). Для того, щоб ряд 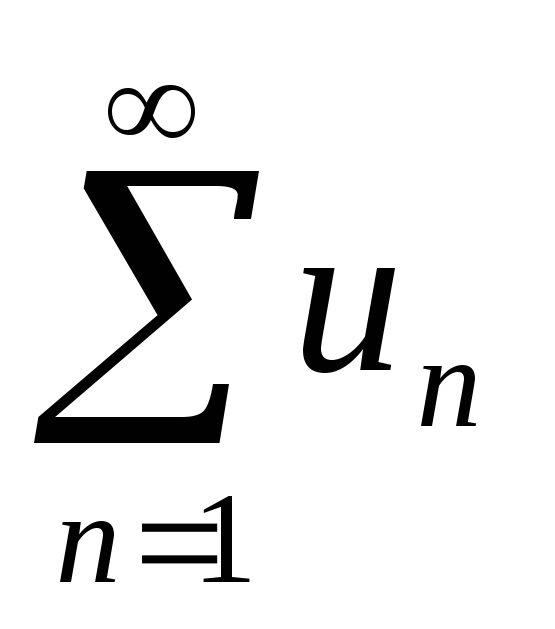збігався, необхідно та достатньо, щоб для будь-якого 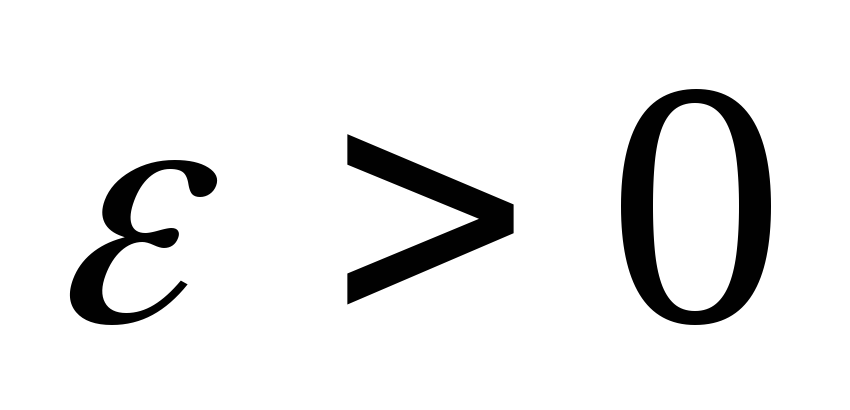існував такий номер 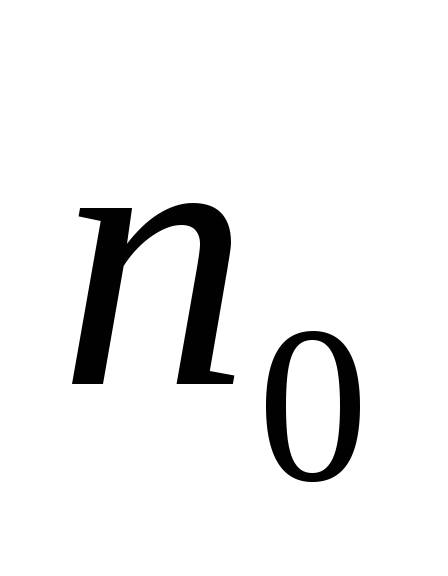, що для всіх 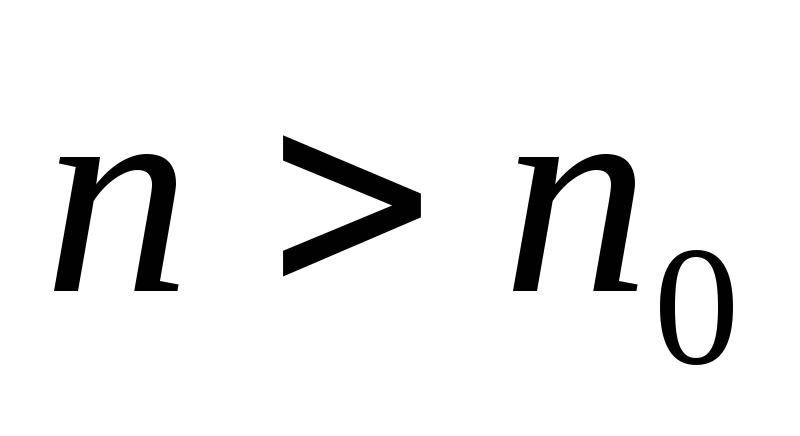та всіх цілих р ≥ 0 мало б місце

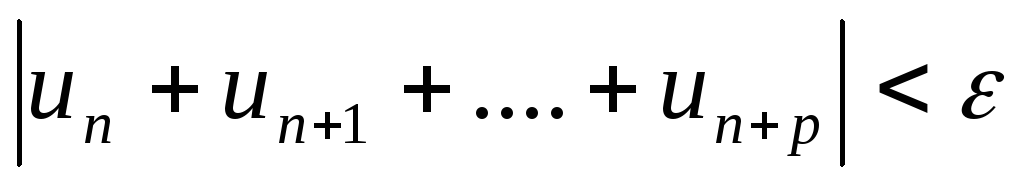
Приклади.

1. Скласти формулу загального члена 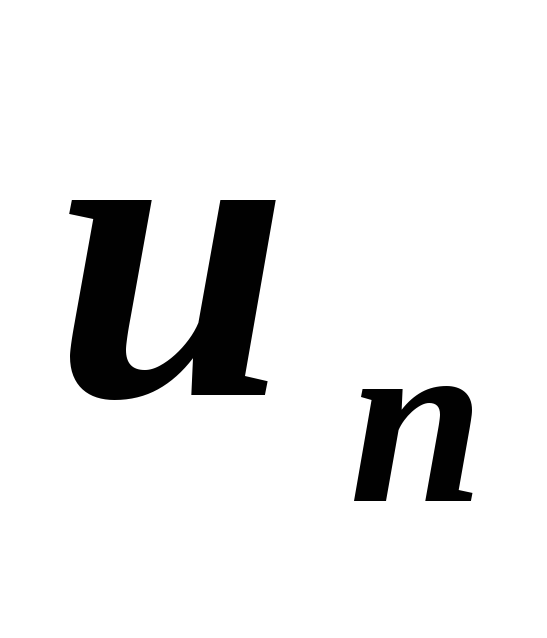та знайти 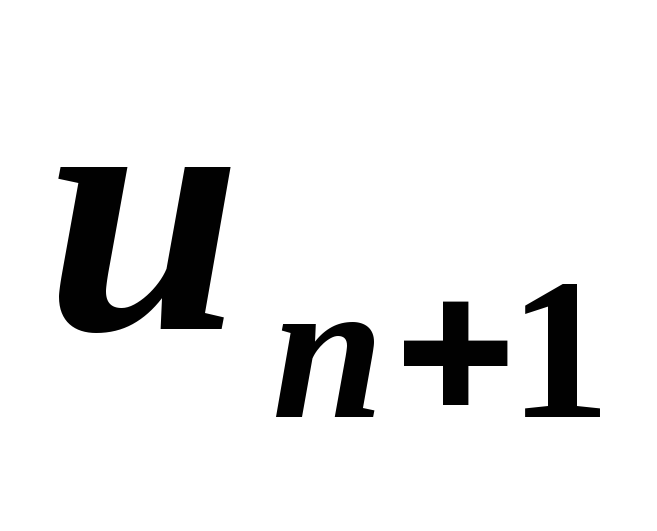для заданого числового ряду: 1)

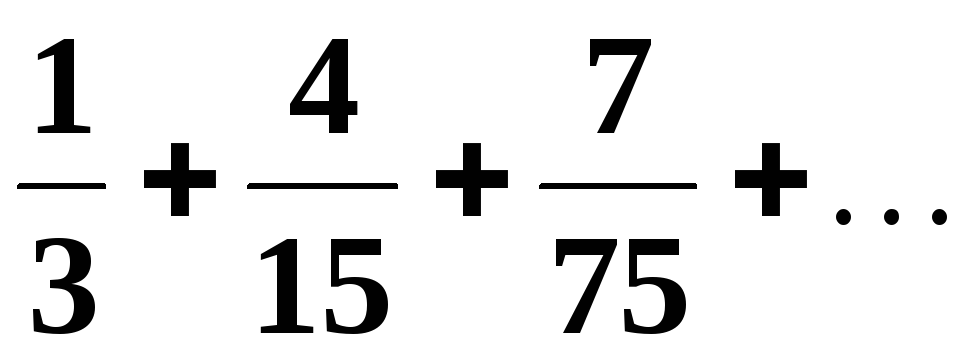
Члени ряду є дробами. Послідовність числівників складає арифметичну прогресію з першим членом 1 та різницею 3 , отже, задається з урахуванням формули загального члену арифметичної прогресії як = . Послідовність знаменників складає геометричну прогресію з першим членом 3 та знаменником 5 , отже, за формулою загального члену геометричної прогресії задається як . Таким чином, загальний член ряду задається рівністю .

Умову, яка задає , можна отримати з формули загального члена шляхом заміни змінної на , отже,

.

2)

Члени ряду є дробами. Числівник дробу складається з двох множників, перший з яких є факторіалом члена арифметичної прогресії з першим членом 1 та різницею 2 , отже, задається як . Послідовність других множників відповідає формулі . Знаменник кожного з дробів є добутком попереднього знаменника та нового множника, який складає з існуючими арифметичну прогресію з першим членом 2 та різницею 3 . Таким чином, послідовність нових множників відповідає формулі , а весь знаменник має вигляд . Таку послідовність будемо надалі називати факторіальним добутком. Отже, формулою загального члена ряду є рівність

.

Тоді .

Зауваження. Для факторіального добутку доцільно при побудові формули для підкреслити наявність всіх множників, які відповідають попередньому члену ряду.

2. З’ясувати за допомогою означення, чи буде збіжним числовий ряд, та за умови позитивної відповіді знайти суму ряду.

1. .

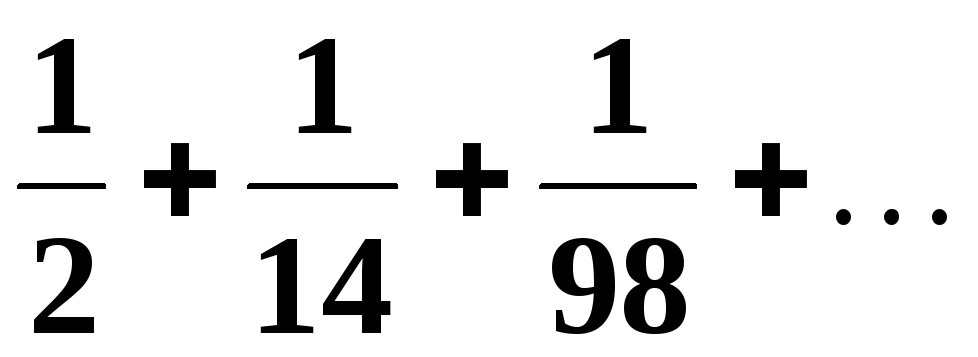Загальний член ряду задається формулою , отже, послідовність частинних сум має вигляд . Це сума членів геометричної прогресії з першим членом та знаменником , яка обчислюється за допомогою формули

.

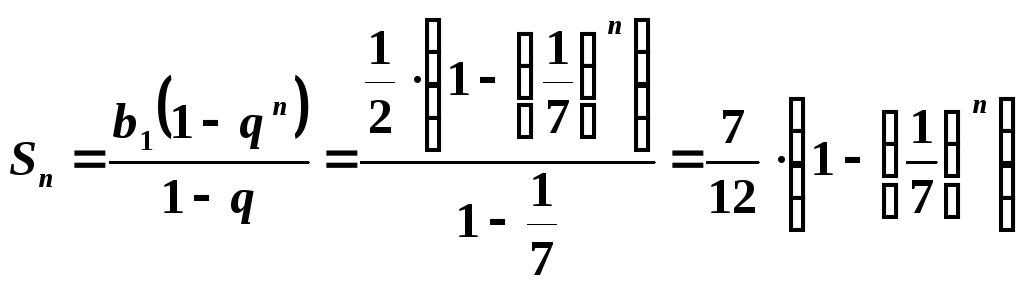Тоді , отже, ряд збігається, а його сума .

2) .

Загальний член ряду задається формулою , отже, послідовність частинних сум має вигляд

.

У дужках – сума членів арифметичної прогресії з першим членом 3 та знаменником 5 , отже, .

Тоді , тобто ряд є розбіжним.

3)

Загальний член ряду задається формулою , отже, послідовність частинних сум має вигляд

.

Легко помітити, що

,

,

,...

.

Тоді .

Отже, , ряд є збіжним, а його сума .