
4.224 4.225
4.226
![]() 4.227
4.227![]()
4.228
![]() 4.229
4.229![]()
4.230
![]() 4.231
4.231![]()
4.232
![]() 4.233
4.233![]()
4.234
![]() 4.235
4.235![]()
Если
![]() ,
,![]() ,
,![]() или
или![]() и при этом существует действительное
число
и при этом существует действительное
число![]() такое, что
такое, что![]() ,
(
,
(![]() ),
то
),
то![]() называетсябесконечно
большой функцией порядка
называетсябесконечно
большой функцией порядка
![]() относительно
относительно![]() .
.
В
задачах 4.236-4.241
определить порядок роста бесконечно
большой функции
![]() относительно
относительно![]() при
при![]() :
:
4.236
![]() 4.237
4.237![]()
4.238
![]() 4.239
4.239![]()
4.240
![]() 4.241
4.241![]()
В задачах 4.242-4.247 найти односторонние пределы:
4.242![]() .
4.243
.
4.243![]() .
.
4.244![]() .
4.245
.
4.245![]() .
.
4.246![]() .
4.247
.
4.247![]() .
.
§ 4. Непрерывность функций.
Если
функция
![]() определена всюду в некоторой окрестности
точки
определена всюду в некоторой окрестности
точки![]() (левой полуокрестности, правой
полуокрестности) и
(левой полуокрестности, правой
полуокрестности) и![]() (
(![]() ,
,![]() ),
то функция
),
то функция![]() называетсянепрерывной
в точке
называетсянепрерывной
в точке
![]() (непрерывной слева, непрерывной справа).
(непрерывной слева, непрерывной справа).
Каждая основная элементарная функция непрерывна в каждой внутренней точке своей области определения и непрерывна слева (справа) в крайней правой (крайней левой) точке области определения.
Если
в точке
![]()
![]() ,
то
,
то![]() называетсяточкой
разрыва
функции
называетсяточкой
разрыва
функции
![]() .
При этом различают следующие случаи:
.
При этом различают следующие случаи:
1)
Если
![]() ,
то
,
то![]() называетсяточкой
устранимого разрыва
функции
называетсяточкой
устранимого разрыва
функции
![]() .
.
2)
Если в точке
![]() функция
функция![]() имеет конечные односторонние пределы
имеет конечные односторонние пределы![]() и
и![]() ,
но они не равны друг другу, то
,
но они не равны друг другу, то![]() называетсяточкой
разрыва
1-ого рода.
называетсяточкой
разрыва
1-ого рода.
3)
В остальных
случаях
![]() называетсяточкой
разрыва
2-ого рода
.
называетсяточкой
разрыва
2-ого рода
.
Функция
![]() называетсянепрерывной
на отрезке
называетсянепрерывной
на отрезке
![]() ,
если она непрерывна в каждой его точке
(в точке
,
если она непрерывна в каждой его точке
(в точке![]() - непрерывна справа, в точке
- непрерывна справа, в точке![]() - непрерывна слева). Функция
- непрерывна слева). Функция![]() непрерывная на отрезке
непрерывная на отрезке![]() обладает свойствами:1)
ограничена на
обладает свойствами:1)
ограничена на
![]() ;2)
достигает на отрезке
;2)
достигает на отрезке
![]() своего наименьшего значения
своего наименьшего значения![]() и наибольшего значения
и наибольшего значения![]() ;3)
для любого числа
;3)
для любого числа
![]() ,
заключённого между числами
,
заключённого между числами![]() и
и![]() ,
всегда найдётся точка
,
всегда найдётся точка![]() такая, что
такая, что![]() ;4)
если
;4)
если
![]() ,
то всегда найдётся точка
,
то всегда найдётся точка![]() такая, что
такая, что![]() .
.
В
задачах 4.248-4.251 установить
при каком выборе параметров, входящих
в выражение функции, функция
![]() будет непрерывной.
будет непрерывной.
4.2484.249
4.250
![]() 4.251
4.251![]()
В задачах 4.252-4.269 определить точки разрыва функций и исследовать характер этих точек.
4.252
![]() 4.253
4.253![]()
4.254
![]() 4.255
4.255![]() 4.256
4.256 .
4.257
.
4.257
![]() 4.258
4.258![]() 4.259
4.259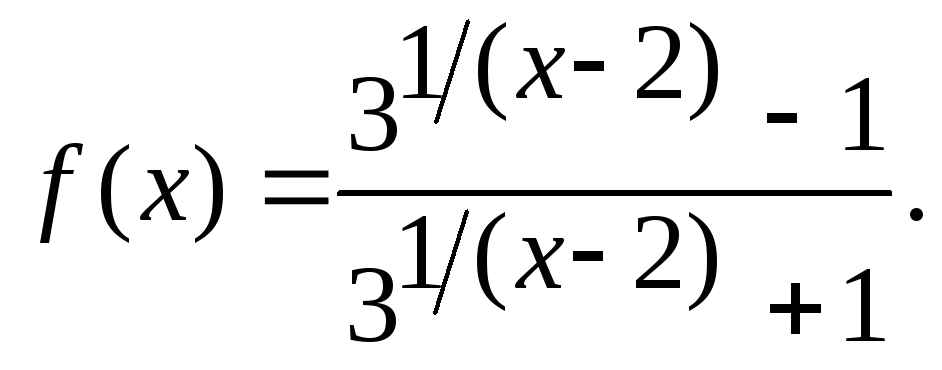
4.260
![]() 4.261
4.261![]()
4.262
![]() 4.263
4.263![]()
4.264
 4.265
4.265
4.266
 4.267
4.267
4.268
 4.269
4.269
4.270
Имеет ли корень уравнение
![]()
4.271
Имеет ли уравнение
![]() корни, принадлежащие отрезку
корни, принадлежащие отрезку![]()
4.272
Дана функция на отрезке
![]()
![]() Существует ли на этом отрезке точка,
в которой
Существует ли на этом отрезке точка,
в которой![]()
4.273
Принимает
ли функция
![]() значение
значение![]() внутри отрезка
внутри отрезка![]()
4.274
Доказать,
что функция
![]() разрывна в точке
разрывна в точке![]() и, тем не менее, принимает на
и, тем не менее, принимает на![]() как наибольшее, так и наименьшее значения.
как наибольшее, так и наименьшее значения.
§ 5. Комплексные числа.
Комплексным
числом
называется число вида
![]() ,
где
,
где![]() ,
,![]() -действительные
числа, символ
-действительные
числа, символ![]() - мнимая единица, для которой
- мнимая единица, для которой![]() . Число
. Число![]() - называетсядействительной
частью
комплексного числа
- называетсядействительной
частью
комплексного числа
![]() ,
число
,
число![]() -мнимой
частью.
Множество всех комплексных чисел
обозначается
-мнимой
частью.
Множество всех комплексных чисел
обозначается
![]() .
.
Комплексное
число
![]() изображается на плоскости с системой
координат
изображается на плоскости с системой
координат![]() (называемой комплексной плоскостью)
точкой, обозначаемой той же буквой
(называемой комплексной плоскостью)
точкой, обозначаемой той же буквой![]() и имеющей координаты
и имеющей координаты![]() .
.
Комплексное
число на комплексной плоскости
изображается также радиус-вектором
точки
![]() .
Длина радиус-вектора называетсямодулем
комплексного числа:
.
Длина радиус-вектора называетсямодулем
комплексного числа:
![]() ,
а угол его
,
а угол его![]() с осью
с осью![]() называетсяаргументом
комплексного числа:
называетсяаргументом
комплексного числа:
![]() ,
,![]() .
.
Аргумент
![]() комплексного числа вычисляют, как
правило, по формуле:
комплексного числа вычисляют, как
правило, по формуле: .
.
Комплексно-сопряжённым
числу
![]() называется число
называется число![]() .
.
Представление
комплексного числа выражением
![]() называется
алгебраической
формой
комплексного числа, выражением
называется
алгебраической
формой
комплексного числа, выражением
![]() -тригонометрической
формой и
выражением
-тригонометрической
формой и
выражением
![]() - егопоказательной
формой.
- егопоказательной
формой.
Арифметические
действия
(сложение, вычитание, умножение) над
комплексными числами в алгебраической
форме
выполняют по правилам действий над
многочленами, с учётом того, что
![]() :
:
![]() ;
;
![]() .
.
Деление комплексных
чисел выполняют по формуле:
![]() .
.
Умножение и деление комплексных чисел в тригонометрической форме выполняют по формулам:
![]() ;
;
![]() .
.
Умножение и
деление комплексных чисел в показательной
форме выполняют по формулам:![]() ;
;![]() .
.
Возведение
комплексного числа
![]() в натуральную степень
в натуральную степень![]() выполняют, используяформулу
Муавра:
выполняют, используяформулу
Муавра:
![]() .
.
Извлечение корня
![]() -ой
степени из комплексного числа
-ой
степени из комплексного числа![]() (не равного нулю) выполняют по формуле:
(не равного нулю) выполняют по формуле:
![]() ,
,
![]()
(здесь
![]() -
действительное положительное число).
Корень степени
-
действительное положительное число).
Корень степени![]() из комплексного числа имеет
из комплексного числа имеет![]() различных значений, расположенных на
комплексной плоскости на окружности
радиуса
различных значений, расположенных на
комплексной плоскости на окружности
радиуса![]() .
.
Алгебраическим
многочленом степени
![]() называется выражение вида:
называется выражение вида:
![]() ,
где
,
где![]() ,
,![]() -
некоторые числа (вообще говоря,
комплексные), называемые коэффициентами
многочлена, причём
-
некоторые числа (вообще говоря,
комплексные), называемые коэффициентами
многочлена, причём![]() .
.
Алгебраическим
уравнением
степени
![]() называется уравнение вида
называется уравнение вида
![]() Число
Число![]() ,
для которого
,
для которого![]() называетсякорнем
многочлена или уравнения.
называетсякорнем
многочлена или уравнения.
Теорема Безу.
Число
![]() является корнем многочлена
является корнем многочлена![]() тогда и только тогда, когда
тогда и только тогда, когда![]() делится на
делится на![]() ,
т.е. когда
,
т.е. когда![]() представляется в виде:
представляется в виде:![]() ,
где
,
где![]() - многочлен степени
- многочлен степени![]() .
.
Число
![]() называетсякорнем
кратности
называетсякорнем
кратности
![]() многочлена
многочлена
![]() ,
если
,
если![]() ,
где
,
где![]() .
.
Для многочленов имеет место следующая теорема:
Теорема Гаусса
(основная
теорема алгебры).
Всякий
многочлен ненулевой степени
![]() имеет ровно
имеет ровно![]() корней, если каждый корень считать ровно
столько раз, какова его кратность .
корней, если каждый корень считать ровно
столько раз, какова его кратность .
Всякий многочлен
![]() с действительными коэффициентами всегда
можно разложить в произведение линейных
и квадратичных (с действительными
коэффициентами) множителей.
с действительными коэффициентами всегда
можно разложить в произведение линейных
и квадратичных (с действительными
коэффициентами) множителей.
Всякий квадратный
многочлен с действительными коэффициентами
![]() на множестве комплексных чисел всегда
можно разложить в произведение только
линейных множителей:
на множестве комплексных чисел всегда
можно разложить в произведение только
линейных множителей:![]() ,
где корни
,
где корни![]() и
и![]() многочлена находятся по формулам:
многочлена находятся по формулам:
1)
если
![]() ,
то
,
то![]() - действительные;
- действительные;
2)
если
![]() ,
то
,
то![]() - комплексно-сопряжённые.
- комплексно-сопряжённые.
4.275. Изобразить на комплексной плоскости числа:
а)
![]()
![]() ;
;
б)
![]()
![]()
В задачах 4.276- 4.279 выполнить указанные действия, представив результат в алгебраической форме:
4.276
а)![]() ;б)
;б)![]() ;в)
;в)![]() .
.
4.277
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
4.278
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
4.279
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
В задачах 4.280- 4.283 представить в тригонометрической форме комплексные числа, заданные в алгебраической форме:
4.280
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
4.281
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
4.282
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
4.283
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
4.284 Вычислить:
а)
![]() ;
;
б)
![]()
В задачах 4.285-4.286 представить в показательной форме следующие комплексные числа:
4.285
а)
![]() ;б)
;б)![]() ;в)
;в)![]() .
.
4.286
а)
![]() ;б)
;б)![]() ;в)
;в)![]()
4.287
Данные числа
![]() представить в показательной форме и
выполнить указанные действия над ними:
представить в показательной форме и
выполнить указанные действия над ними:
а)
![]() ;
;
б)
![]()
В задачах 4.288-4.289 используя формулу Муавра, вычислить следующие выражения:
4.288
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
4.289
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)![]() .
.
4.290 Найти и изобразить на комплексной плоскости все корни 2-й, 3-й и 4-й степени из единицы.
В задачах 4.291-4.293 найти все значения корней:
4.291
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
4.292
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
4.293
а)
![]() ;
б)
;
б)![]() ;в)
;в)![]() .
.
В задачах 4.294-4.296 найти все корни следующих алгебраических уравнений на множестве комплексных чисел:
4.294
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
4.295
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
4.296
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
