Интервальные оценки параметров распределения

Точечной называют оценку параметров распределения, которая выражается одним числом, например, среднее арифметическое является точечной оценкой математического ожидания, статистическая дисперсия является точечной оценкой дисперсии. Точечные оценки могут сильно отличаться от оцениваемого параметра при небольших объемах выборки. Поэтому при небольших объемах выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяет интервал, внутри которого находится оцениваемый параметр распределения.

Интервальные оценки математического ожидания

Пусть для выборки объема признакаполучены среднее арифметическоеи статистическая дисперсия. Зададим промежуток длиныс серединой в точкеи найдем вероятностьтого, что неизвестное математическое ожиданиерасположено внутри интервала, т.е. найдем

. (9)

Промежуток называетсядоверительным интервалом.

Промежуток называетсяточностью среднего арифметического.

Величина называетсядоверительной вероятностью или надежностью среднего арифметического.

Здесь возникают три задачи в математической статистике

1)построение доверительного интервала для по заданной надёжности :

2) определение – надёжности оценки математического ожиданияпри заданной точности,

3) определение минимального количество опытов , обеспечивающих необходимые надёжностьи точностьпри оценке.

Задача о надежности определения математического ожидания при заданной точности

1. Пусть объем выборки велик, например . В этом случае, в соответствии с теоремой Ляпунова среднее арифметическое как сумма большого числа случайных величин будет распределено приближенно нормально. Действительно, среднее выборочноеможно рассматривать как случайную величину, равную суммеслучайных величин. Выборочные значенияможно рассматривать как значения одинаково распределенных случайных величинс одним и тем же математическим ожиданиеми одной и той же дисперсией(Значенияизменяются от выборки к выборке). Найдем математическое ожидание и дисперсию среднего арифметического

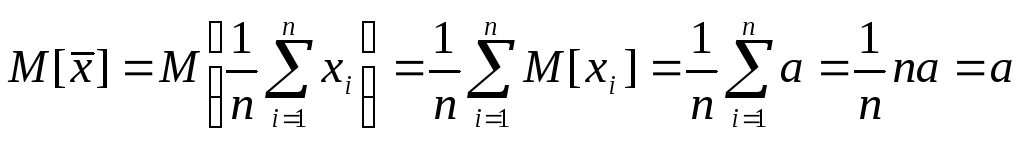. (10)

Найдем дисперсию среднего арифметического

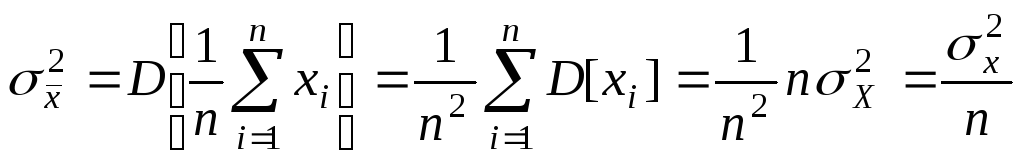(11)

Следовательно, дисперсия среднего арифметического в раз меньше статистической дисперсии самой случайной величины. Отсюда среднеквадратичное отклонение среднего выборочного равно.

Среднее арифметическое при больших значениях имеет нормальное распределение, Следовательно,

. (12)

где 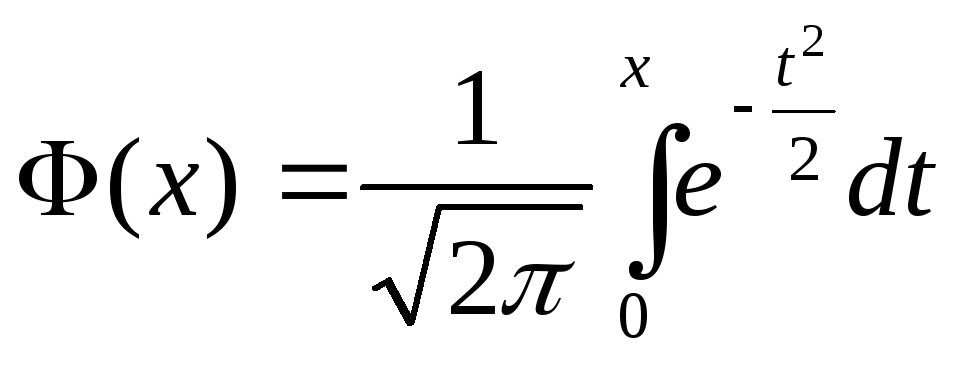– функция Лапласа, Следовательно,– оценкас точностьюи с надежностью, т.е. с вероятностьюнеизвестное математическое ожиданиенаходится в интервале.

Формулу (12) используют тогда, когда известна дисперсия случайной величины. При больших объемах выборки можно заменить в формуле (12) на .

2). Пусть объем выборки невелик (). В этом случае уже нельзя предположить, что среднее арифметическое распределено нормально. Английский статистик Госсет, писавший под псевдонимом Стьюдент, нашел закон распределения случайной величины– центрированного и нормированного среднего арифметического. Плотность этого распределения имеет вид

, (13)

где ,число степеней свободы.

Отметим, что в некоторых изданиях плотность распределения обозначается. Распределение Стьюдента зависит только от числа степеней свободыи не зависит от неизвестных параметров. Эта особенность является его большим преимуществом.

Распределение Стьюдента близко к нормальному при больших значениях (практически при). Пусть задан интервал. Вычислимс помощью распределения Стьюдента. Если,то . Следовательно,

, Здесь было учтено, что является четной функцией. Для функции, где, существуют подробные таблицы. По заданной надежностии объему выборки по таблицам находится значение, отсюда определяется доверительный интервал для математического ожидания

При оценке математического ожидания с помощью среднего арифметического при большом значении часто пользуются правилом, которое позволяет грубо оценить интервал возможных значений математического ожидания.

. Отсюда и следовательно

.

Пример 1. Из очень большой партии деталей отобрано 72 детали. Их средний вес . Дисперсия. С какой вероятностью можно утверждать, что средний вес деталей всей партии не меньше 649 г и не больше 651 г.

Решение. Здесь ,,.

Считаем, что распределено нормально. Тогда.

Пример 2. Из очень большой партии цилиндрических деталей отобрано 10 деталей. Измерены диаметры деталей и найдено их среднее арифметическое . Дисперсия.Найти надежность того, что среднее значение диаметров всей партии заключено между 5.96 и 6.08 мм.

Решение. В данном случае объем выборки мал Поэтому нужно использовать распределение Стьюдента.

.