Метод Квайна - Мак-Класки

Совершенные нормальные формы записи логических функций дают однозначное представление логических функций, но иногда являются очень громоздкими. Поэтому для булевых функций, представленных в виде СДНФ или СКНФ, возникает задача минимизации.

Индексом простоты (или сложностью) булевой функции называется число , определенное на множестве всех ДНФ, тождественных функции и удовлетворяющее следующим свойствам:

1. Свойство неотрицательности: для число ;

2. Свойство монотонности: если 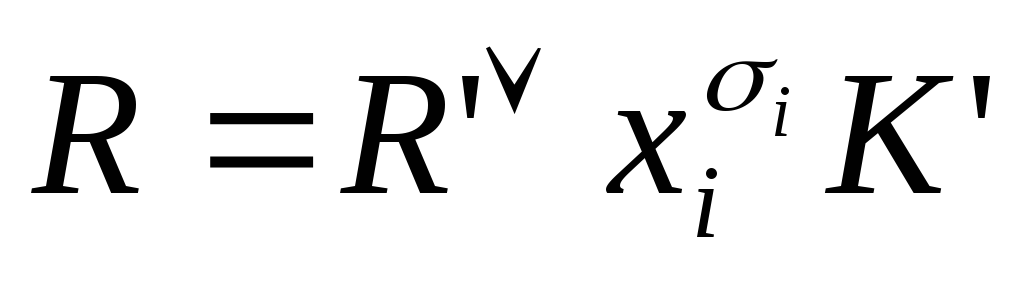, где – элементарная конъюнкция, то .

3. Свойство выпуклости: .

4. Свойство инвариантности: если ДНФ = получена из ДНФ = путем переименования переменных без отождествления, то .

Примеры выбора :

1) - число букв переменных, встречающихся в записи . Под буквой понимают символ переменной или ее отрицание, если переменная входит в формулу m раз, то говорят, что формула содержит m букв . Например в выражении число переменных равно 3, а число букв равно 5, т.е. число букв равно числу вхождений переменных.

2) - число элементарных конъюнкций, входящих в .

3) - число символов отрицаний, встречающихся в записи . Каждый из указанных индексов удовлетворяет перечисленным свойствам.

Иллюстрация: Пусть задана вектором состояний. Тогда для нее может быть записана СДНФ в виде

Эту функцию можно упростить

Вычислим индексы простоты для и .

, ;, ;

,.

Следовательно, проще для всех трех индексов простоты.

Задача минимизации заданной логической функции сводится к представлению ее дизъюнктивной (или конъюнктивной) нормальной формой, имеющей наименьший индекс простоты. В качестве индекса простоты наиболее часто используется индекс .

Минимизация булевых функций методом Квайна – Мак-Класки.

Импликантой функции называется конъюнкция некоторых аргументов из набора и их отрицаний, обладающая следующими свойствами:

1) Если на некотором наборе импликанта принимает значение 1, то и принимает на этом наборе значение 1.

2) При исключении хотя бы одного множителя из свойство 1) не выполняется.

Пример:

на наборах (0,0,0), (0,0,1), (0,1,1).

Рассмотрим . на наборах (0,0,0), (0,0,1). На этих наборах , т.е. выполняется условие 1). Если вычеркнуть один множитель из и оставить, например, , то. принимает значение 1 на наборах (0 0 0), (0 0 1), (0 1 0), (0 11), причем на выделенном наборе . Аналогичным образом , принимает значение 1, причем на выделенных наборах . Следовательно, при вычеркивании одного множителя у свойство 1) не выполняется. Это означает, что является импликантой функции.

Пусть на некотором наборе функция обращается в 1. Если на этом наборе импликанта функции обращается в 1, то говорят, что импликанта накрывает эту единицу функции .

Система импликант функции называется полной, если любая единица из таблицы значений функции накрывается хотя бы одной импликантой.

Сокращенной ДНФ функции называется дизъюнкция всех импликант из полной системы импликант.

Утверждение: Сокращенная ДНФ. функции совпадает с самой функцией.

Действительно, дизъюнкция всех импликант из полной системы импликант равна 1 на тех наборах, где равна 1 функция ( в соответствии с определением импликанты ) и равна нулю на тех наборах, где равна нулю функция, т.е. значения сокращенной д.н.ф. функции и функции совпадают.

Сокращенная д.н.ф. функции содержит меньшее число букв, чем СДНФ Однако, во многих случаях допускается дальнейшее сокращение числа букв за счет того, что некоторые из импликант могут поглощаться дизъюнкциями других импликант.

Система импликант функции называется приведенной, если эта система полна, а никакая ее часть не является полной системой импликант функции .

Тупиковой ДНФ называется дизъюнкция всех импликант, составляющих приведенную систему.

Тупиковая ДНФ- выражение, полученное из сокращенной ДНФ, дальнейшее упрощение которого невозможно в рамках ДНФ.

Минимальной ДНФ называется тупиковая ДНФ, состоящая из наименьшего числа букв.

Одна и та же сокращенная ДНФ может иметь несколько тупиковых ДНФ и несколько минимальных ДНФ.

Процесс минимизации сводится к следующим действиям:

• строится полная система импликант,

• строится приведенная система существенных импликант, из которых собирается сокращенная ДНФ,

• строятся тупиковые ДНФ,

• выбирается минимальная ДНФ;

т.е. решение задачи осуществляется в соответствии со схемой

Пример получения минимальной ДНФ.

Дано: . Построить минимальную ДНФ.

• Строим полную систему импликант.

• Получение сокращенной ДНФ основывается на законе склеивания . Из него следует, что можно склеивать или объединять минтермы, отличающиеся только одним сомножителем. Будем склеивать не минтермы, а наборы. Выпишем все наборы переменных, соответствующие минтермам, входящим в разложение функции, в столбик, разбивая их на группы так, чтобы в каждую группу входили наборы с одинаковым числом единиц.

N Груп пы	Наборы	набора	Номера состава склеенного набора (шаг 1)		Номера состава склеенного набора (шаг 2)
1	0010 *	2 *	2,3	001– *	2,3, 10,11	–01–
			2,10	–010 *	2,10, 3,11	–01–
2	0011 *	3 *	3,11	–011 *
	1001 *	9 *	9,11	10–1
	1010 *	10 *	9,13	1–01
	1100 *	12 *	10,11	101– *
			10,14	1–10
			12,13	110–
			12,14	11–0
3	1011 *	11 *
	1101 *	13 *
	1110 *	14 *

Проводим попарное склеивание наборов из соседних групп (для склеивания наборы должны отличаться на одну переменную).

При склеивании общие элементы сохраняются, а элементы, которыми различаются наборы, заменяются чертой (шаг 1).

Наборы, участвующие в склеивании, помечаются *. В результате образуется второй столбец, к которому также применяется операция склеивания (шаг 2). При этом склеивают наборы из соседних групп с одинаковым положением черточек.

Далее может образоваться 3-й столбец (в данном примере 3-й столбец не получился) и т.д. Процесс продолжается до тех пор, пока склеивание возможно.

Существенными импликантами функции будут наборы во всех столбцах, не участвующие в склеивании (не помеченные *).

, , , , , .

Сокращенная ДНФ , ее длина составляет 17 букв

• Следующий этап – построение тупиковой ДНФ.

Для этого нужно составить импликантную таблицу. Строки этой таблицы обозначены импликантами функции, а столбцы минтермами функции. Каждая импликанта является частью какого-нибудь дизъюнктивного члена в СДНФ и обращается в единицу на том же наборе, что и соответствующий минтерм. На пересечении строки, в которой записана импликант, и столбцов соответствующих минтермов, частью которых является импликанта, поставим крестики. Тупиковые формы являются дизъюнкциями тех импликант, которые накрывают все минтермы.

Чтобы построить тупиковую форму, нужно выбрать минимальное число строк, покрывающих крестиками все столбцы. Ясно, что в систему выбранных строк должны обязательно входить строки, содержащие плюсы, которые являются единственными в столбце. Такие строки называются базисными. Простые импликанты, стоящие в базисных строках, образуют ядро рассматриваемой функции. Обведем кружочками плюсы в строках, соответствующих этим импликантам. Из оставшихся импликант выбираем минимальное число таких, которые покрывают крестиками все свободные столбцы (т.е. те, которые не содержат ).

Короче: в таблице нужно выбрать такие строки, чтобы во всех столбцах был как минимум один плюс (т.е. были накрыты все столбцы) и при этом удаление хотя бы одной строки оставляло без плюса (не накрытым) какой-нибудь столбец; импликанты, образующие эти строки, составят тупиковую ДНФ.

Импликантная таблица:

	1	2	3	4	5	6	7	8
	0010	0011	1001	1010	1100	1011	1101	1110
–01–				+		+
10–1			+			+
1–01			+				+
1–10				+				+
110–					+		+
11–0					+			+

В нашем примере в тупиковую ДНФ обязательно должна входить строка , иначе первые два столбца не накрываются. Следовательно, первая строка является базисной, и импликанта образует ядро функции. При таком выборе автоматически накрываются еще два столбца, четвёртый и шестой.. Тупиковыми импликантами являются:

(8)

(11)

(11)

(11)

(11)

(11)

(11)

На рисунке изображены все тупиковые ДНФ:

• Среди всех тупиковых ДНФ выбираем ДНФ наименьшей длины (8):

Ответ: МДНФ имеет вид .