кривые второго порядка

Таким образом, гипербола лежит вне полосы шириной 2a, параллельной оси (OY ).

	50. Понятие эксцентриситета						c
	О п р е д е л е н и е	2.4. Отношение e =						называется эксцен-
							a
	триситетом гиперболы.
	У гиперболы всегда	e > 1 (так как c > a).
	Для точек правой ветви (рис. 2.5)				фокальные радиус-векторы r1, r2
	вычисляются следующим образом:
		r1 = ex + a .
		r2 = ex			−	a
	Для точек левой ветви
		r1 = −ex − a .
		r2 =	−	ex + a

60. Понятие директрисы О п р е д е л е н и е 2.5. Директрисами гиперболы называются

прямые, перпендикулярные фокальной оси и задаваемые уравнениями

x = −	a	,	x =	a
	e			e
(на рис. 2.5 это прямые (CD) и			(P Q)).

З а м е ч а н и е. Отношение расстояния от любой точки гиперболы до фокуса к расстоянию от той же точки до соответствующей директрисы

равно эксцентриситету гиперболы:
	r1	= e,	r2	= e.
	d1		d2

70. Касательная к гиперболе

Уравнение касательной к гиперболе в точке касания M0(x0, y0) имеет

вид

xxa20 − yyb20 = 1.

11

§ 3. Парабола

О п р е д е л е н и е 3.1. Параболой называется геометрическое место точек на плоскости, расстояние от которых до некоторой точки фокуса равно расстоянию до некоторой прямой директрисы (рис. 3.1).

Рис. 3.1

Рис. 3.2

3.1. Вывод уравнения параболы

Пусть M (x, y) некоторая точка параболы,

F фокус,

d ди-

ректриса. Опустим из точки

F

перпендикуляр на прямую d.

Точку

пересечения обозначим через

A.

Разделим отрезок

[AF ] пополам и се-

редину отрезка обозначим через

O. Проведем через точку O прямую,

перпендикулярную прямой (AF ). Получим ось

(OY ). В качестве оси

(OX) возьмем прямую

(AF ). Опустим из точки

M перпендикуляр

на прямую d и точку пересечения обозначим через

B (рис. 3.2).

Положим

|

AF

|

= p,

тогда

A

−

p

, 0!,

F

p

, 0!. Из определения

2

2

параболы следует, что

|M F | = |M B|.

(3.1)

Так как

M F

= v x

p

+ y2,

M B = x + p,

(3.2)

2

|

|

u

!

|

|

2

u

− 2

t

то, подставив (3.2) в (3.1), получим

= x + p.

v

x

p

2

+ y2

u

− 2

!

2

u

t

12

Возведем обе части уравнения в квадрат и приведем подобные слага-

емые, получим			!2					p2
x	−	p			+ y2 = x2 + px +					,
		2
							4
x2 − px +				p2					p2
						+ y2 = x2	+ px +				,
					4					4
		y2 − 2px = 0,
					y2 = 2px,					(3.3)

где параметр p есть расстояние от фокуса до директрисы. Уравнение (3.3) каноническое уравнение параболы.

3.2. Свойства параболы

10. Симметрия относительно оси (OX)

Пусть точка (x0, y0) принадлежит параболе. Тогда она удовлетворяет уравнению

y02 = 2px0.

Очевидно, что точка (x0, −y0) также удовлетворяет этому уравнению.

20. Фокальный радиус-вектор любой точки параболы (рис. 3.2)

равен

r = x + p2 .

30. Касательная к параболе (3.3) в точке касания (x0, y0) определяется уравнением

y· y0 = p · (x + x0).

Упражнения

№375. Составить простейшее уравнение эллипса, зная, что:

1)полуоси его соответственно равны 4 и 2;

2)расстояние между фокусами равно 6 и большая полуось равна 5;

	3)	большая полуось равна 10 и эксцентриситет	e = 0, 8;
			√
	4)	малая полуось равна 3 и эксцентриситет e =		2		;
			2
	5)	сумма полуосей равна 8 и расстояние между фокусами тоже равно 8.

13

Р е ш е н и е

x2

y2

1) Из условия задачи следует, что

+

= 1,

то есть уравнение

4

2

2

x2

y2

2

эллипса имеет вид

= 1.

+

4

16

то b2 = a2 − c2 = 52 − 32 = 16

2) Так как 2c = 6,

a = 5,

и уравне-

x2

y2

ние эллипса имеет вид

+

= 1.

25

16

c

3) Так как a = 10,

e = 0, 8

и

e =

, то c = 8

и, следовательно,

b2 = a2 − c2 = 100 − 64 = 36,

a

поэтому уравнение эллипса имеет вид

x2

+

y2

= 1.

100

36

√

e =

√

=

a2 − 9

,

4) Так как b = 3,

e =

2

и

a2 − b2

, то

1

поэтому

2

a

2

a2

a2 = 18 и уравнение эллипса имеет следующий вид

x2

y2

= 1.

+

9

18

5) Так как

a + b = 8, 2c = 8,

то

c = 4, b2 = (8 − b)2 − 16 и,

следовательно,

b = 3,

поэтому

a = 5 и уравнение эллипса имеет следу-

ющий вид

x2

+

y2

= 1.

15

9

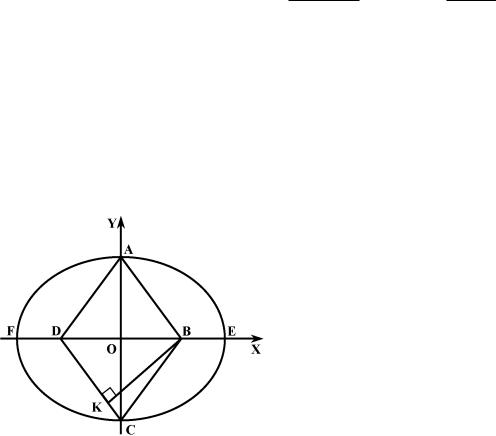
№ 379. Сторона ромба равна 5 и

высота 4, 8. Через две противолежа-

щие его вершины проходит эллипс,

фокусы которого совпадают с дву-

мя другими вершинами ромба. Со-

ставить уравнение эллипса, приняв

диагонали ромба за оси координат.

Р е ш е н и е

Пусть

ABCD ромб, |AB| = 5,

Рис. 3.3

[BK] [DC], |BK| = 4, 8, точки

A, C принадлежат эллипсу, точки

B, D его фокусы (рис. 3.3).

Рассмотрим BKC. Так

|CK|2 = |BC|2 − |BK|2, то

|CK|2 =

= 52 − (4, 8)2 = 2, 96

и, следовательно,

|CK| = 1, 4,

поэтому

|DK| =

14

= 5 − 1, 4 = 3, 6.
Рассмотрим	BKD. Так как |BD|2 = |DK|2 + |BK|2, то |BD|2 =
= −3, 62 + 4, 82	= 12, 96 + 23, 04 = 36	и, следовательно, |BD| = 6,
поэтому |OB| = 3 = c и |OA| = 4 = b.		Так как a2 = b2 + c2 = 42+

+32 = 25, то уравнение эллипса имеет вид

x2 y2

9+ 25 = 1.

№385. Определить эксцентриситет эллипса, зная, что:

1) малая ось его видна из фокуса под прямым углом (т. е.	1d	= 90 );
	B F2B2	0

2)расстояние между фокусами равно расстоянию между вершинами малой и большой осей;

3)расстояние между директрисами в четыре раза больше расстояния между фокусами.

Р е ш е н и е

Рассмотрим случай 2)

(рис. 3.4).

Так как 2c = |A1B1|

и

|A1B1|2 = a2 + b2,

то

a2 + b2 = 4c2. С другой

стороны, из определения эллипса следует, что

a2 − b2

= c2. Таким

образом, получили систему

a

b

= c

,

откуда

2a2 = 5c2 и,

a2

+ b2

= 4c2

2

−

2

2

5

2

u

c

u

u

2

5

u

5

t

c,

поэтому

e =

s

c

t

следовательно, a = v

= v .

2

Рис. 3.4

Рис. 3.5

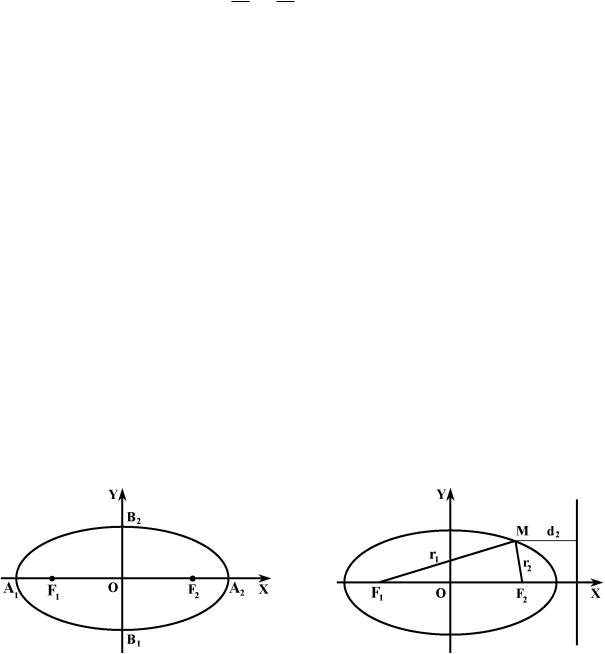
№ 394. На эллипсе, один из фокусов которого имеет координаты (+3; 0), взята точка M (+4; +2, 4). Найти расстояние этой точки до соот-

15

ветствующей директрисы, зная, что центр эллипса совпадает с началом координат.

Р е ш е н и е Для решения этой задачи (рис. 3.5) воспользуемся следующими фор-

мулами:

r1 = a + ex,

r2 = a − ex,

r1 + r2 = 2a, d2 =

r2

.

e

Так как r1 = |F1M | = √

= √

= 7, 4;

49 + 5, 76

54, 76

r2 = |F2M | = √

= √

= √

= 2, 6;

то

1 + 2, 42

1 + 5, 76

6, 76

a =

7, 4 + 2, 6

= 5; e =

a − r2

=

5 − 2, 6

=

2, 4

= 0, 6 и, следовательно,

2

x

4

4

d2 =

r2

=

2, 6

=

13

= 4

1

.

e

0, 6

3

3

№ 406. Найти уравнения тех касательных эллипса 3x2 + 8y2 = 45, расстояние которых от центра эллипса равно 3.

Р е ш е н и е

Пусть (x1, y1) точка касания. Очевидно, что уравнение касательной имеет вид 3x1 · x + 8y1 · y − 45 = 0. Из условия задачи следует, что

3 =	45		, откуда 3x12 =	225 − 64y2	. Так как точка (x1, y1)
	q9x12 + 64y12			3

лежит на эллипсе, то ее координаты удовлетворяют уравнению эллипса,

поэтому

225 − 64y12

+ 8y2

= 45,

откуда 225

−

64y2

+ 24y2

−

135 = 0 и,

3

1

1

9

1

225 − 64 ·

9

3

следовательно,

2

=

, y1 = ±

, а

2

=

4

= 9,

x1 = ±3,

y1

x1

4

2

9

поэтому мы получили четыре касательные, уравнения которых имеют

				3
		x
следующий вид:	±		± 8 ·	2				y − 1 = 0	или ±3x ± 4y − 15 = 0.
		5			45

№ 411. Вывести условие, при котором прямая Ax + By + C = 0 каса-

ется эллипса x2 + y2 = 1. a2 b2

16

				Р е ш е н и е
	Уравнение			касательной к эллипсу в	точке (x1, y1) имеет вид
x1	x +	y1	y = 1.	Так как Ax + By + C = 0	уравнение той же каса-
2		2
a		b

тельной, то коэффициенты при соответствующих переменных должны

x12

y12

x1 =

a2A

1

−

C

2

2

a

b

A

B

C

2

быть пропорциональны, поэтому

= = − , откуда

b B

y1 =

−

C

координаты точки касания. Так как точка (x1, y1)

лежит

на эллипсе,

то ее координаты удовлетворяют уравнению эллипса

x12

+

y12

= 1,

по-

a2

b2

a2A 2

b2B 2

C

C

этому выполняется следующее соотношение

−

+

−

= 1,

a2

b2

то есть

a2A2

+

b2B2

= 1, откуда

a2A2 + b2B2 = C2.

C2

C2

№ 422. Эллипс касается оси абсцисс в точке

A(+7; 0)

и оси ординат

в точке

B(0; +4). Составить уравнение эллипса, если известно, что оси

его параллельны осям координат.

Р е ш е н и е

Из условия задачи следует, что центр эллипса находится в точке (7; 4) (рис. 3.6), a = 7, b = 4, и, следовательно, уравнение эллипса имеет

следующий вид		(y − 4)2
(x − 7)2	+		= 0.
49		16

Рис. 3.6

Рис. 3.7

17

№ 437. Написать уравнение гиперболы, проходящей через фокусы эл-

	липса		x2	+		y2		= 1 и имеющей фокусы в вершинах этого эллипса.
		169			144
								Р е ш е н и е

Из уравнения эллипса следует, что вершинами эллипса являются точ-

ки (±13; 0) и (0; ±12), поэтому a = 13, b = 12

(рис. 3.7) и,

следо-

вательно, c2 = a2 − b2 = 132 − 122 = 25,

поэтому

c = 5.

Из условия задачи следует, что

a = c = 5, c = a = 13,

b2 = c2 − a2,

то есть b2 = 169 −25 = 144,

откуда

b = 12 и, следовательно, уравнение

x2

y2

гиперболы имеет вид

−

= 1.

25

144

№ 439 . Зная уравнения асимптот гиперболы

1

и одну из ее

y = ±

x

2

точек

√

составить уравнение гиперболы.

M (+12; +3

3),

Р е ш е н и е

Из

уравнения

асимптот

1

b

1

y = ±

x

следует,

что

= ±

,

откуда

2

a

2

a = ±2b. Подставим полученное выражение в уравнение гиперболы. По-

лучим x2 − y2 = 1. Так как точка M лежит на гиперболе, то ее коор-

4b2 b2

динаты удовлетворяют последнему уравнению, поэтому 122 − 27 = 1,

4b2 b2

откуда b2 = 9, и, следовательно, a2 = 36. Таким образом, уравнение

гиперболы имеет вид	x2		y2
		−		= 1.
	36		9

№ 443. Определить угол между асимптотами гиперболы, у которой: 1) эксцентриситет e = 2;

2) расстояние между фокусами вдвое больше расстояния между дирек-

трисами.

Р е ш е н и е

c

b

1) Так как

e =

,

b2 = c2 − a2,

то c2 = a2 + b2,

y = ±

x. Таким

a

a

образом, e = c = √

= v

!

2

b2 + a2

( b )2

+ 1 = 2, откуда

b

+ 1 = 4 и,

a

a

u

a

u a

t

18

следовательно,

b

!2

= 3,

то есть

b

=

±

√

,

поэтому

√

и

3

tg α =

3

a

a

±

√

√

√

3+√

√

3

o

k1 = 3, k2 = − 3. Так как tg ψ =

= − 3,

то

ψ = 120 .

1−3

a

a

2) Так как

2c = 2 · 2

,

то

c = 2

,

поэтому

c2

= 2a2,

то есть

e

c

a

π

b2 + a2 = 2a2,

откуда

b2 = a2,

и, следовательно, ψ =

.

2

№ 451. Найти точки пересечения гиперболы x2 − y2 = 1 со следую-

щими прямыми:

90 36

1) x −5y = 0; 2) 2x + y −18 = 0; 3) x −y + 5 = 0; 4) √10x −5y + 15 = 0. Р е ш е н и е

Рассмотрим случай 1).

x2

y2

= 1

25y2

y2

= 1

Нам надо решить систему

90

−

36

, откуда

90

−

36

x − 5y = 0

x = 5y

и, следовательно,

x = 10

y = ±2 .

±

и

−

−

.

получили две точки

Таким образом,

(10; 2)

(

10;

2)

№ 456. Написать

уравнение

прямой,

которая

касается

гиперболы

x2

y2

−

= 1 в точке

(+5; −4).

5

4

Р е ш е н и е

x · x1

y · y1

Уравнение касательной в точке (x1, y1) имеет вид

−

= 1,

откуда x + y = 1 и, следовательно,

x + y − 1 = 0.

5

4

№ 462. Гипербола касается прямой

x −y −2 = 0 в точке

M (+4; +2).

Составить уравнение этой гиперболы.

Р е ш е н и е

Уравнение касательной к гиперболе, проходящей через точку M ,

4

2

y = 1.

По

условию

задачи

касательная задается

имеет вид

x −

a2

b2

уравнением x−y −2 = 0. Так как это уравнения одной и той же прямой,

19

коэффициенты при соответствующих неизвестных должны быть пропор-

	4					2			1		4				2			1
					y2
циональны, поэтому	2									, откуда											и a2 = 8, b2 = 4,
	a			=				=						=				=
	1				1				2		a2					b2
																		2
											x2				y2
то есть уравнение гиперболы имеет вид													−				= 1.
											8				4

№ 464. Составить уравнение гиперболы, зная уравнения ее асимптот y = ±12 x и уравнение одной из ее касательных: 5x − 6y − 8 = 0.

Р е ш е н и е

Так как

1

b

1

y = ±

x

асимптоты, то

=

,

откуда

a = ±2b. Пусть

2

a

2

прямая

a касательная к эллипсу, тогда ее уравнение должно удовле-

x

y

= 0

5x

−

6y

8 = 0

5 − 6 − 8 2

,

откуда

− 2

,

творять системе x

x1

y

y1

8x1

8y1

·

·

= 1

x

y

8 = 0

−

a2

−

b2

−

a2

b2

x1

5

x1 =

5

=

a2

b2

8

2

то есть

или

. Подставим найденные значения

y1 = 3 b2

y1 = 3 b2

4

4

для x1

и

y1

и выражение a через b в уравнение гиперболы, получим

( 25 b2)2

( 43 b2)2

25

2

9

2

2

2

−

= 1,

откуда

b

−

b

= 1,

поэтому b

= 1,

a = 4

4b2

b2

16

16

и, следовательно, уравнение гиперболы имеет вид

x2

− y2 = 1.

4

№480. Составить уравнение параболы, зная, что:

1)расстояние фокуса от вершины равно 3;

2)фокус имеет координаты (+5; 0), а ось ординат служит директрисой;

3)парабола симметрична относительно оси x, проходит через начало координат и через точку M (+1; −4);

4)парабола симметрична относительно оси y, фокус помещается в точке (0; +2), и вершина совпадает с началом координат;

5)парабола симметрична относительно оси y, проходит через начало координат и через точку M (+6; −2).

20