сил хватает, что бы вывести или доказать. А если несколько лемм по маршруту – это значит ваше вы разбили доказательство на несколько частей. Значит вам до леммы надо дойти раз, а потом идти до теоремы.

Т – истинна, вы ведь выводите то, что доказуемо. Значит

С1& С2& ... &СJ&…& СN & T ≡ ИСТИНА и С1& С2& ... &СJ&…& СN & T ≡ ЛОЖЬ

Вы убеждены, что аксиомы истинные, а потом вы убеждены, что вы правильно действуете – но нет гарантии, что то что вы получили истинно. Это просто выводится, это просто доказуемо. Поэтому в математике истинной никто не занимается, истинной же занимаются в физике и в других науках, которые ближе к природе, а в математике выводят. Выводимость и истинность это разные свойства предложения. Поэтому если вы что-то вывели, это хорошо, но обязательно надо проверить на истинность. Физик-теоретик придумал закон, а физик-экспериментатор его проверяет. Ньютон придумал закон всемирного тяготения, а проверят ему и не пришлось, потому что он этот закон подсмотрел у другого. Только тот никак не мог догадаться, что там расстояние в квадрате. Так и Эйнштейн все эти законы у Лоренца списал, все эти законы Лоренц придумал. Лоренц сказал, что все зависит от геометрии, он все сказал что и Эйнштейн потом пересказал. Эйнштейн сказал, что Лоренц правильно сказал, но много, а самое главное, что среди высказываний Лоренца вот это правильное.

Вернемся к слайду. Вариант здесь разные приведены, когда я к цепочке приписал Т, как истину. И второй, когда приписал Т, как ложь. Прямое доказательство и от противного. Выбор осуществляется на любителя в математике, хотя в некоторых приложениях не на любителя. Например, в вычислительной технике, в автоматизации доказательств и практически все программы «от противного». Если посмотреть логически, то кажется все равно, доказывать что истина или доказывать что ложь. А с точки зрения программирования так лучше. Вы не сравнивайте человека и машину, потому что человек не возьмется за такую комбинаторику.

Лекция 7

ЛОГИКА ПРЕДИКАТОВ

Мы выяснили, что язык очень важен для теории. Языков очень много, очень разных. И вот очень популярный язык, который используется для построения формальных теорий и называется языком ЛОГИКИ ПРЕДИКАТОВ.

Вот если мы возьмем простое предложение, то там есть подлежащие и сказуемое. Логика предикатов – это на самом деле логика сказуемых. В простом предложении есть подлежащие и сказуемое, язык почему-то выделяет сказуемое и ставит его в цент все построений. И всякими добавками, выводами и т.д. дает вам инструмент для того, что бы вы построили практически любую формальную теорию. А сказуемое, потому что вы сказуете чего-то, причем вы сказуете о том, что под этим словом лежит (вот почему подлежащие). Назвать можно что угодно, а вот сказать надо то, что к месту сейчас и то, что важно. Вот вы назвали, а потом

сказали, вы могли сказать правильно, а могли и не правильно. Ложь не входит в то множество семантически правильных предложений. Если я буду проверять правильно я сказал или нет, я буду по сути дела проверят разные формулу, теоремы.

Ивы сказуете обычно о том, что у чего-то есть какое-то свойство – это является вашим базовым сказанием. «Сидоров высокий» например. Более нейтральное слово, которое можно использовать вместо «свойство», это «признак».

Иэтот признак распознавать надо. А вот что за система распознавания, которая скажет да или нет. Факт в том заключается, что распознавать приходиться постоянно.

От распознавания в искусственном интеллекте не уйдешь. Вам понадобятся знаки, что бы распознавать и системы проверки. Система распознавания образов – это лингвистическая компетенция.

Логика сказуемых заводит свои правила на запись предложений. Простое предложение надо переписать вот как:

Здесь то, что сказуется стоит под знаком. И через запятую надо обязательно записать «да» или «нет». Мозг работает экономно, и может запомнить «да»или «нет». «Волга впадает в Каспийское море, Да» - «да» писать не надо, запомниться. Категория истинности, как таблица умножения работает у нас. Факт, одно язык, который мы употребляем, другое это этот язык. Значит, нужна система перевода. Когда мы записываем, мы должны все лишнее убрать, что не имеет отношение к экономному кодированию признаков или к экономному кодированию подлежащего, и вообще, что не имеет отношение. К логике предикатов не имеют отношение: может быть, вероятно, разные нормы которое определяют человеческое поведение, должен (в природе ни кто вам не должен!). Через сито перевода проходит только то, что имеет действительное отношение к регистрации факта, признак можно записать со знаком и за этим может стоять реально существующее в природе. Вообще-то простых предложений две формы:

Одна форма говорит, что свойство принадлежит объекту, а вторая, что есть отношения между двумя объектами. Язык предикатов уравнивает подлежащие и дополнение с позиции реальности - две вещи. Начали сказывать с подлежащего одна версия записи появляется, а с дополнения

вторая запись кода. Но в реальности – существуют две вещи и отношения между ними. Логика предикатов, переводя, избавляется от всего лишнего. Логика предикатов интересна тем, что заглядывает внутрь предложения и приписывает ему значения истинности или лжи в зависимости от того в каком отношении находятся подлежащие и сказуемое. А вот логика высказываний проще, ей все равно что там за подлежащие, что там за сказуемое, она не заглядывает внутрь предложения. Ее интересует тот факт, что такое предложение существует и вообще истинно оно или ложно. Логика высказываний очень близка к логике предикатов по своим конструкциям, очень многие формулы одинаковы или похожи.

На слайде: существуют два типа категорических высказываний:

1.Все S есть P. (Все люди млекопитающие)

2.Некоторые S есть P.

Для логики предикатов слова «все» и «некоторые» важны. И в логике предикатов есть специальные знаки для изображения различных конструкций – это так называемые кванторы (за ним ALL стоит) и существует (EXIST).

S(x) и P(x) , кванторы - All , - Exist

SaP : x (S(x)	P(x)). Это запись Все S есть P. Т.е. для каждого х,
который является объектом, он имеет эти свойства.
Если есть один	язык и нам надо перевести на другой, надо

«Нет столь великой вещи, которую не превзошла бы величиной ещё

большая. Нет вещи столь малой, в которую не поместилась бы меньшая» Козьма Прутков

действовать.

Пример изречения приведен на слайде:

Надо начинать перевод со сказуемых, за сказуемым лежит то, что вы сказуете, а сказуете вы то, что у вещи есть такой то признак. Надо искать свойства и отношения. «Великая» это сравнительное свойство – отношение (признак), так есть вещи которые сравниваются. Употребляются сравнительный призанак т.е. надо искать предложение типа «Некоторые S есть P».

Два отношения там названы: «больше» и «меньше». А «большая» и «меньшая» это названы вещи. «Нет столь великой вещи» - назван целый класс, придется использовать кванторы.

Полученная формула: { - v w больше (w,v)} &{ y x

меньше(x,y)}

(для любой v найдется w, для которого справедливо «большая», а для любого y найдется такой х, что будет справедливо «меньшая»).

Следующий пример:

Сидоров и Петров друзья. Они всегда вместе.

Сидоров в институте.

Где Петров?Если правильно записать этот текст на «прологе» (язык такой), запустить интерпретатор, то он ответит, что Петров в институте (для этого необходимо перевести на язык предикатов первого порядка.).

С какого предложения вы начнете перевод? С третьего «Сидоров в институте» - подходит под формулу сказуемое(одна единица, вторая), т.е. в(Сидоров, институт) и дает нам ключ к переводу следующего. Какое было предложение такое и останется, только форма маленько изменяется. Будем считать его базовым, т.е. базовый предикат

находиться_в(персона, место), в(персона, место). Абстрагируемся от Сидорова от института – появилось место, персона. находиться_в(персона, место) – это объект, а в(Сидоров, институт) – экземпляр. Далее думаем, можем мы еще какие экземпляры составить, используя данный предикат. Следующее по простоте перевода является 4 предложение, записать его можно, используя объект.

x в(Петров, x)

Записываем: существует такое место, где находится Петров, но я его не знаю. Далее проще будет записать первое предложение: x {в(Cидоров, x) & в(Петров, x) }. Знак «И» На том основании, что «Сидоров и Петров друзья», если бы у них были другие отношения, тогда бы был другое знак возможно.

Этим примером я хотел, показать что при переводе возникают такие же проблемы, что и при переводе на любой естественный язык (с русского на иностранный). Приходится догадываться, что он там закодировал, а не верить словам. Слова верить нельзя, всегда надо пытаться раскодировать то, что за этим словами скрыто.

Этот перевод упрощает нам решение задачи. Доказано в логике предикатов, что если у вас есть какой-то текст, записанный на этом языке, любой вопрос я могу так пропустить на обработку через весь текст, что извлеку отдута ответ. Чем и пользуются в автоматических программах решениях задач. Программа найдет х, потому что истинна, что Сидоров в институте.

Возникает такой вопрос, что же если любую программу, любой текст записать на языке предикатов первого порядка, а потом толкнуть в любую программу, она мне и ответ даст. Получается, что любую задачу можно решить, если ее текст записать на языке логики предикатов. Но сможете или вы записать текст, удастся или нет записать вам этот текст, зависит от ваших переводческих способностей.

Ваша задача как программиста, это перевести, занести в программу и ждать ответ, который выдаст вам программа. Если ответ вас не устраивает, то надо смотреть исходный код и искать в нем ошибку. Языки, которые занимаются данными задачами – называют, декларативные языки. В разных странах свои любимые языки.

Мы привели примеры и показали, что есть такой подход, есть такая возможность. А если говорить о том, что писать, проверят, читать и слушать надо строже язык определить. А если мы определяем язык строже, значит надо снять все точки «над и». Встает вопрос, как записывать различные экземпляры объектов (предметных единиц)? Предметные константы – имя собственные объектов. Причем 34 яблока и 34 груши это совершенно разные вещи. Переменная – это имена классов (персона, место, вещь). Предикатные константы – это отношения и свойства (для чисел – больше, меньше, равно). Есть алгебра предикатов и исчисление предикатов первого порядка. Алгебра всегда настроена на операциях (знаки и латинские буквы). В языке должны быть логические константы и знаки. Правильные предложения – это отношения, а в скобках названные предметные единицы (константы и переменные). Беру и записываю больше(х,5), я не знаю какой х. Я говорю х=10, надо говорить нет, потому что любое предложение не явно содержит «Да» или «Нет». А если я пишу больше(3,5). Мы не договорились на каком месте большее стоит, но если я сказал «х=10» и «нет», значит я указал на каком месте большее стоит, только неявно.

Когда я пишу просто предложение на языке предикатов первого порядка его принято называть на формальном языке литералом. В программирование литералом называют константу, которая пишется на мете адреса (в ассемблере). Но здесь литералом называют или сам предикат, или его отрицание. Переходим к предложениям. Самое простое предложение есть атом (литерал). Если два атома соединены любым логическим знаком, то это правильное предложение (формула). Если к любой формуле логическим знаком присоединить атом, то это тоже правильное предложение записанное. Таким образом, мы строим более сложные конструкции.

Мы этот язык используем для построения теорий, т.е. для решения каких-то задач. Мы сейчас с вами говорим о числах и об отношениях между числами. Вот я хочу построить теорию отношения между числами. Значит, в первую очередь я должен аксиомы ввести. Первая аксиома: вот если я возьму два числа, то они либо равны, либо больше, либо меньше.

Если два числа в отношении больше, то они не могут быть меньше. Это тоже аксиома.

P1 | P2 | P3 , P1→ P2 , P1→ P3 , P2→ P3 – между числами «или», если Р1 следует не Р2 , если Р1 следует не Р3 , если Р 2 следует не Р3 .

Нельзя меньше, нет смысла больше. Нет больше аксиом, потому что нет смысла больше.

Когда человек решает задачу, у него в голове что-то «крутится», он взял и зарегистрировал это. И теперь я должен проверить соответствует то, что я записал аксиомам. Мы утверждаем если постановку задачи запишем на этом языке, то далее решение задачи на себя возьмет автомат. Будет сложно или легко зависит о того, как мы структурировали задачу. Чем вы лучше структурировали вы код, тем легче вам будет

провести контроль кода и обработку этих кодов. Так вот логика предикатов помогает, т.е нашли формы, которые лучше всего использовать на входе, как для контроля, так и для обработки. Любую задачу, как бы вы ее не записали, надо переписать на язык входа программы, которая будет обрабатывать. Переписать надо используя эти правила:

1.Исключение импликаций

X→ Y ≡ X Y

2.Ограничение отрицаний

X Y ≡ X Y

X Y ≡X Y

3. Разделение переменных

x P(x) & xQ(x) ≡ x P(x) & yQ(y)

4. Исключение кванторов

x y Q(x,y) x Q(x,f(x))

5.Преобразовать в предварённую

x y ... z {Q(x)& P(y)&…& R(z)}

6.Преобразовать в конъюнкт.норм.форму

7.Исключить кванторы x y ... z

8.Исключить символы &

9.Переименовать переменные

Программисту больше нравится квантор «для всех», потому что его программировать лучше, это цикл, обычный цикл.

И «и» не надо писать, потому что это точка между предложениями. Берем нашу задачу, с этими аксиомами, но возьмем другую теорему:

из Р3 влечет не Р1 (Р3 → not Р1). Т.е. это мне придется доказывать. В первую очередь, надо переписать текст задачи, используя эти 9 нормативных преобразований. Переписано здесь для доказательства

методом от противного. Т.е. подготавливаемся к решению задачи.

Таким образом, у нас получилось 6 предложений (так мы «и» не пишем, значит у нас С1, С2, С3, С4, С5 ( это Р3), С6 (это Р1)). Для того, чтобы доказать теорему, я начинаю строить базу тех значений, которые я буду подставлять. Переписываем возможные предикаты. Каждая ветка 1 или 0.

Мы берем набор 111 (Р1Р2Р3) и подставляем и перебираем все наборы (их 8). Многие задачи решаются подстановкой. В таблицу истинности мы тоже подставляем 0 и 1. И вот когда, в последнем столбце 0 или 1, то ваши строки, где 1 (истинные).

У нас система из шести уравнений с шести неизвестными и именно туда мы хотим подставлять. Подставить код и хотим узнать будет в результате 0, условно говоря, или нет.

Подставляем даже варианты, которые не реальны. Нас интересует такой вопрос, а если тут предложения, которые равны нулю. И такое предложение С2. И третье и четвертое дает ноль, но это уже перебор, нам и одного хватает, потому что они все связаны. Таким образом, проведя все подстановки у меня не нашлось не одного случая, такого, что бы ни один из членов в ноль не превратился. Значит мое предположение, что теорема не верна не подтвердилось. А значит, теорема верна.

На проверку мы запустили восемь моделей, вопрос такой, а можно меньше? На семантическом дереве, если посмотреть, что одна какая-то ветка неверна, то и не зачем ее рассматривать.

То есть надо стараться уменьшать деревья, надо проводить проверки. Деревья могут быть бесконечные – и это проблема. Значит, их можно уменьшить их ограничить этим способом. Т.е. уже на конечной части этого

дерева все станет ясно, хотя оно и бесконечное.

Если вы что-то выводите на языке логике предикатов и твердо уверены, что ваша теорема верна, т.е. вы ищете маршрут, то этот маршрут вполне конечный. Эта теорема была доказана логиками где-то в 30-е годы.

Лекция 8

Мы отметили: для того чтобы использовать автоматические вычисления нужно задуматься о сути данных на входе в нормативные

преобразования и использовать подходящие стратегии. Подходящей стратегией является простая подстановка того, что может быть. Но эта подстановка захлебнется, если она столкнется с комбинаторным взрывом (для нашего примера из теории неравенств этого не произошло). У нас появилась аналогия таблицы истинности, по этой аналогии мы оценили общее положение дел. При каждой подстановке в теории у нас отрицательный результат, значит наша теория верна. Отметили проблему размерности семантических деревьев. Существует проблема бесконечных деревьев. К этой проблеме бесконечности деревьев мы и переходим.

Что нужно делать если дерево у нас семантически бесконечное? Мы уже сталкивались с бесконечными деревьями при переборах в глубину, но там у нас были эвристики (эвристика: взять и провести на каком-то уровне границу). Здесь же на каждой трассе лежит подстановка, т.е. вариант подстановки для проверки. Но здесь проблема подстановки, когда она бесконечная. Бесконечное число подстановок мы принципиально не можем проверить все. Но эта проблема в логике предикатов была сразу осознана. Хотя логика предикатов и не такая уж старая (чуть больше 100 лет), но там уже многое сделано. В 30-е годы была доказана теорема: Если вы доказываете от противного и если ваша теорема верна, то в принципе достаточно подставить, даже если дерево бесконечное, конечный набор. Я иду по дереву и делаю подстановки из набора и на каком-то значении у меня превращается в ложь. Т.е. в ложь превратилось на каких-то конечных отрезках. Доказанная теорема говорит о том, что всегда на бесконечности ты наткнешься на то, что рассматривать дальше не надо. И проводим там границу.

Т.о. от бесконечного дерева можно уйти на конечное семантическое дерево, которое содержит трассы из наборов аргументов. При чем каждая трасса вот в таком конечном дереве имеет границу. На каком то предикате она показала, что теорема верна. И вот эти подстановки вы будете делать для множества предложений, в какую-то группу предложений я буду подставлять значение предикатов. Т.о. когда вы подставляете у вас дерево конечное получается.

Те кто занимался автоматическим доказательством теорем вот что придумали: если у меня n предложений, в которые я провожу подстановки. Если их n, нельзя ли добавить какое-то

новое, такое чтобы граница переместилась вверх. Т.е. они хотят из предложений которые я должен

подставить вывести (n+1) предложение, но такое которое позволит дерево уменьшить. Если теорема верна, следовательно, можно добавить все новые и новые выводы, а граница поползет вверх. И в какой то момент

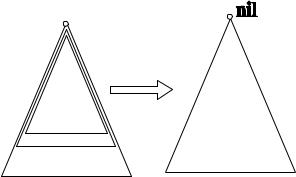
времени эта граница дойдет до верхушке, и не надо нечего подставлять.

Дерево превратилось в nil, в ноль. Вот если вы докажете, что граница может дойти до нуля, то вы автоматически докажите, что ваша теорема верна. Это вторая очень важная теорема в логике предикатов.

У тех кто программировал стала задача генерации новых предложений. Т.е. оказывается доказывая от противного нужно на исходном множестве проводит выводы все новых и новых, до тех пор пока вдруг не получите пустое (nil) предложение по выводу. Как только вы получили предложение пустое по выводу, это значит вы доказали теорему.

Это установки методологические и то что им удалось доказать. А смотрите какое правило применяется для генерации новых. Т.е. у разработчиков автоматизированных программ доказательства стоит задача генерации новых предложений, и они решают ее следующим образом. В исходно множестве предложений они ищут два любых, в одном из которых есть предикат, а в другом его отрицание. Оказывается из них можно вывести третье предложение, в котором эти два предиката пропали, а все остальное что там было связано. Это правило так называемое «резолюции». Его легко понят и даже вашей квалификации хватит, чтобы это понять. Это новое предложение и в исходных его не было. А нужно оно нам для того что бы границы можно было перевести.

Рассмотрим конкретный пример, но сначала скажем о программе, которая будет автоматически доказывать. Программа которая доказываете методом резолюций по работе: ищет пары допускающие

Метод

1.Для множества предложений С ={Ci} найти пару,

допускающую вывод по резолюции, произвести вывод (обозначим результат вывода Ck).

2.Если результат вывода равен nil, то доказательство завершено, иначе включить Ck в множество С и перейти к пункту 1.

вывод, и вот если среди этих пар она найдет nil, то значит теорема доказана, а не найдет надо будет крутится. Пусть компьютер крутится, генерирует все новые и новые. Чисто синтаксически там необходимо искать, чтобы там было P(x1,x2) и не Р. И из них новое, потом новое, новое и до тех пор пока nil не получим. Т.о. программа выливается в эти два пункта по реализации. Тот кто запрограммирует такой алгоритм, создаст программу доказательства теорем в логике предикатов первого порядка. Первая такая программа появились где-то лет 45 назад.

Подводные камни и в этом алгоритме есть. Смотрите, если этих предложений много, и сколько я буду генерировать, какие пары выбирать

– много, но в то же время вся прозрачно, понятно.

Возьмем пример про Сидорова и Петрова. Его мы уже переводили, говорили о нем. Два предложения в условиях и одно в вопросе. Сначала нам надо их привести к нормативному виду, надо избавится от импликаций, квантов, т.д. (по тем восьми пунктам).

Есть в этих предложениях, где есть пара (предикат и его отрицание)? Первое и третье, первое и третье. Значит, мы должны генерировать вывод. Из какой пары генерировать вывод? Выберем первое и третье, из

них выводится в(Сидоров,х).

Теперь беру новое и второе. Из этих двух можно вывести пустое, если я вместо «х» подставлю «институт». Если я дошел до границы значит я теорему доказал. Данная конструкция наглядно показывает схему выводов, которые надо было сделать, чтобы доказать теорему. Теорема: существует место, в котором находится Сидоров. Теперь мы должны привязать это доказательство к условиям задачи, которую мы решаем. Теорему необходимо сопоставить снова с теми предложениями, которые были в условии. Нас интересует не просто место, а какое это место, чему равен х. И те кто программировали эту задачу так ее решили, чтобы людей не путать не показывать им nil, а сразу показать ответ на вопрос. Они переписали сам вопрос в виде всех альтернатив его, которые могут быть. Дописали в(Петров,х). Где было отрицание так записали, где не было с отрицанием. И снова проведем резолюцию и получим, что Петров в институте. Т.е. если добавить альтернативы, то вместо nil получим ответ на вопрос, который стоял в задаче. Оказывается в формальных теориях действительно можно включить в работу автомат, который может и не понимать кто такой Сидоров, что такое институт, но он знает некоторые законы манипуляции формальными выражениями.

Программе сказали, Сидоров и Петров друзья, Сидоров в институте, а она отвечает Петров в институте. Это производит впечатление.

Этот метод является основным, базовым в доказательстве теорем в формальных теориях, где используется логика предикатов первого порядка. Но до сих пор появляются все новые и новые проблемы в