
- •Комплексные числа и действия над ними Практикум
- •Комплексные числа и формы их записи
- •2. Действия над комплексными числами, заданными в алгебраической форме
- •3. Действия над комплексными числами, заданными в тригонометрической или в показательной форме
- •Практикум
- •Решение типового задания
- •Дополнительные задания.
- •Список используемой литературы
- •Оглавление
3. Действия над комплексными числами, заданными в тригонометрической или в показательной форме
Умножение:
При умножении двух
комплексных чисел заданных в
тригонометрической или показательной
формах их модули перемножаются, а
аргументы складываются:
![]() .
.
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
Деление:
При делении двух
комплексных чисел заданных в
тригонометрической или показательной
формах их модули делятся, а аргументы
вычитаются:
![]() ,
,![]() .
.
 (3.4)
(3.4)
![]() (3.5)
(3.5)
Возведение в степень.
Для возведения
комплексного числа в целую положительную
степень
![]() применяют формулу Муавра:
применяют формулу Муавра:
![]() (3.6)
(3.6)
Данная формула является следствием формулы (3.2).
Извлечение корня порядка
 .
.
Для извлечения корня используем формулу:
![]() . (3.7)
. (3.7)
Где
![]() .
.
Точки, соответствующие
![]() являются вершинами правильного
являются вершинами правильного![]() –
угольника, вписанного в окружность с
центром в начале координат и радиусом
–
угольника, вписанного в окружность с
центром в начале координат и радиусом![]()
![]() .
.
Способ построения
для
![]() (рис.2):
(рис.2):
Из начала координат описываем окружность радиуса
 .
.Если
 то из начала координат проводим луч
под углом
то из начала координат проводим луч
под углом
к положительному
направлению
![]() .
Пересечение луча с окружностью дает
точку
.
Пересечение луча с окружностью дает
точку![]() .
.
Вписываем в окружность правильный
 –
угольник, одна из вершин которого
найденная точка
–
угольник, одна из вершин которого
найденная точка .
Точки пересечения
.
Точки пересечения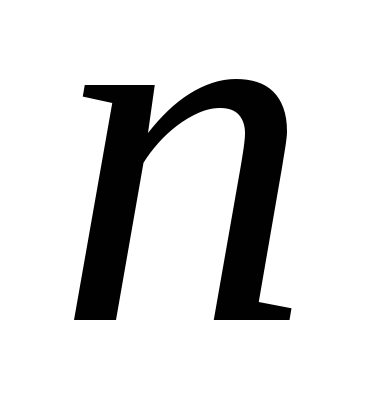 –
угольника и окружности есть решения
–
угольника и окружности есть решения .
.

Рис. 2
Практикум
I. Нарисовать комплексные числа на комплексной плоскости.
1) ![]()
![]()
![]() ;
;
2) ![]()
![]()
![]()
3) ![]()
![]()
![]()
4) ![]()
![]()
![]()
5) ![]()
![]()
![]()
6) ![]()
![]()
![]()
7) ![]()
![]()
![]()
8)
![]()
![]()
![]()
9)
![]()
![]()
![]()
10) ![]()
![]()
![]()
II. Возвести комплексное число в квадрат.
1)
![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ;
;
4)
![]() , 5)
, 5)![]() ,
6)
,
6)![]() ;
;
7)
![]() , 8)
, 8)![]() , 9)
, 9)![]() ;
;
10)
![]() .
.
III. Найти аргумент комплексного числа.
1)
![]()
![]() ,
2)
,
2)![]()
![]() ;
;
3)
![]()
![]() ,
4)
,
4)![]()
![]() ;
;
5)
![]()
![]() 6)
6)![]()
![]() ;
;
7)
![]()
![]() 8)
8)![]()
![]() ;
;
9)
![]()
![]() 10)
10)![]()
![]() .
.
IV.
Выполнить действия:
![]()
![]()
![]()
![]()
1)
![]() ,
,![]() , 2)
, 2)![]() ,
,![]() ,
,
3)
![]() ,
,![]() , 4)
, 4)![]() ,
,![]()
5)
![]() ,
,![]() , 6)
, 6)![]() ,
,![]() ;
;
7)
![]() ,
,![]() , 8)
, 8)![]() ,
,![]() ;
;
9)
![]() ,
,![]() , 10)
, 10)![]() ,
,![]() .
.
V. Перевести комплексное число в показательную форму и возвести в степень. Ответ записать в алгебраической форме.
1)
![]() , 2)
, 2)![]() , 3)
, 3)
![]() ;
;
4)
![]() , 5)
, 5)
![]() , 6)
, 6)![]() ;
;
7)
![]() , 8)
, 8)
![]() , 9)
, 9)![]() ;
;
10)
![]() .
.
VI. Найти модуль комплексного числа.
1)
![]() , 2)
, 2)
![]() ;
;
3)
![]() , 4)
, 4)
![]() ;
;
5)
![]() , 6)
, 6)
![]() ;
;
7) ![]() , 8)
, 8)
![]() ;
;
9)
![]() , 10)
, 10)
![]() .
.
VII. Для данного комплексного числа найти модуль и записать комплексно-сопряжённое число.
1)
![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() ;
;
3)
![]() ,
,![]() ,
,![]() ;
;
4)
![]() ,
,![]() ,
,![]() ;
;
5)
![]() ,
,![]() ,
,![]() ;
;
6)
![]() ,
,![]() ,
,![]() ;
;
7)
![]() ,
,![]() ,
,![]() ;
;
8)
![]() ,
,![]() ,
,![]() ;
;
9)
![]() ,
,![]() ,
,![]() ;
;
10)
![]() ,
,![]() ,
,![]() .
.
VIII.
Вычислить
![]() если
если![]() задано,
изобразить найденные решения на
комплексной плоскости.
задано,
изобразить найденные решения на
комплексной плоскости.
1)
![]() , 2)
, 2)![]() , 3)
, 3)![]() , 4)
, 4)![]() , 5)
, 5)![]() ;
;
6)
![]() , 7)
, 7)![]() ,
8)
,
8)![]() , 9)
, 9)![]() , 10)
, 10)![]() .
.
IX. Решить квадратное уравнение.
1)
![]() , 2)
, 2)
![]() , 3)
, 3)
![]() ;
;
4)
![]() , 5)
, 5)
![]() , 6)
, 6)
![]() ;
;
7)
![]() , 8)
, 8)
![]() , 9)
, 9)
![]() ;
10)
;
10)
![]() .
.
X. Найти частное и остаток от деления.
1)
![]() ,
,
![]() ;
;
2) ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() ;
;
4) ![]() ,
, ![]() ;
;
5) ![]() ,
, ![]() ;
;
6) ![]() ,
, ![]() ;
;
7) ![]() ,
, ![]() ;
;
8) ![]() ,
, ![]() ;
;
9) ![]() ,
, ![]() ;
;
10) ![]() ,
, ![]() .
.
Решение типового задания
Нарисовать комплексные числа на комплексной плоскости, если
![]() ,
,
![]() .
.
Решение:
Для каждого
комплексного числа выпишем действительную
![]() и мнимую
и мнимую![]() части согласно формуле (1.1):
части согласно формуле (1.1):
![]()
![]() ,
,
![]()
![]() .
.
На комплексной
плоскости отметим две точки с
соответствующими координатами:![]()
![]() (рис.3).
(рис.3).

Рис.3
II.
Возвести комплексное число в квадрат,
если:
![]() .
.
Решение:
Воспользуемся
формулой сокращенного умножения
![]() ,
тогда
,
тогда![]()
![]()
применяя формулу
(1.2) к последнему слагаемому, окончательно
получаем ![]()
III.
Найти аргумент комплексного числа,
если:
![]()
![]()
Решение:
Для нахождения
аргумента комплексного числа воспользуемся
формулой (1.6). Определим действительные
![]() и мнимые
и мнимые![]() части заданных комплексных чисел:
части заданных комплексных чисел:![]()
![]()
![]()
![]() .
.
Для числа
![]() ,
следовательно
,
следовательно
![]() .
.
Для числа
![]() ,
следовательно
,
следовательно
![]() .
.
IV.
Выполнить
действия:
![]()
![]()
![]()
![]() ,
если известно, что:
,
если известно, что:
![]()
![]() .
.
Решение:
Рассматривая комплексные числа как двучлены выполним действия сложения, вычитания и умножения:
![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]()
![]() ;
;
Найдем отношение
![]() .
Домножим числитель и знаменатель дроби
на число, сопряжённое к знаменателю
.
Домножим числитель и знаменатель дроби
на число, сопряжённое к знаменателю![]() .
Согласно формуле (1.10) получим:
.
Согласно формуле (1.10) получим:
![]()
![]() .
.
V.
Перевести комплексное число
![]() в показательную форму и возвести в
степень. Ответ записать в алгебраической
форме.
в показательную форму и возвести в
степень. Ответ записать в алгебраической
форме.
Решение:
Для того, перевести
комплексное число в показательную
форму, необходимо найти его модуль
![]() и аргумент
и аргумент![]() .
Для этого воспользуемся формулами (1.5)
и (1.6). определим действительную и
комплексную части числа:
.
Для этого воспользуемся формулами (1.5)
и (1.6). определим действительную и
комплексную части числа:![]() .
Получаем:
.
Получаем:
![]() ;
;
![]() .
.
Тогда в показательной
форме число имеет вид:
![]() .
.
Возведём данное число в четвёртую степень используя формулу (3.6):
![]()
Учитывая, что
функция
![]() имеет период
имеет период![]() ,
окончательно получаем:
,
окончательно получаем:
![]() .
.
Для того, чтобы
перевести число в алгебраическую форму
![]() определим
определим![]() и
и![]() по формулам (1.3):
по формулам (1.3):
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() .
.
VI.
Найти модуль
комплексного числа
![]()
![]()
![]() и записать комплексно сопряжённое
число.
и записать комплексно сопряжённое
число.
Решение:
Число
![]() задано
в алгебраической форме, для нахождения
модуля воспользуемся формулой (1.5):
задано
в алгебраической форме, для нахождения
модуля воспользуемся формулой (1.5):
![]()
![]() следовательно
следовательно
![]() .
.
Число
![]() задано в показательной форме
задано в показательной форме![]() (1.8), откуда следует, что
(1.8), откуда следует, что![]()
Число
![]() задано в тригонометрической форме
задано в тригонометрической форме![]() (1.5) следовательно
(1.5) следовательно![]()
Определим комплексно
сопряжённые числа по формулам (1.9).
Получаем:
![]()
![]()
![]()
VII.
Для данного комплексного числа
![]() найти модуль.
найти модуль.
Решение:
Выражение
![]() представляет из себя произведение двух
комплексных чисел
представляет из себя произведение двух
комплексных чисел![]() и
и![]() возведенных в степень. Для каждого из
них вычислим модуль:
возведенных в степень. Для каждого из
них вычислим модуль:
![]() ,
,
![]() .
.
Согласно формуле
Муавра (3.6), при возведении комплексного
числа в степень, его модуль также
возводится в данную степень, т.е.
![]() ,
,![]() ;
;
При перемножении
двух комплексных чисел. их модули
перемножаются (3.1), (3.2). Следовательно
![]()
VIII.
Вычислить
![]() если
если![]() задано, изобразить найденные решения
на комплексной плоскости.
задано, изобразить найденные решения
на комплексной плоскости.
Решение:
Для вычисления
![]() переведём комплексное число в
тригонометрическую форму, определив
модуль и аргумент.
переведём комплексное число в
тригонометрическую форму, определив
модуль и аргумент.
![]() ,
,
![]() ;
;
![]() ;
;
![]() .
.
В тригонометрической форме получим:
![]()
Для извлечения
корня порядка
![]() воспользуемся формулой (3.7):
воспользуемся формулой (3.7):
где
![]()

![]()
![]() ;
;

![]()
![]() ;
;

![]()
![]() .
.
Построим графическое представление корней:
Вычерчиваем окружность радиуса
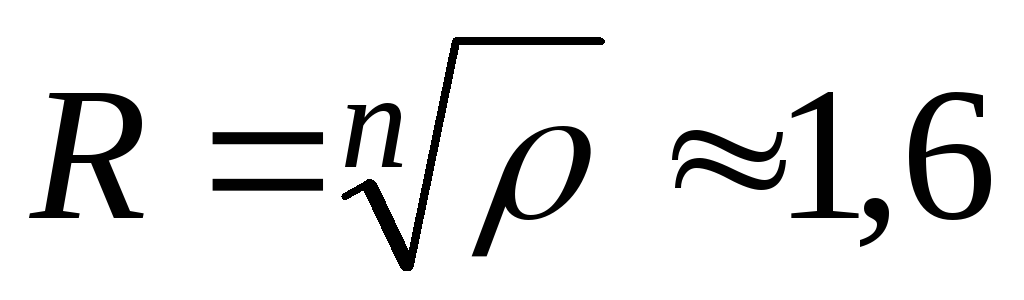
Откладываем угол
 и
на его пересечении с окружностью
отмечаем корень
и
на его пересечении с окружностью
отмечаем корень .
.Вписываем в окружность правильный треугольник (рис. 4).

Рис. 4
IX.
Решить квадратное уравнение
![]() .
.
Решение: Решим данное квадратное уравнение через дискриминант:
![]() ;
;
![]() .
.
Используя формулу
(1.2), получим:
![]() .
Тогда
.
Тогда
![]() .
Или
.
Или
![]()
![]() Что подтверждает теорему о том, что если
многочлен имеет комплексный корень, то
он имеет и комплексно сопряженный
корень.
Что подтверждает теорему о том, что если
многочлен имеет комплексный корень, то
он имеет и комплексно сопряженный
корень.
Х. Найти частное и остаток от деления.
![]() ,
,
![]() .
.
Решение: Для определения частного и остатка воспользуемся формой деления в столбик:
-

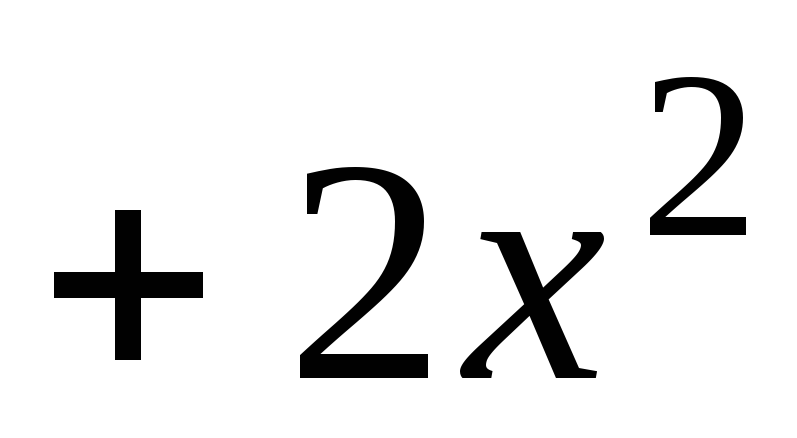




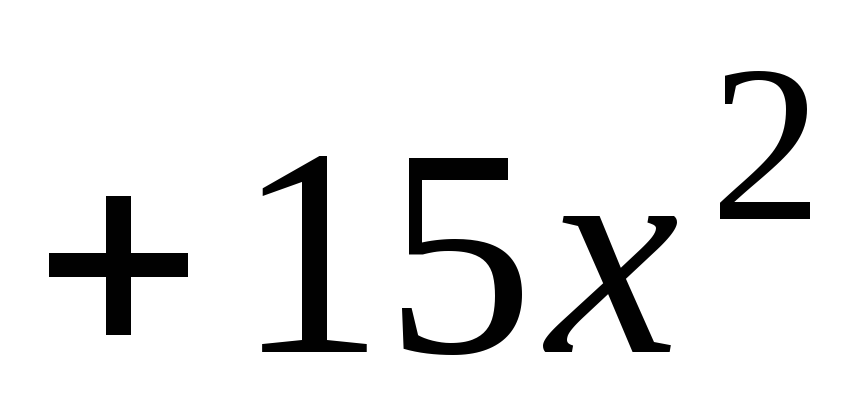

_









При делении получим:
![]() - частное,
- частное,![]() - остаток.
- остаток.
![]() .
.
![]() можно представить
как:
можно представить
как:
![]() Делим в столбик:
Найти частное и остаток от деления.
Делим в столбик:
Найти частное и остаток от деления.
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
При делении
получили:
![]() - частное
- частное
![]()
![]() - остаток
- остаток
![]()
