25.Интегралы от тригонометрических функций. Универсальная тригонометрическая подстановка. Использование тригонометрических формул
Пример 1
Найти
неопределенный интеграл.
Сначала
полное решение, потом комментарии.
Используем
формулу:
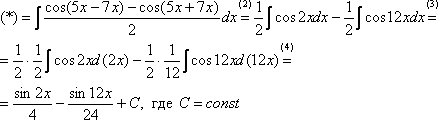
Понижение степени подынтегральной функции
Данный
приём работает, когда подынтегральные
функции нафаршированы синусами и
косинусами в чётных степенях.
Для понижения степени используют
тригонометрические формулы 
, 
и 
,
причем последняя формула чаще используется
в обратном направлении: 
.
Пример 7
Найти
неопределенный интеграл.
Решение:
В
принципе, ничего нового здесь нет, за
исключением того, что мы применили
формулу 
(понизив
степень подынтегральной функции).
Обратите внимание, что я сократил
решение. По мере накопления опыта
интеграл от 
можно
находить устно, это экономит время и
вполне допустимо при чистовом оформлении
заданий. В данном случае целесообразно
не расписывать и правило 
,
сначала устно берем интеграл от 1, затем
– от 
.
Метод замены переменной
Как
уже упоминалось в статье Метод
замены переменной в неопределенном
интеграле,
основной предпосылкой для использования
метода замены является тот факт, что в
подынтегральном выражении есть некоторая
функция 
и
её производная 
:
(функции 
, 
не
обязательно находятся в произведении)
Пример 11
Найти
неопределенный интеграл.
Смотрим
в таблицу производных и замечаем
формулы 
, 
,
то есть, в нашем подынтегральном выражении
есть функция и её производная. Однако
мы видим, что при дифференцировании
косинус и синус взаимно превращаются
друг в друга, и возникает вопрос: как
выполнить замену переменной и что же
обозначать за 
–
синус или косинус?! Вопрос можно решить
методом научного тыка: если мы неправильно
выполним замену, то ничего хорошего не
получится.
Общий
ориентир: в похожих случаях за 
нужно
обозначить функцию, которая находится
в знаменателе.
Прерываем
решение и проводим замену
В
знаменателе у нас всё хорошо, всё зависит
только от 
,
теперь осталось выяснить, во что
превратится 
.
Для
этого находим дифференциал 
:
Или,
если короче: 
Из
полученного равенства по правилу
пропорции выражаем нужное нам выражение:
Итак:
Теперь
всё подынтегральное выражение у нас
зависит только от 
и
можно продолжать решение
Универсальная тригонометрическая подстановка
Универсальная
тригонометрическая подстановка – это
частый случай метода замены переменной.
Её можно попробовать применить, когда
«не знаешь, что делать». Но на самом деле
есть некоторые ориентиры для ее
применения. Типичными интегралами, где
нужно применить универсальную
тригонометрическую подстановку, являются
следующие интегралы: 
, 
, 
, 
и
т.д.
(1)
Производим в исходный интеграл
подстановку: 
, 
, 
.
(2) Приводим знаменатель к общему знаменателю.
(3)
Избавляемся от четырехэтажности дроби,
при этом 
у
нас сокращается. Раскрываем скобки в
знаменателе, двойку в числителе выносим
за знак интеграла.
(4) Приводим подобные слагаемые в знаменателе.
(5)
Интеграл 
решается методом
выделения полного квадрата.
Более подробно с этим методом можно
ознакомиться на уроке Интегрирование
некоторых дробей.
Разложение 
является
подготовкой для осуществления
вышеуказанного приёма
(6) Выделяем полный квадрат и готовим интеграл для интегрирования.
(7)
Интегрируем по табличной формуле 
.
(8)
Проводим обратную замену, вспоминая,
что 
.