
- •25.Интегралы от тригонометрических функций. Универсальная тригонометрическая подстановка. Использование тригонометрических формул
- •Понижение степени подынтегральной функции
- •Метод замены переменной
- •Универсальная тригонометрическая подстановка
- •24.Интегрирование рациональных дробей
- •23.Метод неопределенных коэффициентов
- •22.Интегрирование по частям Интегрирование по частям в неопределенном интеграле
- •Интегрирование заменой переменной
- •Следствия из метода интегрирования заменой переменной
- •Первообразная и неопределенный интеграл, их свойства.
- •Экстремум функции Необходимое условие экстремума
- •Достаточное условие экстремума
- •1) Первое достаточное условие:
- •2) Второе достаточное условие
- •Дифференциал функции
- •Дифференциал функции составляет основную часть ее приращения.
- •Теоремы о дифференцируемых функциях
- •Геометрический и механический смысл производной
- •Геометрический смысл производной
- •Понятие производной Пусть задана некоторая функция . Возьмем какое-нибудь значение из области определения этой функции: . Соответствующее значение функции в этой точке будет равно .
- •Эквивалентные бесконечно малые функции. Таблица эквивалентных б.М. Функций
- •Предельные равенства для эквивалентных б.М. Функций
- •Замечательные пределы
- •Основные неопределенности пределов и их раскрытие.
- •Свойства неопределённого интеграла
- •Примеры исследования последовательностей на монотонность
- •Нестрогая монотонность
- •Основные свойства б.М. И б.Б. Последовательностей
- •Основные понятия и определения
- •Задание последовательности формулой ее общего члена
- •Рекуррентный способ задания последовательности
22.Интегрирование по частям Интегрирование по частям в неопределенном интеграле
Метод вычисления интегралов, называемый интегрированием по частям, основан на правиле дифференцирования произведения.
Пусть ![]() —
функции, дифференцируемые на некотором
промежутке
—
функции, дифференцируемые на некотором
промежутке ![]() .
Тогда, как известно, дифференциал
произведения этих функций вычисляется
по формуле
.
Тогда, как известно, дифференциал
произведения этих функций вычисляется
по формуле
![]()
Взяв неопределенный интеграл от обеих частей этого равенства, получим:
![]() Так
как
Так
как ![]() ,
а
,
а ![]() ,
,
то
получаем: ![]() ,
откуда
,
откуда ![]() .
.
Поскольку ![]() уже
содержит произвольную постоянную, в
правой части полученного равенства
уже
содержит произвольную постоянную, в
правой части полученного равенства ![]() можно
опустить и записать равенство в виде
можно
опустить и записать равенство в виде
![]()
|
(1) |
Полученная формула называется формулой интегрирования по частям.
При
выводе формулы (1) мы предположили, что
функции ![]() и
и ![]() дифференцируемы.
Этой формулой обычно пользуются в тех
случаях, когда подынтегральное
выражение
дифференцируемы.
Этой формулой обычно пользуются в тех
случаях, когда подынтегральное
выражение ![]() проще,
чем подынтегральное выражение
проще,
чем подынтегральное выражение ![]() .
.
Заметим,
что одно и то же подынтегральное выражение
можно различными способами записать в
виде ![]() .
Например,
.
Например,
и
т. д. Поэтому иногда приходится испытывать
различные формы такой записи, прежде
чем метод приведет к успеху. Обычно
стараются подынтегральное выражение
разбить на части ![]() и
и ![]() так,
чтобы вид
так,
чтобы вид ![]() был
не сложнее, чем вид
был
не сложнее, чем вид ![]() ,
а вид
,
а вид ![]() проще,
чем вид
проще,
чем вид ![]() .
В частности, полезно иметь в виду, что
для таких функций, как
.
В частности, полезно иметь в виду, что
для таких функций, как ![]()
![]()
![]()
![]() ,
производные имеют вид более простой,
чем сами функции. Поэтому в большинстве
случаев эти функции удобно принимать
за функцию
,
производные имеют вид более простой,
чем сами функции. Поэтому в большинстве
случаев эти функции удобно принимать
за функцию![]() .
.
Пример
1. Вычислим
по частям неопределенный интеграл ![]() .
.
Решение. Положим ![]() .
Тогда
.
Тогда ![]() .
.
Используя формулу интегрирования по частям (1), получаем:
![]()
Замечание. При
нахождении ![]() не
пишут промежуточную произвольную
постоянную
не
пишут промежуточную произвольную
постоянную ![]() ,
так как она не оказывает влияния на
окончательный результат.
,
так как она не оказывает влияния на
окончательный результат.
Интегрирование заменой переменной
Суть данного метода заключается в том, что в рассмотрение вводится новая переменная интегрирования или, что тоже самое, делается подстановка. После этого заданный в условии интеграл сводится либо к табличному интегралу, либо к нему сводящемуся.
Если
в неопределенном
интеграле ![]() сделать
подстановку
сделать
подстановку ![]() ,
где функция
,
где функция ![]() -
функция с непрерывной первой производной,
то тогда
-
функция с непрерывной первой производной,
то тогда ![]() и
согласно свойству
6 неопределенного интеграла имеем,
что:
и
согласно свойству
6 неопределенного интеграла имеем,
что:
![]()
Эта формула называется формулой замены переменной в неопределенном интеграле.
Задание. Найти
интеграл ![]()
Решение. Сделаем
замену переменной: ![]() ,
далее приведем интеграл
к табличному виду и
решим его. В конце решения делаем обратную
замену.
,
далее приведем интеграл
к табличному виду и
решим его. В конце решения делаем обратную
замену.
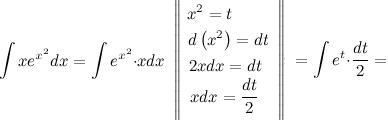
![]()
Ответ. ![]()
Следствия из метода интегрирования заменой переменной
Используя метод подстановки, можно получить следующие соотношения для некоторых интегралов, которые рационально использовать уже в конечном виде, а не каждый раз производить вычисления:
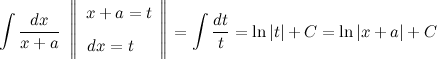
то есть
![]()
Аналогично можно показать, что
![]()
![]()
![]()
Подобные соотношения можно было вывести и с использованием метода внесения под дифференциал.
Первообразная и неопределенный интеграл, их свойства.
Определение первообразной.
Первообразной
функции f(x) на
промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство ![]() для
любого х из
заданного промежутка.
для
любого х из
заданного промежутка.
Если
принять во внимание тот факт, что
производная от константы С равна
нулю, то справедливо равенство ![]() .
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
.
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение неопределенного интеграла.
Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается ![]() .
.
Выражение ![]() называют подынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
называют подынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называетсянеопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
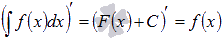 Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции. Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы. ,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.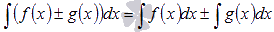 Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для
доказательства третьего и четвертого
свойств достаточно найти производные
от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
