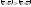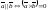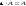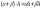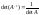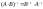- •5. Обратная матрица. Достаточное условие существования обратной матрицы.
- •Основные действия над матрицами
- •Операционное исчисление
- •Производные и дифференциалы высших порядков
- •14. Векторное произведение векторов и его свойства.
- •15. Смешанное произведение векторов и его свойства.
- •24. Гипербола. Определение. Вывод канонического уравнения.
- •25. Парабола. Определение. Вывод канонического уравнения.
Векторы Вектор - это направленный прямолинейный отрезок, т.е. отрезок, имеющий длину и определенное направление. Свойства линейных операций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;![]() ;
;
Сложение
векторов. Пусть ![]() и
и![]() –
два произвольных вектора. Возьмем
произвольную точкуО и
построим вектор
–
два произвольных вектора. Возьмем
произвольную точкуО и
построим вектор ![]() ;
затем от точкиА отложим
вектор
;
затем от точкиА отложим
вектор ![]() .
Вектор
.
Вектор![]() ,
соединяющий начало первого слагаемого
вектора с концом второго,
называетсясуммой этих
векторов и обозначается
,
соединяющий начало первого слагаемого
вектора с концом второго,
называетсясуммой этих
векторов и обозначается ![]() (рис.
1).
(рис.
1).
![]()
Рис. 1
Ту
же сумму можно получить иным способом.
Отложим от точки О векторы ![]() и
и![]() .
Построим на этих векторах как на сторонах
параллелограммОАСВ.
Вектор
.
Построим на этих векторах как на сторонах
параллелограммОАСВ.
Вектор ![]() –
диагональ параллелограмма – является
суммой векторов
–
диагональ параллелограмма – является
суммой векторов![]() и
и![]() (рис.
2).
(рис.
2).
![]()
Рис. 2
Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).
Рис. 3
Вычитание
векторов. Разностью ![]() векторов
векторов![]() и
и![]() называется
такой вектор
называется
такой вектор![]() ,
который в сумме с вектором
,
который в сумме с вектором![]() дает
вектор
дает
вектор![]() :
:![]()
![]() .
.
Если
векторы ![]() и
и![]() привести
к общему началу, то разность представляет
собой отрезок, соединяющий их концы и
направленный от «вычитаемого» к
«уменьшаемому» (рис. 4).
привести
к общему началу, то разность представляет
собой отрезок, соединяющий их концы и
направленный от «вычитаемого» к
«уменьшаемому» (рис. 4).
![]()
Таким
образом, если на векторах ![]() и
и![]() ,
отложенных из общей точкиО,
построить параллелограмм ОАСВ,
то вектор
,
отложенных из общей точкиО,
построить параллелограмм ОАСВ,
то вектор ![]() ,
совпадающий с одной диагональю, равен
сумме
,
совпадающий с одной диагональю, равен
сумме![]() ,
а вектор
,
а вектор![]() ,
совпадающий с другой диагональю, –
разности
,
совпадающий с другой диагональю, –
разности![]() (рис.
5).
(рис.
5).
![]()
Умножение
вектора на число. Произведением вектора ![]() на
действительное число
на
действительное число![]() называется
вектор
называется
вектор![]() (обозначают
(обозначают![]() ),
определяемый следующими условиями:
),
определяемый следующими условиями:
1) ![]() ,
,
2) ![]() при
при![]() и
и![]() при
при![]() .
.
Очевидно,
что при ![]()
![]() .
.
Построим,
например, векторы ![]() и
и![]() для
заданного вектора
для
заданного вектора![]() (рис.
6).
(рис.
6).
![]()
Рис. 6
Из
определения следует: два
вектора ![]() и
и![]() коллинеарны
тогда и только тогда, когда имеет место
равенство
коллинеарны
тогда и только тогда, когда имеет место
равенство![]() :
:
Два
ненулевых вектора называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Нулевой вектор
считается коллинеарным любому другому
вектору.
Для коллинеарности вектора ![]() ненулевому
вектору
ненулевому
вектору ![]() необходимо
и достаточно, чтобы существовало такое
число λ, что
необходимо
и достаточно, чтобы существовало такое
число λ, что![]()
векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.
Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны
Для
компланарности трех векторов ![]() и
и ![]() трехмерного
пространства необходимо и достаточно,
чтобы их смешанное произведение
равнялось нулю.
трехмерного
пространства необходимо и достаточно,
чтобы их смешанное произведение
равнялось нулю.
Условия ортогональности векторов. Два вектора
a
и
b
ортогональны (перпендикулярны), если их скалярное произведение равно нулю
a Угол
между векторами
![]()
![]()
Векторным
произведением
вектора
 на вектор
на вектор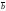 называется
вектор
называется
вектор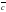 ,
который:
,
который:
Перпендикулярен векторам
 и
и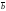 .
.Имеет длину, численно равную площади параллелограмма, образованного на векторах
 и
и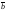 .
.
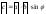 ,
где
,
где
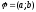
Векторы
 ,
,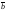 и
и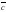 образуют правую тройку векторов.Свойства:
образуют правую тройку векторов.Свойства:
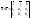
ДИФФиринциал
Производная
функции f(x)
есть некоторая функция f
’(x),
произведенная из данной функции.Функция
y=f(x),
имеющая производную в каждой точке
интервала (a;b)
называется дифференцируемой
в этом
интервале. Для нахождения производной
сложной функции надо производную данной
функции по промежуточному аргументу
умножить на производную промежуточного
аргумента по независимому аргументу.
![]() .
.
Рассмотрим функцию, заданную параметрически: x = φ(t), y = ψ(t). Покажем, что для нахождения производной y'x, совсем необязательно находить выражение явной зависимости yот x.
Теорема
12. Пусть
функция x
= φ(t) имеет
обратную функцию t
= Ф(x). Если
функцииx=φ(t), y
= ψ(t) дифференцируемы
и φ'(t) ≠ 0,
тогда![]() :
: ![]()
![]()
Диффиринциал Производной функции γ=f(x) называется функция f'(x), равная пределу отношения приращения функции f(x) к приращению аргумента, когда последнее произвольным образом стремится к нулю:
![]()
где ?х - приращение аргумента х.
Производная
функция у обозначается также через у'
и ![]()
Если функция γ=f(x) изображается кривой в декартовых координатах, то γ' при рассматриваемом значении аргумента выражает угловой коэффициент касательной к кривой в соответствующей точке, т. е. γ'=tg α, где α - угол наклона касательной к оси X. Производная имеет не только геометрическое толкование, она выражает скорость изменения функции относительно аргумента, например скорость движения, интенсивность нагрузки, силу тока, теплоемкость и т. п.
Если
функция имеет в рассматриваемой точке
производную, то она в этой точке
непрерывна; таким образом, непрерывность
является необходимым
условием
существования производной, но это
условие не является достаточным, так
как непрерывность не гарантирует
существования производной.
Дифференциалом функции f(x)
в точке х называется главня линейная
часть приращения функции.
Обозначается dy или df(x).Из
определения следует,
что dy = f(x)x илиdy = f(x)dx.Можно
также записать: ![]()
Замечательные
пределы 1) ![]() ;(Первый
замечательный предел)
;(Первый
замечательный предел)
2) ![]() (Второй
замечательный предел)Данный предел
относят обычно к неопределенностям
вида 1∞.
Раскрытие подобных неопределенностей
как правило, связано с использованием
второго замечательного предела.
(Второй
замечательный предел)Данный предел
относят обычно к неопределенностям
вида 1∞.
Раскрытие подобных неопределенностей
как правило, связано с использованием
второго замечательного предела.
Интегрирование тригонометрических выражений
Универсальная тригонометрическая подстановка
Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными sin x и cos x, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать R(sin x;cos x), где R - знак рациональной функции.
Вычисление
неопределенных интегралов типа![]() сводится
к вычислению интегралов от paциoнaльнoй
фyнкции подстановкой
сводится
к вычислению интегралов от paциoнaльнoй
фyнкции подстановкой![]() ,
которая называется универсальной.Действительно,
,
которая называется универсальной.Действительно,
![]() ,
,
![]() Поэтому
Поэтому
![]()
где R1(t) - рациональная функция от t.
Исследование поведения функций и их графики
При решении этой задачи находят:
1) область определения функции;
2) точки разрыва и исследуют поведение функции в граничных точках области определения;
3) находят нули функции и промежутки ее знакопостоянства;
4) находят асимптоты;
5) критические точки и интервалы монотонности;
6) точки перегиба и интервалы выпуклости.
Замечание. Если функция f(x) четная, т.е. f(x) = f(–x), или нечетная, т.е. f(x) = – f(–x), то исследование функции достаточно провести для x³0, а затем по свойству четности или нечетности построить график при x<0.
Завершают исследование функции построением ее графика.
Матрицы
Матрицей называется прямоугольная
таблица чисел, сод ержащаяm
строк одинаковой длины.Матрицы равны
между собой, если равны все их
соответствующие элементы.
ержащаяm
строк одинаковой длины.Матрицы равны
между собой, если равны все их
соответствующие элементы.
Матрица, у которой число строк и столбцов равно – называется квадратной.
Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной.
Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е.
Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной.
Матрица, у которой все элементы равны нулю, называется нулевой.
Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.

где
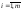

5. Обратная матрица. Достаточное условие существования обратной матрицы.
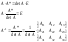
Для того чтобы матрица имела обратную достаточно того, чтобы она была невырождена.
Основные действия над матрицами
Сумма (разность) матриц.
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера.
Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij bij
Обозначение: С = А + В = В + А.
Умножение матрицы на число.
Операция умножения матрицы любого размера на произвольное число сводится к умножению каждого элемента матрицы на это число.

Свойства: (АВ) =А В
А() = А А
Пример: Даны матрицы А = Произведение двух матриц.
Замечание: Операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй. В противном случае произведение матриц не определено.
Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:Обозначение: AB = C;
Из приведенного определения видно, что каждый элемент матрицы С равен алгебраической сумме произведений элементов i – той строки матрицы А на соответствующие элементы j – го столбца матрицы В.Свойства:
1) Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Транспонирование матриц
Определение. Матрицу АТ называют транспонированной матрицей А, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы АТ.(т.е. строки матрицы А заменены на столбцы и наоборот)
А
=
 ; АТ=
; АТ= ;
;
методы интегрирования неопределенных интегралов
Замена переменной
Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.
Если функция f(z) непрерывна на [, ], функция z =g (x) имеет на [a,b] непрерывную производную и α ≤ g(x) ≤ β, то
∫ f(g(x)) g' (x) dx = ∫f(z) dz, (8.3)
причем после интегрирования в правой части следует сделать подстановку z=g(x).
Для доказательства достаточно записать исходный интеграл в виде:
∫ f(g(x)) g (x) dx = ∫ f(g(x)) dg(x).
Например:
1) ![]() ;
;
2)![]() .
.
Метод интегрирования по частям
Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные производные. Тогда, по правилу дифференцирования произведения,
d(uv)= udv + vdu или udv = d(uv) -vdu.
Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:
∫ udv = uv - ∫ vdu. (8.4)Эта формула выражает правило интегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx.
Пусть, например, требуется найти x cosx dx. Положим u = x, dv = cos x dx, так что du=dx, v=sinx. Тогда
∫ x cos x dx = ∫ x d(sin x) = x sin x - ∫ sin x dx = x sin x + cos x + C.Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,∫ xk lnmx dx, ∫xk sin bx dx, ∫ xk cos bx dx, ∫xk e ax dxи другие, которые вычисляются именно с помощью интегрирования по частям.
Подведение
под знак дифференциала.Метод подведения
под знак дифференциала основан на
приведении подынтегрального выражения
к виду ![]() .
Далее применяется метод подстановки:
вводится новая переменная
.
Далее применяется метод подстановки:
вводится новая переменная ![]() и
после нахождения первообразной для
новой переменной, возвращаемся к
исходной переменной, то есть
и
после нахождения первообразной для
новой переменной, возвращаемся к
исходной переменной, то есть
![]()
Определение
1. Функция
вида![]() ,
где
,
где![]() и
и![]() -
многочлены, называется дробно-рациональной
функцией. Мы будем рассматривать, как
правило, правильные дроби, то есть
дроби
-
многочлены, называется дробно-рациональной
функцией. Мы будем рассматривать, как
правило, правильные дроби, то есть
дроби![]() ,
где степень многочлена в числителе
меньше степени многочлена, стоящего в
знаменателе.
,
где степень многочлена в числителе
меньше степени многочлена, стоящего в
знаменателе.
Начнем с дробей, в которых в знаменателе стоит квадратный трехчлен.
Обычно дробно-рациональные функции интегрируются с помощью разложения на простейшие дроби.
![]() .
.
Здесь подынтегральная функция следующим образом раскладывается на простейшие дроби:
![]()
![]() =
=![]() .
.
Получаем систему:
![]()
Решая
ее, получаем ![]() значит
значит![]() =
=![]() .
.
Для
интегрирования иррациональной функции,
содержащей ![]() используется
подстановка
используется
подстановка![]() . Чтобы
проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степенейx,
применяется подстановка в форме
. Чтобы
проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степенейx,
применяется подстановка в форме ![]() ,
гдеn полагается
равным наименьшему общему кратному
знаменателей всех дробных степеней,
входящих в данную функцию.
Рациональная
функция x под
знаком корня n-ой
степени, т.е. выражение вида
,
гдеn полагается
равным наименьшему общему кратному
знаменателей всех дробных степеней,
входящих в данную функцию.
Рациональная
функция x под
знаком корня n-ой
степени, т.е. выражение вида ![]() ,
интегрируется с помощью
подстановки
,
интегрируется с помощью
подстановки![]() .
Интегрирование
иррациональных функций, содержащих
.
Интегрирование
иррациональных функций, содержащих![]() и
и![]() ,
рассматривается на странице
,
рассматривается на странице
непрерывность функцииПусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0).
Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:
|
|
f(x) = f(x0), |
Пусть
переменная x
стремится к a,
оставаясь больше a,
и при этом ![]() .
Тогда числоA
называют правосторонним
пределом (или пределом
справа)
функции
.
Тогда числоA
называют правосторонним
пределом (или пределом
справа)
функции ![]() и обозначают любым из символических
выражений
и обозначают любым из символических
выражений
![]()
Понятие
левостороннего предела (или предела
слева) вводится аналогичным образом.
В этом случае ![]() приx → a
со стороны меньших значений:
приx → a
со стороны меньших значений:
![]()
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
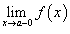 и
правосторонний предел
и
правосторонний предел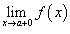 ;
;Эти односторонние пределы конечны.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
Неопределённый
интеграл
![]()
где F - первообразная функции f (на промежутке); C - произвольная постоянная.
Основные свойства
1. ![]()
![]()
2. ![]()
![]()
3.
Если ![]() то
то
![]()
4. ![]()
Определители1. При транспонировании (замене строк определителя на соответствующие столбцы) определитель не изменится.
2. Разложение определителя по любой строке или любому столбцу: определитель равен сумме произведения элементов любого ряда на их алгебраические дополнения.3. При перестановке двух строк или столбцов абсолютная величина определителя не изменится, а знак определителя меняется на обратный.4. Общий множитель строки или столбца можно вынести за знак определителя.5. Свойство линейного преобразования в определителе . Определитель не изменится, если к какой- либо строке (столбцу) прибавить другую строку (столбец) предварительно
умноженную на какое- либо число.6. Если элементы одной строки равны элементам другой строки определителя, то определитель равен нулю .
Определителем называется число, записанное в виде квадратной таблицы:
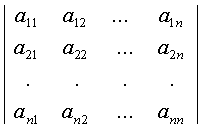 .
.
Таблица
ограничивается слева и справа
вертикальными линиями, ![]() -называется
элементами определителя (
-называется
элементами определителя ( ![]() -номер
строки,
-номер
строки, ![]() -номер
столбца).
-номер
столбца).
Главная
диагональ определителя содержит
элементы ![]() ,
противоположная диагональ называется
побочной.
,
противоположная диагональ называется
побочной.
Порядком определителя называется число строк (столбцов) квадратной таблицы.
Определитель II порядка
вычисляется по формуле:![]()
Определитель III порядка можно вычислить по правилу Сарруса:
оПРЕДЕЛЁННЫЙо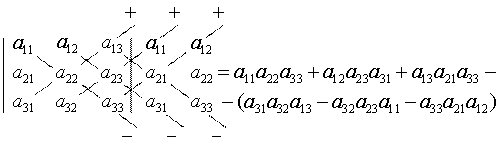
Определённый интеграл
I.
Величина определенного интеграла не
зависит от обозначения переменной
интегрирования, т.е. ![]() ,
где х, t – любые буквы.
,
где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
![]()
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
![]()
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
![]()
V. Постоянный множитель можно выносить за знак определенного интеграла.
![]()
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
![]()
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
![]()
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
Определенный интеграл был введен для ограниченных на отрезке функций. Естественно распространить это понятие на случай бесконечных промежутков и бесконечно больших функций.
Пусть f (x) определена
при x ≥ a и
интегрируема на отрезке [a; ξ],
где ξ ≥ a.
Если существует конечный предел  то
говорят, что функцияf интегрируема
в несобственном смысле на промежутке [a; +∞),
а несобственный
интеграл
то
говорят, что функцияf интегрируема
в несобственном смысле на промежутке [a; +∞),
а несобственный
интеграл![]() сходится:
сходится:
|
|
Если ![]() не
имеет конечного предела при ξ → +∞,
то говорят, что несобственный интеграл
расходится.
не
имеет конечного предела при ξ → +∞,
то говорят, что несобственный интеграл
расходится.
Аналогично
определяется несобственный интеграл ![]()