Фильтры_лекция

Лекция №2. Классы и типы цифровых фильтров

Содержание лекции:

-два класса цифровых фильтров, их математическое описание, общая характеристика типов цифровых фильтров.

Цель лекции:

-ознакомиться с математическим описанием рекурсивных цифровых фильтров и нерекурсивных с линейной фазочастотной характеристикой, изучить типы цифровых фильтров с предоставлением их краткой характеристики.

К одному из основных направлений цифровой обработки сигналов (ЦОС) относится цифровая фильтрация. Цифровая фильтрация – это процесс преобразования цифровых сигналов с целью выделения и/или подавления определенных частот этих сигналов, а устройство, выполняющее фильтрацию, называется фильтром. На рисунке 2 представлены классы и типы цифровых фильтров (ЦФ).

Цифровые фильтры

Рекурсивные (БИХ)

Нерекурсивные (КИХ) с линейной ФЧХ

НЧ

Баттерворта

Тип 1

Тип 2

Тип 3

Тип 4

ВЧ

Чебышева 1 и 2

ПФ

Золотарева-Кауэра

РФ

НЧ

НЧ

ПФ

ВЧ

ВЧ

ПФ

Преобразователь

ПФ

ПФ

Гильберта,

Дифференциатор,

РФ

Дифференциатор

Преобразователь

АК

Гильберта

Рисунок 2

Из рисунка 2 видно, что в области цифровой фильтрации разработчик систем ЦОС имеет дело с реализацией двух классов фильтров:

-фильтры с бесконечной импульсной характеристикой (БИХ-фильтры), то есть с импульсной характеристикой, имеющей бесконечную длину во временной области; такой фильтр называют еще рекурсивным из-за наличия обратной связи;

-фильтры с конечной импульсной характеристикой (КИХ-фильтр), то

есть с импульсной характеристикой, ограниченной по времени ( с какого-то момента времени она становится равной нулю); из-за отсутствия обратной связи такие фильтры называют нерекурсивными.

Оба класса фильтров относятся к классу линейных систем с постоянными параметрами, в которых входная x(n) и выходная y(n) последовательности

связаны отношениями типа свертки. Если обозначить через	h(k) отклик
системы на единичный импульс, то получим свертку вида:
n
y(n) h(k ) x(n k ),	(2.1)
k 0
где x(n), y(n) - отсчеты входного и выходного сигналов;
h(k) – импульсная характеристика;

x(n - k) - входной отсчет, задержанный на k интервалов дискретизации.

Цифровые фильтры полностью описываются во временной области разностными уравнениями, а в z-области – передаточными функциями.

В БИХ-фильтре отсчет выходного сигнала определяется значениями входного и выходного сигналов, а в КИХ-фильтре – только значениями входного сигнала.

Рекурсивные фильтры представляют собой системы с обратной связью и описываются разностными уравнениями вида

N 1	M 1
y(n) bi x(n i) ak y(n k),		(2.2)
i 0	k 1

где bi и ak – вещественные коэффициенты, причем хотя бы один ak ≠ 0; x(n-i) - входные отсчеты, задержанные на i периодов дискретизации T ; y(n-k)-выходные отсчеты, задержанные на k периодов дискретизации T; N и M – постоянные целые числа, причем М ≥ N.

Передаточная функция рекурсивного фильтра в соответствии с (2.2) имеет вид

N 1

bi z i

H (z) i 0 , (2.3)

M 1

1 ak z k

k 0

где z– комплексная переменная, причем z re j ˆ .

При r 1 после подстановки z в (2.3) получаем комплексную частотную

характеристику

N 1

bi e j ˆ i

H (e j ˆ ) i 0 , (2.4)

M 1

1 ai e j ˆ k k 0

модуль которой представляет собой ненормированную амплитудно-частотную характеристику (АЧХ)

A( ˆ ) H (e j ) ,

(2.5)

ˆ

а аргумент – фазочастотную характеристику (ФЧХ)

( ˆ ) arg H (e jwˆ )

(2.6)

Нерекурсивные фильтры представляют собой системы без обратной связи; их разностные уравнения и передаточные функции получаются из (2.2) и (2.3) при ak = 0 соответственно

N 1

y(n) bi x(n i) , (2.7)

i 0

N 1

H (z) bi z i , (2.8)

i 0

где N - число коэффициентов; N-1 – порядок фильтра.

Амплитудно-частотные и фазочастотные характеристики вычисляются из (2.8) при z e j ˆ согласно (2.5) и (2.6) [ 1 ].

	Необходимо отметить,	что коэффициенты a	k	передаточной функции
рекурсивного фильтра по		абсолютной величине		равны коэффициентам

разностного уравнения, но противоположны по знаку, а коэффициенты bi разностного уравнения и передаточной функции нерекурсивного фильтра полностью совпадают и представляют собой отсчеты его импульсной характеристики.

Таким образом, для построения систем цифровой фильтрации требуется эффективная реализация соотношения типа дискретной свертки (2.1), которая раскладывается на операции умножения и накапливающего суммирования, а также операции задержки, что учитывается в архитектуре сигнальных процессоров при реализации процессов цифровой фильтрации.

На рисунке 2 также представлена возможная реализация фильтров низкой частоты (НЧ), высокой частоты (ВЧ), полосовых фильтров (ПФ), режекторных фильтров (РФ), а также амплитудных корректоров (АК), преобразователей Гильберта и дифференциаторов. Из рисунка 2 видно, что БИХ-фильтры

различают по свойствам частотных характеристик на фильтры Баттерворта, Чебышева 1 и 2 и Золотарева-Кауэра.

Дадим краткую характеристику вышеприведенным типам фильтров.

Отличительной особенностью фильтров Баттерворта является то, что они обладают максимально плоской амплитудно-частотной характеристикой (АЧХ) в полосе пропускания и монотонной в полосе задерживания, причем в полосе пропускания ФЧХ близка к линейной. Данные фильтры являются фильтрами общего назначения, так как они наиболее полно соответствуют условиям безыскаженной передачи сигналов, поэтому применяются при необходимости сохранения соотношений составляющих сигнала по амплитуде и фазе.

Фильтры Чебышева характеризуются крутым спадом АЧХ (при том же порядке), однако это приводит к увеличению нелинейности фазовой характеристики в полосе пропускания. Амплитудно-частотные характеристики фильтров Чебышева 1 рода в полосе пропускания имеют равноволновой характер, а в полосе задерживания монотонно убывают. Фильтры Чебышева II рода (инверсные) обладают монотонной АЧХ в полосе пропускания и равноволновой в полосе задерживания.

Фильтры Чебышева I широко применяются в радиосистемах для подавления помех от соседних радиостанций. Инверсные фильтры применяются значительно реже, чем фильтры I рода, поскольку они требуют реализации нулей. Это не только усложняет программную и аппаратную реализации, но и увеличивает собственный шум фильтра за счет введения умножений в числителе передаточной функции. Тем не менее инверсные фильтры обладают и важным положительным свойством: их АЧХ является монотонной в полосе пропускания.

Фильтры Золотарева-Кауэра (эллиптические) характеризуются равноволновой АЧХ как в полосе пропускания, так и в полосе задерживания. Данный тип фильтров применяют в задачах, требующих высокой избирательности и не критичных к виду фазовой характеристики.

Амплитудные корректоры – это фильтры, предназначенные для выравнивания АЧХ системы в пределах ее рабочей полосы до установленных норм. Амплитудные корректоры подключаются каскадно с корректируемым частотным трактом и устанавливаются либо перед трактом, либо после него.

Преобразователь Гильберта осуществляет демодуляцию однополосного сигнала, который получается выделением одной из боковых полос амплитудномодулированного сигнала. Результатом демодуляции является низкочастотный сигнал, представляющий собой огибающую узкополостного сигнала. Данное преобразование применяется в системах радиосвязи для задач модуляции и демодуляции узкополосных сигналов и сдвига частоты.

Дифференциатор выполняет операцию дифференцирования в заданной области частот. Обычно цифровые дифференциаторы применяются в системах

управления, где требуется линейная зависимость сигнала управления от частоты исходного сигнала, генерируемого управляющим объектом.

Лекция №3. Рекурсивные цепи первого и второго порядков

Содержание лекции: временной и частотный анализ, оценка на устойчивость рекурсивных цепей первого и второго порядков.

Цель лекции: изучить структуру рекурсивных цепей первого и второго порядков, временные и частотные характеристики, уметь оценивать цепи на их устойчивость.

Большую роль в линейных дискретных системах с постоянными параметрами играют рекурсивные цепи 1-го и 2-го порядков, на их основе можно построить цепи более высоких порядков.

Передаточная функция (ПФ) рекурсивной цепи 1-го порядка имеет вид:

H (z)	b	b z 1
	0	1	,	(3.1)
	1 a z 1
		1

Если числитель передаточной функции H(z) равен 1, то цепь для удобства будем называть базовым звеном 1-го порядка. Важной характеристикой для описания свойств линейных дискретных систем является импульсная характеристика (ИХ), как ее реакция на единичный импульс. ИХ звена 1-го порядка имеет вид

	b0 ,			n 0
h(n) =	b ( a )n b ( a )n 1				, n 0	(3.2)
	0	1	1	1

На рисунке 3 представлена прямая структурная схема цепи 1-го порядка

x(n)

b0

y(n)

+

1

1

b1

a1

Рисунок 3

Нуль z0

и полюс z* передаточной функции вычисляются по формулам

z 0

b1

, z *

a1 .

(3.3)

b0

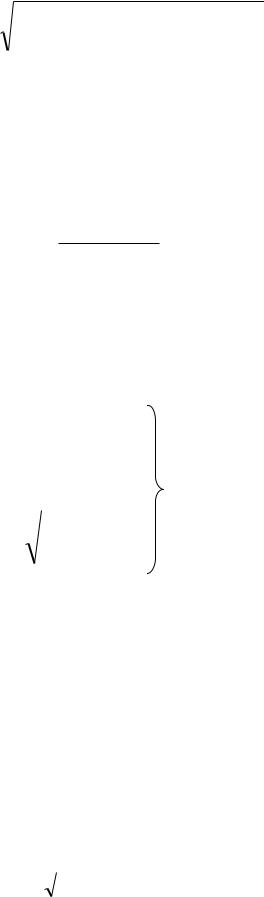
Условием устойчивости является | z* | = | a1 | < 1. Из формулы (3.I) при z=ej T получаются выражения для амплитудно-частотной характеристики (АЧХ)

(b0

ˆ

2

ˆ

2

A( ˆ )

H (e j T )

b1 cos )

(b1 sin )

,

ˆ

2

ˆ

2

(1 a1 cos )

(a1 sin )

и фазочастотной характеристики (ФЧХ)

( ˆ ) arctg

a1 sin ˆ

arctg

b1 sin ˆ

.

1 a cos ˆ

1 b cos ˆ

1

1

ˆ

где ˆ 2 f - нормированная круговая частота.

Нормированной АЧХ называют соотношение

A( )

A( )

.

max[ A( )]

Из формулы 3.6 следует, что 0

A( ) 1.

(3.4)

(3.5)

(3.6)

Для оценки вида АЧХ удобно пользоваться формулами экспресс-

анализа, которые позволяют определить значения АЧХ на трех частотах

0, и / 2

A(0)		b0 b1
			1 a1
A( )			b0 b1
		1		a1						(3.7)
A( / 2)						b 2			b	2
						0		1
				1			a 2
								1

Рекурсивная цепь 2-ого порядка описывается передаточной функцией

	H (z)	b b z 1		b z 2
		0 1			2		(3.9)
		1 a z 1	a		2	z 2
		1

Нули и полюсы H(z) определяются из решений уравнений

b0 z 2 b1 z b2 0

и z 2 a1 z a2 0

(3.10)

Из этих уравнений находятся: 1. Нули

	b		b2	4b b
Z1,02	1	1		0 2		.	(3.12)
		2b0

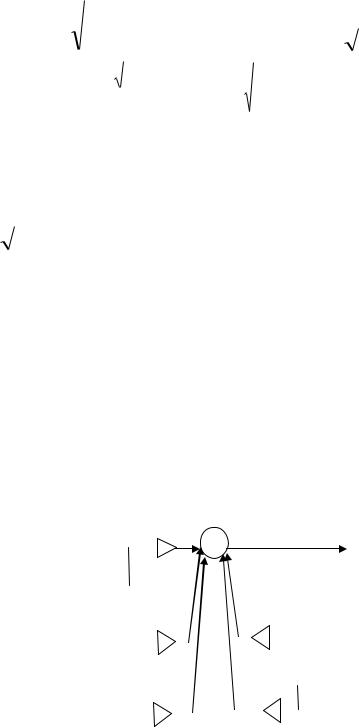
Если дискриминант неотрицательный, то имеем вещественные нули, в противном случае, H(z) обладает двумя комплексно-сопряженными нулями

z10,2

r0 e j 0 ,

(3.13)

b2

b1

где

r0

,

0

arccos

.

b0

2 b0b2

2. Полюсы	z*		a1 a12 4a2				a1			a12	a		(3.14)
												2
	1,2	2			2					2

Если дискриминант неотрицательный, то имеем вещественные полюсы, в противном случае, H(z) обладает двумя комплексно-сопряженными полюсами

z1*,2 r*e j *,

(3.15)

*

*

arccos

a1

где

r a ,

.

2

2r*

Импульсная характеристика цепи второго порядка при комплексно-

сопряженных полюсах имеет вид

h(n) b r*n

sin[(n 1) * ]

b r*(n 1)

sin(n * )

b r*(n 2)

sin[(n 1) * ]

(3.16)

0

sin( * )

1

sin( * )

2

sin(

* )

Как

следует из

выражения

(3.16)

слагаемое,

у которого степень r

меньше нуля, равно нулю, поскольку рассматриваются только физически возможные цепи (у таких цепей реакция не может опережать воздействие).

Прямая структурная схема цепи второго порядка представлена на рисунке

3

X(n)

b0

Y(n)

+

1

b1

- a1

1

1

1

b2

- a2

Рисунок 3

Важным свойством цепи является ее устойчивость. Для устойчивости цифровой цепи второго порядка необходимо, чтобы все полюса передаточной функции находились внутри единичного круга z-плоскости, то есть | Z* | < 1.

Данное условие накладывает определенные ограничения на величину коэффициентов знаменателя передаточной функции рекурсивного фильтра. Для рекурсивного фильтра второго порядка с комплексно-сопряженными полюсами эти ограничения соответствуют

a1	< 2 a2 < 2 и 0 < a2 < 1			(3.17)

Цепи второго порядка в зависимости от соотношения коэффициентов могут обладать различной избирательностью: низкочастотной (НЧ), высокочастотной (ВЧ), полосовой (П), режекторной (Р).

Из передаточной функции (3.9) при z e jw получаются выражения для АЧХ и ФЧХ

(b0

ˆ

ˆ

2

ˆ

ˆ

2

b1 cos b2 cos2 )

(b1 sin b2 sin 2 )

A( )

(1 a cos ˆ a

2

cos2 ˆ )2

(a sin ˆ a

2

sin 2 ˆ )2 ;

(3.18)

1

1

ˆ

ˆ

ˆ

ˆ

a1 sin a2

sin 2

b1 sin b2 sin 2

( ) arctg

arctg

∙(3.19)

1 a cos ˆ

a

2

cos 2 ˆ

b

b cos ˆ

b

cos 2 ˆ

1

0

1

2

Для определения избирательности цепи необходимо уметь строить АЧХ по характерным точкам, к которым обычно относят значения АЧХ на следующих частотах:

					0		*	.
0,		2 , ,				и

Последние две частоты соответствуют фазам нуля 0 и полюса * , при

этом максимум АЧХ находится приблизительно на частоте * .

Для оценки вида АЧХ удобно пользоваться формулами экспресс-анализа для вычисления АЧХ и ФЧХ на трех частотах:

1. 0; z 1;

b0

b1

b2

A(0)

;

(0)

0.

1 a a

2

1

z j;

2. / 2;

A( / 2)

(b

b )2

b2

0

2

1

;

(1 a2 )2

a12

(3.20)

( / 2) arctg

a1

arctg

b1

.

1 a

b

b

1

0

2

1;

3. ; z

A( ) b0 b1 b2 ; ( ) 0. 1 a1 a2

Для оценки минимума и максимума АЧХ необходимо произвести

		0	ˆ 0		0		*	ˆ *		*	.
вычисления A( ) при			2 f			и		2 f