4. Приемы устных вычислений умножения и деления трехзначных и многозначных чисел

Приемы устных вычислений с трехзначными и многозначны­ми числами касаются действий умножения и деления с числами, оканчивающимися нулями.

Прием вычислений для случаев вида 200 • 3; 800 : 4; 800 : 200

В этом случае целые сотни (или тысячи в примерах вида 4 000 • 3) рассматриваются как разрядные единицы, что позволяет свести эти случаи к табличному умножению и делению:

200х3 800:4 800:400

2 сот. х3 = 6 сот. 8 сот.: 4 = 2 сот. 8 сот.: 4 сот. = 2

200 • 3 = 600 800 : 4 - 200 800 : 400 = 2

Прием вычисления для случаев вида

70 • 6; 320: 8; 4 800:800

В этом случае целые десятки (или сотни) также рассматриваются как разрядные единицы, что позволяет свести эти случаи либо к таб­личному умножению и делению, либо применять к ним приемы уст­ного внетабличного умножения и деления в пределах 100.

Например:

70-6 320 : 8 4 800 : 800

7 дес. • 6 = 42 дес. 32 дес.: 8 = 4 дес. 48 сот.: 8 сот. = 6 70 • 6 - 420 320 : 8 - 40 4 800 : 800 - 6

При хорошем владении разрядным и десятичным составом чисел дети без труда осваивают эти приемы самостоятельно. Для подведения ребенка к осознанию смысла этих приемов можно ис­пользовать примеры — помощники:

Например:

Вычисли: 4х7 40х70 140:2

40х7 14:2 140:20

Прием вычисления для случаев вида

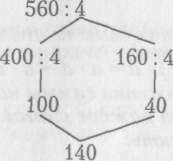
840:2; 560 : 4; 303 Х2; 180х4

8 подобных случаях необходимо использовать как знание де­сятичного состава чисел, так и приемы устного внетабличного ум­ножения и деления в пределах 100.

Например:

Приемы умножения и деления на разрядную единицу

(умножения и деления на 10, 100, 1 000)

Умножение на разрядную единицу переводит число в следую­щие разряды. Технически такое умножение добавляет нули спра­ва в запись числа, что увеличивает количество содержащихся в нем разрядов на количество добавленных нулей.

Например:

65-10 = 650 43-100 = 4300 75 • 1 000 - 75 000

Делить на 10, 100, 1 000 в области натуральных чисел можно только числа, содержащие соответствующее количество младших разрядов, не имеющих значащих цифр. Технически при этом как бы убирают соответствующее количество нулей справа, начиная с последнего.

Например:

650:10 = 65 8600:100 = 86 71 000 :1 000 = 71

4500:Ш = 450 123000 : Щ= 1 230

Во всех остальных случаях деления на разрядную единицу в об­ласти натуральных чисел будет получаться деление с остатком.

Например:

642 :10 - 64 (ост. 2) 5 140 : 100 = 51 (ост. 40)

Письменное умножение и деление

1. Умножение в столбик.

2. Деление в столбик.

1. Умножение в столбик

Используемые математические законы и правила

Вычисления произведения многозначного числа на однозначное или многозначного числа на многозначное требует применения письменных приемов вычислений (письменного алгоритма ). Этот алгоритм построен на основе законов сложения и умножения на­туральных чисел.

Правило умножения суммы на число:

(а + Ь+с)-а-а-а + Ь-Л + с-Л

При умножении суммы на число можно умножить на это число каждое слагаемое и полученные резуль­таты сложить.

В качестве суммы рассматривается трехзначное (многозначное) число, представляемое в виде суммы разрядных слагаемых. Ум­ножение таким образом представленного многозначного числа на однозначное выполняется в соответствии с правилом умножения суммы на число.

Например:

125х3 = (100+ 20+ 5) -3 = 100х3 + 20 х3 + 5х3 = 300 + 60+ 15 = 375

Переводя данный способ умножения в запись «столбиком», получа­ем письменный прием (алгоритм) умножения на однозначное число.

Правило умножения числа на сумму:

ах (Ъ + с + р) = ахЬ + ахс + ахр

При умножении числа на сумму можно умножить это число на каждое слагаемое и полученные резуль­таты сложить.

Это правило является основой приема умножения многозначного числа на многозначное. Первый множитель — это число, умножаемое на сумму. В качестве суммы в этом случае рассматривается второй множитель, представляемый в виде разрядной суммы. Умножение многозначного числа на многозначное выполняется в соответствии с правилом умножения числа на сумму.

Например:

123 • 212 = 123 • (200 + 10 + 2) - 123 • 200 + 123 • 10 + 123 • 2 -= 24 600 + 1 230 + 246 - 26 076

Переводя данный способ умножения в запись «столбиком», получа­ем письменный прием (алгоритм) умножения на многозначное число.

Приемы вычислений

Письменное умножение на однозначное число

Записать умножение столбиком можно подробно. Например:

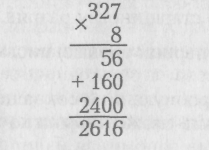
Но обычно используется краткая запись, поскольку главным достоинством письменных приемов умножения является краткость записи вычислений:

Сложность состоит в том, что достоинства этого приема на пер­вых порах составляют главную проблему его усвоения, поскольку все опущенные в короткой записи промежуточные вычисления необхо­димо выполнять в уме (устно), запоминая при этом промежуточные результаты (сколько и каких единиц нужно прибавить к следующе­му разряду).

Учебник математики для 3 класса содержит подробное описа­ние процесса умножения «в столбик», пошагово оговаривающее каждое умственное действие по выполнению умножения и сложе­ния получаемых отдельных сумм:

1. Умножаю единицы: 7 • 8 = 56, 56 это 5 дес. и 6 ед.

2. 6 ед. пишу под единицами, а 5 дес. запоминаю и прибавляю их к десяткам после умножения десятков.

3. Умножаю десятки: 2 дес. • 8 = 16 дес. К 16 дес. прибавляю 5 дес., которые были получены при умножении единиц:

16 дес. + 5 дес. = 21 дес. — это 2 сот. и 1 дес. Пишу 1 дес. под десятками, а 2 сот. запоминаю и прибавляю их к сотням после ум­ножения сотен.

4. Умножаю сотни: 3 сот. • 8 = 24 сот. К 24 сот. прибавляю 2 сот., которые были получены при умножении десятков.

24 сот. + 2 сот. = 26 сот. — это 2 тыс. и 6 сот. Пишу 6 сот. под сотнями, 2 тыс. под тысячами. Читаю ответ: 2616.

Для прочного усвоения письменных приемов умножения ребе­нок должен:

1. Запомнить правильную запись: разряд записывается под со­ответствующим разрядом.

2. Запомнить правильный порядок выполнения действия: ум­ножение начинаем с младших разрядов (справа налево).

3. Овладеть технологией запоминания и добавления излишних разрядных единиц, получаемых при умножении однозначных чисел, в следующий по старшинству разряд.

Для облегчения (на первых уроках) письменного приема умно­жения можно:

1) производить подробную, а не сокращенную запись приема. В этом случае выполнять сложение можно по записям неполных произведений, а не в уме, запоминая излишние разрядные едини­цы (использование этого приема рекомендуется для детей, плохо считающих в уме);

2) производить запись промежуточных вычислений рядом с примером или на черновике — в этом случае все необходимые для запоминания и добавочного прибавления разрядные единицы будут зафиксированы, и ребенок не будет их «терять».

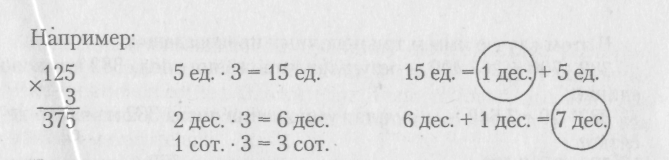
Такая запись часто кажется человеку, владеющему алгоритмом письменного умножения, излишней, слишком подробной. Даже учителя редко пользуются указанными приемами помощи ребен­ку. Однако следует обратить внимание на то, что взрослый чело­век (особенно тот, кто учился в «докалькуляторную эпоху») имеет очень большую практику употребления этого алгоритма и, естест­венно, он уже, как говорят педагоги, автоматизировался, т. е. взрос­лый человек часто не задумывается над процессом его примене­ния. Ребенку, который только начинает этому учиться намного труднее, особенно, если он при этом не очень тверд в таблице ум­ножения и сложении двузначных чисел в уме.

Письменное умножение на двузначное (и многозначное) число

опирается на правило умножения числа на сумму. Прием письмен­ного умножения на двузначное число можно записать подробно:

329 • 24 = 329 • (20 + 4) - 329 • 20 + 329 • 4 - 6580 + 1316 - 7896 или кратко (в столбик):

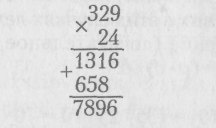
Число 1316 называют первым неполным произведением, число 6580 называют вторым неполным произведением. Последний нуль (в разряде единиц) в записи числа 6580 при вычислениях в стол­бик опускают, лишь подразумевая его, для скорости записи. При этом цифру 8 (количество десятков) записывают в разряде десят­ков (таким образом, второе неполное произведение записывается со сдвигом влево на одну позицию).

Аналогично производится вычисление и запись умножения на трехзначное число:

В этом случае имеем три неполных произведения:

382 • 700 = 267 400 — результат умножения числа 382 на число единиц;

382 • 20 =7 640 — результат умножения числа 382 на число де­сятков;

382 -9 = 3 438 — результат умножения числа 382 на число сотен.

Результат умножения 382 • 729 дает сумма этих неполных про­изведений.

Записи последних нулей в неполных произведениях при вычис­лениях в столбик опускаются для экономичности записи, однако они подразумеваются, что показано сдвигом влево на один разряд каждого следующего неполного произведения.

Технически, несмотря на экономичный способ записи, выпол­нение умножения многозначного числа на двузначное или трех­значное число — процесс сложный и трудоемкий, требующий не только знания способов записи и порядка выполнения действий при письменных вычислениях, но и прочного знания таблицы ум­ножения (до автоматизма), а также умения производить сложение двузначных и однозначных чисел в уме.

Особые случаи

В качестве особых случаев рассматривают случаи умножения целых чисел (чисел с нулями) вида: 35 • 20; 532 • 300; 2540 • 400.

В основе умножения в этих случаях лежит правило умножения числа на произведение (сочетательное свойство умножения): а • (Ъ • с) = (а • Ь) • с = (а • с) • Ь.

Например:

35 • 20 - 35 • (2 • 10) - (35 • 2) • 10 - 70 • 10 - 700

2540-400 = 2540-(4-100) = (2540-4)-100= 10160-100 = 1016000

Письменное умножение чисел с нулями рассматривается от­дельно в связи с тем, что при записи таких вычислений в столбик происходит нарушение общего правила записи чисел при письмен­ном умножении.

Записывают такие случаи следующим образом:

При этом уже не соблюдается установка: «записываем разряд под соответствующим разрядом». Записывают одну под другой значащие цифры множителей. Например, в последнем случае значащая цифра 4'(число сотен) второго множителя записывается под значащей цифрой 4 (число десятков) первого множителя. Далее умножение производится по принципу «многозначное число ум­ножаем на однозначное», а результат помножается в уме на количе­ство десятков и сотен в множителях. Технически это выглядит как дописывание к результату справа такого же количества нулей, как в обоих множителях.

Сложные случаи письменного умножения

К сложным случаям письменного умножения относят все случаи вычислений, в которых происходит либо нарушение способа запи­си (для краткости вычислений), либо нарушение порядка выпол­нения алгоритма.

В общем случае при записи умножения в столбик следует запи­сывать разряд под соответствующим разрядом, а вычисления начинать с умножения первого множителя на единицы младшего разряда (разряда единиц), далее умножают первый множитель на число десятков второго множителя, далее — на число сотен и т. д. Таким образом находят неполные произведения, которые затем складывают, получая результат умножения.

В сложных случаях может происходить нарушение формы записи.

В первых трех случаях нарушение формы записи можно объяс­нить наличием нулей (незначащих цифр) в множителях, что по­зволяет на первом вычислительном этапе мысленно опускать их, помножая затем результат на нужное количество десятков.

В четвертом случае происходит нарушение порядка выполнения действий — после умножения первого множителя на число единиц второго множителя, сразу переходим к умножению первого множи­теля на число сотен, поскольку число десятков второго множителя обозначено цифрой 0. Подразумевается, что умножение первого мно­жителя на 0 десятков дает нулевой результат во втором неполном произведении. Поэтому для экономичности записи его опускают, под­разумевая его «по умолчанию». В связи с этим при умножении первого множителя на число сотен второе (фактически — третье) неполное произведение записывают со сдвигом влево на два разряда, посколь­ку первая справа значащая цифра этого неполного произведения бу­дет цифрой сотен, поэтому ее следует записать в разряд сотен.

Для того чтобы ребенок понял смысл всех этих многочисленных действий «по умолчанию», при знакомстве с этими трудными случаями следует сначала производить полные записи и выполнять все, пред­писанные алгоритмом действия, а не просто указывать ребенку, что куда следует «сдвигать». Затем, сравнивая два вида записи (полный и сокращенный) нужно помочь ребенку понять, какие элементы и этапы полного алгоритма и полной записи можно опустить, и что при этом произойдет с формой записи. В этом случае ребенок будет вы­полнять трансформации формы записи и порядка выполнения дей­ствий при письменном умножении осознанно, что способствует по­ниманию вычислительного приема и формированию осознанной вычислительной деятельности школьника.