2. Деление в столбик

Вычисления результатов деления многозначного числа на од­нозначное или многозначного числа на многозначное требует при­менения письменных приемов вычислений (письменного алгорит­ма деления). Этот алгоритм построен на основе правил деления суммы на число, деления числа на произведение и приемов нахож­дения результатов деления с остатком.

Используемые математические законы и правила

Правило деления суммы на число:

(а + Ь + с) : Л = а : д. + Ь : Л + с : Л

При делении суммы на число можно разделить на это число каждое слагаемое и полученные результа­ты сложить.

В качестве суммы рассматривается трехзначное (многозначное) число, представляемое в виде суммы разрядных или удобных сла­гаемых. Деление таким образом представленного многозначного числа на однозначное выполняется в соответствии с правилом де­ления суммы на число. Например:

396:3 = (300 + 90 + 6):3 = 300:3 + 90:3 + 6:3 = 100 + 30 + 2 = 132 365 :5 = (350 + 15) : 5 = 350 : 5 + 15 : 5 = 70 + 3 - 73 Переводя данный способ деления в запись «столбиком», полу­чаем письменный прием (алгоритм) деления на однозначное число. Правило деления числа на произведение:

а : (Ь • с) = (а : Ь) : с

При делении числа на произведение можно разде­лить это число сначала на один множитель, а затем полученный результат разделить на второй множи­тель.

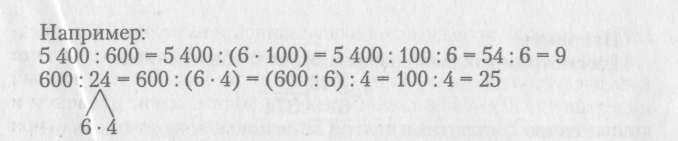
Использование данного правила позволяет устно выполнять де­ление, которое в общем случае требует письменных вычислений.

Деление с остатком является основным видом действий, после­довательно выполняемым при письменном делении.

Свойства и способы деления с остатком см. с. 169—172.

Приемы вычислений

Письменное деление на однозначное число

Прием письменного деления включает такие операции: замену делимого суммой удобных слагаемых (это чаще называют выделе­нием неполных делимых), деление на делитель каждого слагаемого (неполного делимого) и сложение полученных частных. Для по­лучения цифр частного используют прием подбора. Не всегда по­лучается сразу подобрать оптимальную цифру частного. Каждую подобранную цифру частного проверяют, умножая ее на делитель находят разницу между неполным делимым и полученным произ­ведением. Если этот остаток меньше делимого, то цифра частного выбрана верно, ее можно записывать в частное и продолжать про­цесс со вторым неполным делимым и т. п.

Письменное деление может быть с остатком и без остатка.

Письменное деление всегда начинают с высших раз­рядов, в отличие от письменного умножения.

В традиционном учебнике математики использован поэтапный подход к формированию письменного алгоритма деления:

1-й этап: рассматриваются случаи вида 794 : 2; 984 : 4 — первое неполное делимое однозначное;

2-й этап: рассматриваются случаи вида 376 : 4; 198 : 6 — первое неполное делимое двузначное;

3-й этап: рассматриваются случаи с нулями в частном (на конце или в середине);

4-й этап: рассматривается деление чисел, оканчивающихся нулями.

Учебник математики для 3 класса содержит подробное описа­ние процесса деления «в столбик», пошагово оговаривающее каж­дое умственное действие по выполнению подбора и проверки цифр частного, нахождения количества разделенных разрядных единиц, нахождения остатка.

Например:

Рассмотрим как выполнено деление с объяснением:

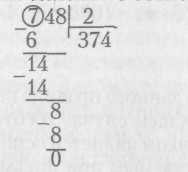
1. Делю сотни: 7 сот. делю на 2, можно взять по 3 сот. В частном будет 3 сот.

Проверяю, сколько сотен разделилось: 3 сот. -2 = 6 сот. Нахожу остаток от деления сотен: 7 сот. - 6 сот. = 1 сот.

2. Делю десятки: 1 сот. = 10 дес. и еще 4 дес. — это 14 дес. 14 дес. делю на 2 — можно взять по 7. Записываю в частном 7 в разряде десятков. 7 дес. • 2 = 14 дес. Нахожу остаток: 14 дес. - 14 дес. = 0. Десятки разделились все.

3. Делю единицы — единиц 8. 8 делю на 2, можно взять по 4. Проверяю: 4-2 = 8. Пишу в частном 4 в разряде единиц. Единицы разделились все: 8-8 = 0. Остатка нет. Деление закончено.

Ответ: 374.

При делении вида 45) 6 : 8 ход рассуждений аналогичен, только первое неполное делимое — 45 десятков, поскольку 4 сотни нельзя разделить на 8 так, чтобы получить в частном сотни. Таким образом, первая значащая цифра частного в этом случае будет цифрой десятков.

При делении многозначных чисел для самопроверки полезно заранее определить, сколько цифр должно получиться в записи час­тного. Выделение первого неполного делимого и определение его десятичного состава как раз и является приемом, позволяющим оп­ределить количество цифр частного.

Например:

В случае деления 748 : 2 первое неполное делимое — 7 сотен, поскольку 7 сотен можно разделить на 2 так, чтобы в частном полу­чились сотни. Следовательно, первой значащей цифрой частного будет цифра сотен, тогда в частном будет три цифры (сотни, де­сятки и единицы).

Во втором случае деления 456 : 8 первое неполное делимое — 45 десятков, следовательно первой значащей цифрой частного бу­дет цифра десятков, тогда в частном будет две цифры (десятки и единицы).

Обучение ребенка этому приему самопроверки является важ­ным способом формирования осознаваемой вычислительной дея­тельности. Особенно важен этот прием при выполнении деления, приводящего к случаям получения нулей в частном.

Первое неполное делимое 56 сотен (поскольку 5 тысяч нельзя разделить на 8 так, чтобы получить в частном тысячи), значит, первой цифрой частного будет цифра сотен. Следовательно, в част­ном будет три цифры (сотни, десятки и единицы). Данное рассуж­дение полезно отметить постановкой соответствующего количества точек в частном. Это предупредит распространенную в таких слу­чаях ошибку — потерю цифры частного.

Далее деление выполняется по общему алгоритму:

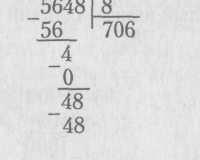
При объяснении получения нуля в частном следует в речевом сопровождении компенсировать условность сокращенной записи деления в столбик: 4 десятка нельзя разделить на 8 так, чтобы в частном получились целые десятки, поэтому в разряде десятков частного ставим 0. 4 десятка — это 40 единиц, да еще 8 единиц — делим 48 на 8...

При делении чисел, оканчивающихся нулями, следует посто­янно применять прием «прикидки» цифр частного, это поможет ребенку не терять нули в конце деления.

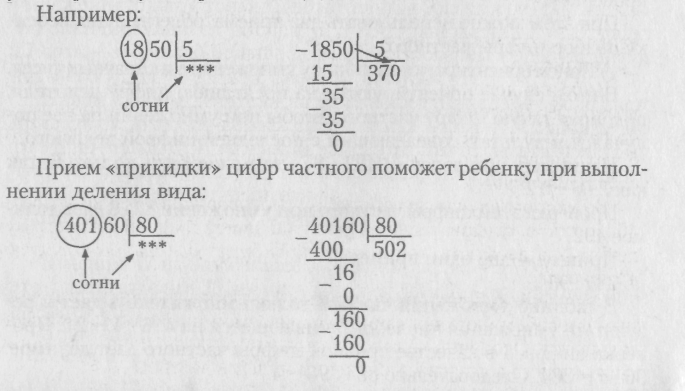
Деление на двузначное и трехзначное число

В основе устного деления на двузначное и трехзначное число лежит свойство деления числа на произведение:

а : (Ь • с) = (а : Ъ) : с

При делении числа на произведение можно разделить это число сначала на один множитель, а затем полу­ченный результат разделить на второй множитель.

Например:

240: 30 = 240 : (3 • 10) = (240 :10) : 3 - 24 : 3 - 8 2700 :900 = 2700 : (9 • 100) = 2700 : 100 : 9 = 27 : 9 = 3 Однако в основе письменного деления на разрядные числа ле­жит не данный устный прием, а общий алгоритм деления на одно­значное число. Например:

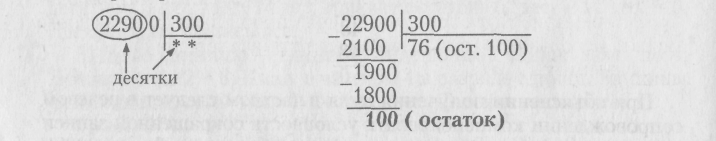
При ознакомлении с делением на двузначное число сначала рас­сматривают случаи, когда в частном получается одна цифра.

Эту цифру частного находят приемом подбора с последующей проверкой.

При этом можно использовать два приема, облегчающих ребен­ку подбор цифры частного:

1) Прием ориентировки на таблицу умножения однозначных чисел.

В этом случае ориентируются на последнюю цифру делителя, подбирая такую цифру частного, чтобы при умножении на нее по­лучался результат, совпадающий с последней цифрой делимого.

Например, при делении 492 : 82 это может быть только 6, так как 2 • 6 = 12.

Проверка этой цифры частного при умножении 82 • 6 дает дели­мое 492.

Приведем еще один пример:

384 :96

В таблице умножения числа 6 только множитель 4 дает в ре­зультате умножения число, оканчивающееся на 4: 6 • 4 = 24. Про­верка цифры 4 в качестве пробной цифры частного дает делимое: 96 • 4 = 384. Следовательно 384 : 96 = 4.

Этот прием помогает быстро найти цифры частного, если речь идет о делении без остатка.

2) Прием замены делителя ближайшим разрядным числом.

В этом случае делитель заменяется на ближайшее разрядное чис­ло (в данном случае вместо 96 можно брать 90). В отношении раз­рядного числа легче найти пробную цифру частного. В данном случае деление 38 дес. на 9 дес. дает пробную цифру частного — 4. Затем ее проверяют, умножая на нее делитель. Цифра может по­дойти, а может и не подойти, поскольку ближайшее разрядное чис­ло берут не по правилу округления, а по принципу отбрасывания единиц. В этом случае проводится коррекция и уточненная цифра частного записывается в ответ.

Процесс деления многозначных чисел на двузначное и трех­значное технически очень сложный и трудоемкий. В старших клас­сах на уроках физики и химии, где бывают нужны многозначные вычисления детям рекомендуют пользоваться калькуляторами.

Эти же приемы облегчения поиска пробной цифры частного можно использовать при делении на трехзначное число.

Например:

738:246

Заменим число 246 ближайшим разрядным числом — это 200. 200 это 2 сот. Разделим 7 сот. на 2 сот. В частном можно пробовать цифру 3. Проверим эту пробную цифру: умножим 246 на 3, получим 738. Значит 738 : 246 - 3

Например:

В частном будет одна цифра, поскольку 145 дес. нельзя разде­лить на 364 так, чтобы в частном получились десятки. В таблице умножения числа 4 только множители 4 и 9 дают в результате чис­ла, оканчивающиеся числом 6. 3 сот., умноженные на 9, дадут 27 сот. — это число больше делимого. Проверим пробную цифру частного 4: 364 -4 = 1 456. Значит 1 456 :364 = 4.

Прием замены делителя на ближайшее разрядное число часто приводит к тому, что первая подобранная таким путем цифра час­тного не подходит и ее нужно изменять. Это происходит потому, что замена происходит не по правилам округления, а простым от­брасыванием единиц делителя. .

Например:

Заменим 47 на ближайшее разрядное число — это 40, т. е. 40 — это 4 дес. Разделим 28 дес. на 4 дес., получим 7 — это пробная циф­ра частного.

Проверяем, подходит ли цифра 7 : 47 • 7 = 329 — это больше, чем 282, значит, в частном должно быть меньше, чем 7.

Проверяем, подходит ли цифра 6: 47 • 6 = 282. Значит, 282:47 = 6.

Использование первого из обозначенных приемов в сочетании с приемом замены делителя на ближайшее разрядное число позволит уменьшить затраты сил и времени на поиски пробных цифр частного.

Использование общего приема округления делителя также позволит быстрее и точнее искать пробную цифру частного. В част­ности, в данном случае по правилам округления следовало ок­руглять 47 до 50, а значит первая пробная цифра частного — это 6 : 50 • 6 = 300 > 282, но округление произведено с увеличением, а результат близок к делимому, значит можно пробовать 6 в каче­стве цифры частного.

Наиболее трудоемки случаи, требующие нескольких прикидок по цифрам частного. Особо рассматривается случай, когда при пер­вой пробе получается число 10.

Например:

В частном одна цифра. Прием округления, как и прием замены делителя на ближайшее разрядное число, дает в качестве делителя число 100. Первая пробная цифра частного в этом случае получает­ся 10. Но число 10 содержит две цифры, поэтому оно не подходит.

Пробуем в качестве цифры частного 9. Проверяем: 127 • 9 = 1143 > > 1016, значит, цифра 9 не подходит.

Пробуем 8: 127 • 8 = 1016. Значит 1016: 127 = 8.

При делении на двух- и трехзначное число в случаях, когда в част­ном получается не одна цифра, проще ориентироваться при подборе пробной цифры частного на первые цифры делимого и делителя.

Первое неполное делимое — 818 десятков, значит, в частном бу­дет две цифры — десятки и единицы.

Первая цифра делимого 8, первая цифра делителя 3, делим 8:3, можно взять по 2. Проверяем первую пробную цифру частного 341 • 2 = 682. Находим остаток 818 - 682 = 136 < 341, значит, цифра 2 подходит.

Второе неполное делимое 1364, первая цифра 1, но она на 3 не разделится. Значит, делим 13 на 3. Можно взять по 4. Проверяем вторую пробную цифру частного 341 • 4 = 1364. Значит, 4 подхо­дит. Деление закончено.

Ответ 24.

Пробная цифра частного проверяется устно, и в этом основная трудность деления на двузначное и трехзначное число. Если ре­бенок не владеет приемами, облегчающими поиск и первичную проверку пробных цифр частного, то он каждый раз умножает на пробную цифру частного весь делитель, что является сложным и трудоемким процессом, который невозможно выполнить без при­менения письменных алгоритмов умножения.

Письменные алгоритмы умножения и деления на двузначное и трехзначное число дети изучают в конце 4 класса, поэтому учитель не всегда успевает уделить им достаточно много времени. Большие затраты времени при непродуктивном поиске пробных цифр частного приводят к тому, что на одном уроке дети успевают решить 2—3 примера. Большее количество примеров может быст­ро привести к утомлению детей и соответственно большому ко­личеству ошибок при вычислениях. Использование продуктивных вычислительных приемов при выполнении письменных вычисле­ний поможет ребенку в овладении осознанной вычислительной деятельностью.