ЭД-103 / Subj / 1084-Линейная алгебра

									15; 6; 5		20; 3;16 . Найти:
Задача 3. Даны векторы a										b
1)	a b a ;
2)		a		;
3)	cos a, с , если c 2a b ;
4)	cos для a ;
5)		a b				;

6) пр b a .

Решение

1) вычислим a b a .

																																																		x1			x2 ; y1 y2 ; z1 z2 .
		Разность двух векторов определяется по формуле: a																																												b
Тогда b a 20 15; 3 ( 6);16 ( 5) 5; 9; 21 .
		Скалярным произведением двух векторов a и b называется число, обозначаемое a																																																										b и
																															x1 , y1 , z1 ,												x2 , y2 , z2 ,
равное		a	b						a				b		cos(a,b) . Если														a												b												то скалярное произведение
																																			x1x2						y1 y2 z1z2 .
двух векторов определяется по формуле:																																a	b
		Тогда								a b a 15 5 ( 6) 9 ( 5) 21 84 .
2) вычислим									a			.
																						x1, y1, z1						в прямоугольных декартовых координатах вычисляется по
		Длина вектора
																			a
формуле:				a								x2 y2						z2				. Тогда						a			152			( 6)2							( 5)2							225 36 25 286 .
												1				1				1
																		, если c 2a b .
3) вычислим cos a, с
		Вектор c 2a b 2 15; 6; 5 20; 3;16 50; 9; 6 .
																																x1x3 y1 y3 z1z3
																								a c
		По формуле cos a, с																																																вычислим
																								a		c				x1 y1					z1						x3		y3 z3
																													2					2		2				2			2			2
												15				50 ( 6) ( 9) ( 5) 6																									750 54 30													774
cos a, с																																																									.
			15									( 6)							( 5)							50			( 9)					6								286				2617							748462
										2							2						2					2					2			2

4) вычислим cos для a . Направление вектора определяется углами α, β, γ, образованными с

осями координат Ox, Oy, Oz. Косинус угла β определяются по формуле: cos		y1
			.
		a

y2

6

Тогда cos

.

a

286

5)

вычислим

a b

.

a b 35; 3; 9 .

Сумма векторов равна вектору с координатами:

вектора равна

a b

352 ( 3)2 92

1225 9 81 1315 .

6)

вычислим пр b a .

Проекцией

вектора

число, равное

a

на вектор b называется

Тогда длина этого

		a	b
пр a					. Тогда
b			b

						15 20 6 3 5 16					202
		a	b
пр a														.
b			b				202 32	162			665

Тема 4. Уравнения прямой на плоскости

Опр. Всякий ненулевой вектор, коллинеарный данной прямой, называется ее направляющим вектором.

Опр. Если вектор		перпендикулярен направляющему вектору		прямой l, то он называется
	n		а

нормальным вектором прямой l.

1) каноническое уравнениями прямой, проходящей через точку М0(x0, y0) и имеющей

направляющий вектор		а1, а2 :
	а

x x0

y y0

1

a1

a2

2) уравнение прямой, проходящей через две точки М0(x0, y0)

и М1(x1, y1):

x x0

y y0

2

y

x x

0

y

0

1

1

3)

общее уравнение прямой

на плоскости.

Вектор a B, A является направляющим

вектором прямой, а вектор

заданной

n А, В является нормальным вектором прямой,

общим уравнением:

Ax By C 0

(3)

4)

уравнением прямой, проходящей

через

точку

М0(x0,

y0) перпендикулярно

вектору

n А, В :

А x x0 ) В( y y0 0

(4)

5)расстояние d от точки М0(x0, y0) до прямой, заданной общим уравнением вычисляется формулой:

d

Ax0 By0 C

(5)

A2 B 2

6) расстояние d между двумя точками М0(x0, y0)

и М1(x1, y1) вычисляется по формуле:

d

x1

x0 2

y1 y0 2

(6)

7) координаты точки М(x, y), делящей отрезок М1М2

пополам вычисляется по формуле:

x1

x2

x

2

(7)

y1

y2

y

2

8) условие перпендикулярности прямых: прямые l1

и l2 перпендикулярны, если нормальные

векторы n1 A1, B1 и n2 A2 , B2 ортогональны, т.е. A1 A2 B1 B2 0 .

9) условие параллельности прямых: прямые l1 и l2 параллельны, если их направляющие

	B1, A1				B2 , A2			коллинеарны, т.е. координаты этих векторов
векторы a		и b
пропорциональны:			А1			В1	.
			А2			В2

Задача 4. Известны координаты вершин треугольника ABC: A(4; 3); B(-3; –3); C(2; 7). Найти:

1)общее уравнение всех сторон;

2)уравнение всех высот в общем виде (AN1, BN2, CN3);

3)уравнение всех медиан в общем виде (AM1, BM2, CM3);

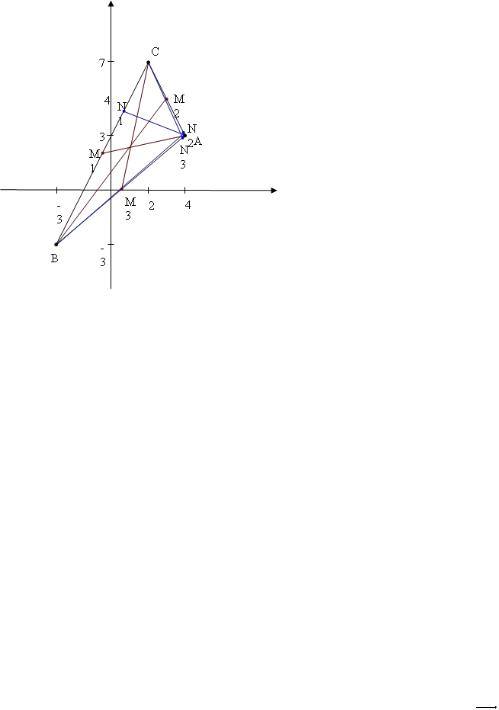
4)расстояние от точки C до прямой AB;

5)уравнение прямой CC1, проходящей параллельно AB;

6)длину стороны AB;

7)длину медианы AM1;

8)длину высоты AN1;

9)площадь треугольника ABC.

Решение.

1) Найдем общее уравнение всех сторон.

Найдем уравнение стороны AB как уравнение прямой, проходящей через две точки A(4; 3) и

B(-3; –3) согласно формуле (2):

y 3

x 4

y 3

x 4

- 7 y - 3 ( 6)(x 4) 6x - 7y - 3 0 .

3 3

3 4

6

7

Найдем уравнение стороны BС как уравнение прямой, проходящей через две точки B(-3; –3)

и C(2; 7):

y 3

x 3

y 3

x 3

5 y 3 10(x 3) 2x - y 3 0 .

7 3

2 3

10

5

Найдем уравнение стороны AС как уравнение прямой, проходящей через две точки A(4; 3) и

C(2; 7):

y 3

x 4

y 3

x 4

- 2 y - 3 4(x 4) 2x y -11 0 .

7 3

2 4

4

2

2) Найдем общее уравнение всех высот (AN1, BN2, CN3).

Найдем общее уравнение высоты AN1

как уравнением прямой, проходящей через точку

М0(x0, y0) перпендикулярно нормальному вектору n А, В . Так как прямая проходящая

через точку А(4, 3) перпендикулярно

нормальному вектору BC 5,10 , то уравнение

данной прямой будет иметь вид:

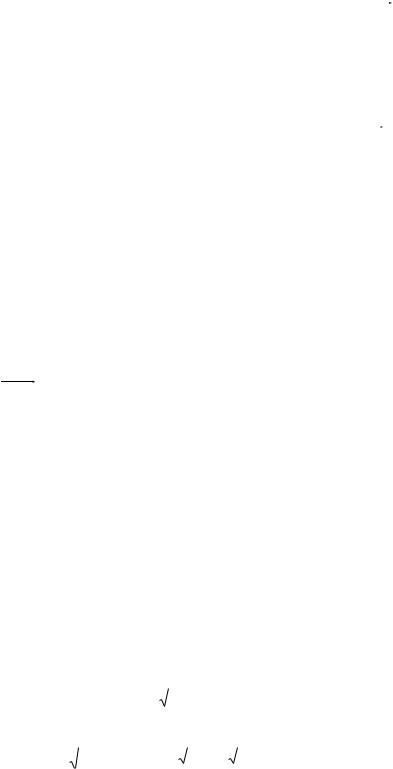
5 x 4) 10( y 3 0 5x 20 10y 30 0 5x 10y 50 0 x 2y 10 0 .

Найдем общее уравнение высоты BN2 как уравнением прямой, проходящей через точку через точку B(-3, -3) перпендикулярно нормальному вектору AC 2,4 , то уравнение данной прямой будет иметь вид:

2 x 3) 4( y 3 0 2x 6 4y 12 0 2x 4y 6 0 x 2y 3 0 .

Найдем общее уравнение высоты CN3 как уравнением прямой, проходящей через точку через точку C(2, 7) перпендикулярно нормальному вектору AB 7, 6 , то уравнение

данной прямой будет иметь вид:

7 x 2) 6( y 7 0 7x 14 6y 42 0 7x 6y 56 0 7x 6y 56 0. .

3)Найдем уравнение всех медиан в общем виде (AM1, BM2, CM3).

Чтобы найти уравнение медианы AM1, нужно найти координаты точки M1 - середины

отрезка ВС, по формуле (7) имеем: х								х1 х2			;	у	у1 у2	.
													2
										2
Тогда х	2 3		1	;	у	7 3	2 М			( 0,5;2) .
									1
2		2			2

Пусть a AМ1 4,5; 1 – направляющий вектор прямой.

Тогда из канонического уравнения прямой на плоскости (1) имеем:

х x1

у y1

.

a1

a2

Следовательно,

х 4

у 3

AМ1 :

2x 9y 19 0.

4,5

1

Аналогично уравнение

медианы

BM2

в общем виде:

4x 3y 3 0 , медианы

СM2: 14x 3y 7 0.

4) Найдем расстояние от точки C до прямой AB.

Расстояние от точки C(2; 7) до прямой AB, заданной общим уравнением

6x - 7y - 3 0

вычисляется формулой (5): d

Ax3 By3

C

.

A2 B 2

Следовательно, d

40

40

.

6 2 7 7 3

62 ( 7)2

85

85

5) Найдем уравнение прямой CC1, проходящей параллельно AB.

Прямая СС1 проходит через точку C(2; 7) и параллельна AB, заданной общим уравнением

6x - 7y - 3 0 . Таким образом, прямая CC1, заданная общим Ax + By + C = 0 и параллельна прямой AB, если ее коэффициенты при x и y пропорциональны (согласно условию

параллельности

прямых), т.е.

A

B

.

Взяв

A = 6,

B

=

-7

(при

коэффициенте

6

7

пропорциональности,

равном

1),

получим

уравнение

прямой

CC1: 6x - 7y С 0 .

Коэффициент

С найдем с учетом того, что координаты точки С(2;7), лежащей на прямой,

должны удовлетворять ее уравнению, т.е.

6 2 - 7 7 С 0 ,

откуда С =

37 и уравнение

прямой СС1 примет вид: 6x - 7y 37 0.

6) Найдем длину стороны AB.

Длина стороны AB – это расстояние от точки А до точки

B и находится по формуле (6):

x2 x1 2 y2

y1 2

, тогда

3 4 2 3 3 2

AB

AB

85.

7) Найдем длину медианы AM1.

Длина медианы AM1 – это расстояние от точки А до точки

М1 ( 0,5;4)

и находится по

формуле (6):

0,5 4 2

3 4 2

AМ1

21,25.

8) Найдем длину высоты AN1.

Длина высоты

AN1 – это расстояние от точки А(4;3) до прямой BC и вычисляется по

формуле (5):

d

Ax1 By1 C

.

Так как

общее уравнение

прямой

BC имеет вид

A2 B 2

2x - y 3 0 , то d

2 4 1 3 3

8

8

.

22 ( 1)2

5

5

9)Найдем площадь треугольника ABC.

Площадь треугольника вычисляется по формуле: S 12 AB AC

Имеем AB 7; 6;0 , AC 2;4;0 .

				i
	Тогда		AB AC		7
		q
					2

j	k	k ( 1)1 3		7	6		( 28 12)k 40k .
6	0
4	0			2	4

											0,0, 40 .
	Следовательно, вектор q
				1				1					1
	Тогда S								0		2 02 ( 40)2			40	20 (кв. ед.)
						q
				2				2					2

Список литературы

1.Высшая математика для экономистов: учеб. для вузов / под ред. Н.Ш. Кремера. - 3-е

изд. - М.: ЮНИТИ-ДАНА, 2009. - 480 с.

2.Практикум по высшей математике для экономистов: учеб. пособие для вузов / под ред.

Н.Ш. Кремера. - М.: ЮНИТИ, 2005. - 423 с.

3.Карасев А.И. Курс высшей математики для экономических вузов: в 2 ч.: учеб. пособие для вузов / А.И. Карасев, З.М. Аксютина, Т.И. Савельева. - Ч. 2: Теория вероятностей и математическая статистика. - М.: Высшая школа, 1982. - 320 с.

4.Красс М.С. Основы математики и ее приложения в экономическом образовании : учеб.

для вузов / М.С. Красс, Б.П. Чупрынов. - М.: Дело, 2001. - 688 с.

5.Григулецкий В.Г. Высшая математика для экономистов: учеб. пособие для вузов / В.Г.

Григулецкий, З.В. Ященко. - Ростов-на-Дону: Феникс, 2004. - 640 с.

6.Линьков В.М. Высшая математика в примерах и задачах: компьютерный практикум:

учеб. пособие для вузов / В.М. Линьков, Н.Н. Яремко; под ред. А.А. Емельянова. - М.:

Финансы и статистика, 2006. - 320 с.

7.Владимирский Б.М. Математика. Общий курс: учеб. для вузов / Б.М. Владимирский,

А.Б. Горстко, Я.М. Ерусалимский. - СПб.: Лань, 2002. - 960 с.

8.Ильин В.А. Высшая математика: учеб. для вузов / В.А. Ильин, А.В. Куркина. - 2-е изд.,

перераб. и доп. - М. : Проспект, 2004. - 593 с.

9.Клюшин В.Л. Высшая математика для экономистов: учеб. пособие для вузов / В.Л.

Клюшин. - М.: ИНФРА-М, 2006. - 448 с.

10.Коршунова Н.И. Математика в экономике: учеб. пособие / Н.И. Коршунова, В.С.

Плясунов. - М.: Вита, 1996. - 368 с.

11.Кострикин А.И. Введение в алгебру: учеб. для вузов / А.И. Кострикин. - Ч. 2:

Линейная алгебра. - 2-е изд., испр. - М.: Физматлит, 2001. - 368 с.

12.Малугин В.А. Математика для экономистов. Линейная алгебра: курс лекций : учеб.

пособие для вузов / В.А. Малугин. - М.: ЭКСМО, 2006. - 218 с.

13.www.intuit.ru/ - INTUIT.ru: Интернет Университет Информационных Технологий -

бесплатное дистанционное образование компьютерным дисциплинам.

14.Электронное учебное пособие по выполнению практических работ http://223.254.254.3/network/edu/default.asp.

Приложение 1

Индивидуальные задачи

Тема 1. Действия с матрицами

Задача 1. В вариантах 1-10 найти значение выражения 3BA + CB; в вариантах 11-20 найти значение выражения BA + 2CB; в вариантах 21-28 найти значение выражения 2BA – CB.

1.			1	2	3			1 0			2			1		2
	А
			0 1 3 , B									, C
			1 2 1					0 2			1			0		1
2.			5	2		1		0 3			2			5		2
	А		3 1
						4 , B						, C
											1				3
								1 2								1
			2	7		0
3.			1		4	3			3		1 2					1	4
	А		3		2
						2 , B							, C
										1 2 0							2
			5													3
					4	0
4.			1		0	1		1		1 4					1	0
	А		3
					2 2 , B							, C
			2		4				2		1 0				3	2
						0
5.			2		2	1		3 0			2				2	2
	А		1
					3 1 , B							, C
			1 0			1		1 1			2				1	3
6.			0		2	2			1 0			2				0		2
	А		5		2
						4 , B							, C
										1	4 1								2
																5
			3		1	5
7.			1		1	1			3		0 0					1 1
	А		7		4
						3 , B						, C
			5		2 1				0		1 3					7	4
8.			3	2	5			2	3		0			3		2
	А
			5 7 3 , B								, C
								2 1			1			5		7
			3	1	5
9.			1	3		7		3 1			2			1		3
	А		2	7
						1 , B						, C
										1 2					2
				2				0								7
			0			4
10.			7		2	2		1 2 1							7	2
	А		1		1
						3 , B						, C
									0
			5								1 1				1	1
					9	3

11.		1		9		0					2 3
	А		1					0						1			9
				4 1 , B									, C
									1		1 2
			3	2		2								1 4
12.			1		2		0
	А		3		7						1 3		4		1		2
							5 , B						, C
			5		4		1				2 1 0					3	7
13.		5			1		0							5 1
	А		2		1				1		3 2
							1 , B					, C
			5						0		1 2			2 1
					3		0
14.		0			1	2
	А		2		2				4		0 1			0			1
						9 , B							, C
										0							2
											1 2			2
			4		2	1
15.		3		7		5
	А		3					1			1	1		3			7
				4 0 , B									, C
									4
			0	2		1					0 1			3		4
16.			1		7	1		1 1
	А		4									0		1 7
					1 2 , B							, C
			5		2	0			1		0 5			4 1
17.		2		2	3			5			1 1
	А		1										2		2
				2 3 , B								, C
			1	1	1			0			2 1		1		2
18.		3		2		2
	А		3	2					0		2		1		3		2
						1 , B							, C
			1	1						4	1 1					3		2
						1
19.		0			2	5			1 2			1
	А		7		9									0			2
						3 , B							, C
										3					7
			1		1						0 1						9
						4
20.		6			5		3										5
	А		1		7				1		0 1			6
							5 , B						, C
																	7
									3		1 1			1
			0		4		1
21.		4		1		2						2
	А		2	3					1 3						4		1
						0 , B							, C
										1 0						2
													1				3
			3	1		2
22.		1			2	4
	А		1					3			1 1			1 2
					7 0 , B							, C
								0			3 1		1 7
			0		3	5
23.		2		1		1
	А		2	3					2		2		1	2			1
						0 , B							, C
			1	1 1					3		0 1			2				3

24.		2			7	5		1		2 1						7
	А		3		4									2
						0 , B					, C
									3					3		4
			2							0 2
					2	9
25.		1		2	3		2 2			1		1		2
	А		1	0
					4 , B						, C
								0 1
											2	1		0
			5	3		2
26.		4		1		2		1		1	1			4 1
	А		0	2
						7 , B					, C
									3	2				0 2
				2							1
			5			3
27.		1			4	2		4			0	1			4
	А		7		2					2
						1 , B					, C
									0	1						2
			3		4						1	7
						0
28.		1			2	0		0		1 3		1		2
	А		3
					2 3 , B						, C
														2
			5		1			1		2 0		3
						2