
- •Содержание
- •A. Найти производные от функций :
- •B. Найти производные от функций :
- •C. Найти производные от сложных функций :
- •Тема - исследование графика функции
- •A. Исследовать функции и построить графики :
- •Тема - неопределенный интеграл
- •A. Вычислить интегралы :
- •Тема – Несобственные интегралы
- •A. Вычислить интегралы или определить их расходимость :
C. Найти производные от сложных функций :
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Тема - исследование графика функции
Определение.
Функция![]() имеет экстремум ( максимум или минимум
) в точке
имеет экстремум ( максимум или минимум
) в точке![]() ,
если
,
если![]() является наибольшим или наименьшим
значением функции в некоторой двусторонней
окрестности этой точки.
является наибольшим или наименьшим
значением функции в некоторой двусторонней
окрестности этой точки.
Необходимое
условие существования экстремума.
Функция![]() имеет экстремум в точке
имеет экстремум в точке![]() ,
если первая производная функции
,
если первая производная функции![]() в этой точке равна нулю
в этой точке равна нулю![]() или не существует.
или не существует.
Достаточные
условия существования экстремума.
Если функция![]() непрерывна в точке
непрерывна в точке![]() и имеет в некоторой окрестности
и имеет в некоторой окрестности![]() кроме, может быть, самой точки
кроме, может быть, самой точки![]() ,
конечную производную и если при переходе
через
,
конечную производную и если при переходе
через![]() :
:
 меняет свой знак
с + на -, то точка
меняет свой знак
с + на -, то точка
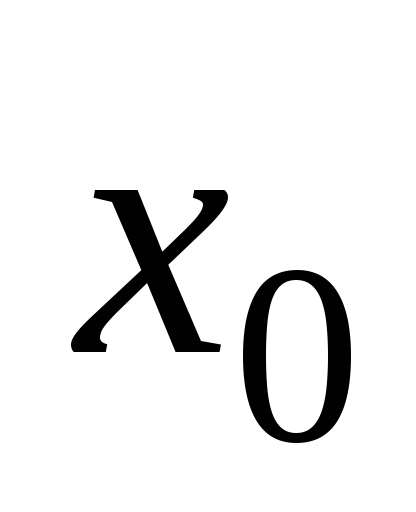 -
точка максимума ;
-
точка максимума ; меняет свой знак
с - на +, то точка
меняет свой знак
с - на +, то точка
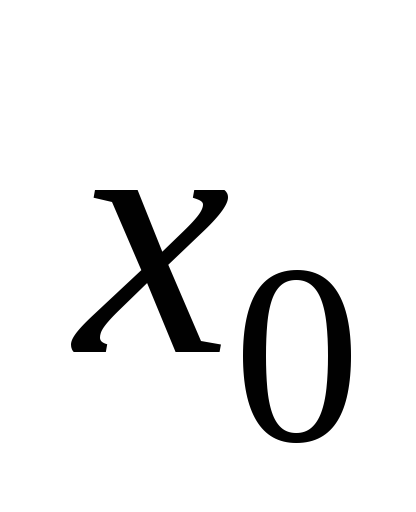 -
точка минимума ;
-
точка минимума ; не меняет знака,
то экстремума нет.
не меняет знака,
то экстремума нет.
A. Исследовать функции и построить графики :
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Тема - неопределенный интеграл
Определение.
Функция![]() называется первообразной для функции
называется первообразной для функции![]() на некотором промежутке, если для всех
значений
на некотором промежутке, если для всех
значений![]() из этого промежутка выполняется
равенство
из этого промежутка выполняется
равенство![]() .
.
Определение.
Неопределенным интегралом![]() называется множество всех первообразных
функций
называется множество всех первообразных
функций![]() для данной функции
для данной функции![]() (где
(где![]() - произвольная постоянная ) :
- произвольная постоянная ) :
![]()
Отыскание неопределенного интеграла по данной подинтегральной функции или восстановление функции по ее производной называется интегрированием этой функции.
Одним из приемов для интегрирования функций является метод, основанный на следующей формуле :
![]() ,
,
где
![]() и
и![]() -
функции, имеющие непрерывные производные
-
функции, имеющие непрерывные производные![]() и
и![]() .
Формула называется формулой интегрирования
по частям неопределенного интеграла.
.
Формула называется формулой интегрирования
по частям неопределенного интеграла.
A. Вычислить интегралы :
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
B. Вычислить интегралы, используя замену переменной :
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
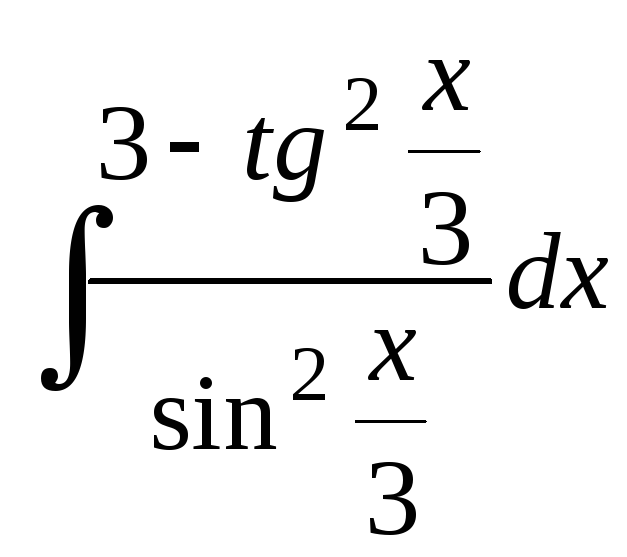
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
C. Вычислить интегралы по частям :
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
D. Вычислить интегралы от дробно-рациональных функций :
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
тема - определенный интеграл
Определение.
Определенным интегралом функции![]() на интервале
на интервале![]() называется число, которое может быть
найдено по формуле Ньютона-Лейбница :
называется число, которое может быть
найдено по формуле Ньютона-Лейбница :
![]() ,
,
где
![]() некоторая первообразная функции
некоторая первообразная функции![]() на интервале
на интервале![]() .
.
A. Вычислить интегралы :
1.

2.
![]()
3.
![]()
4.
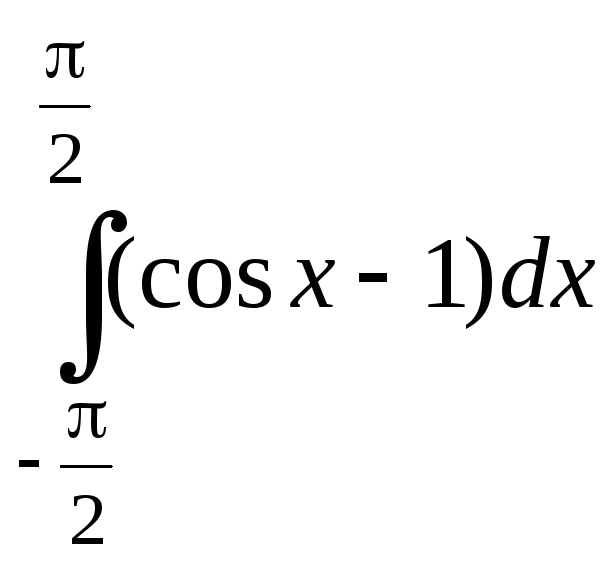
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
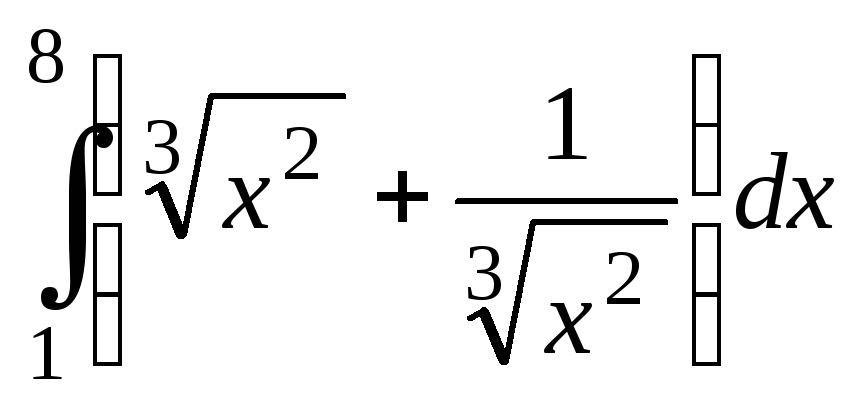
14.
![]()
15.
![]()
16.
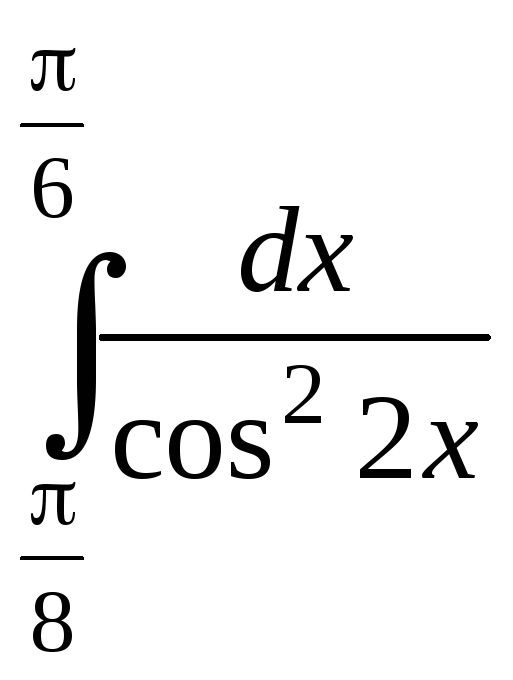
17.
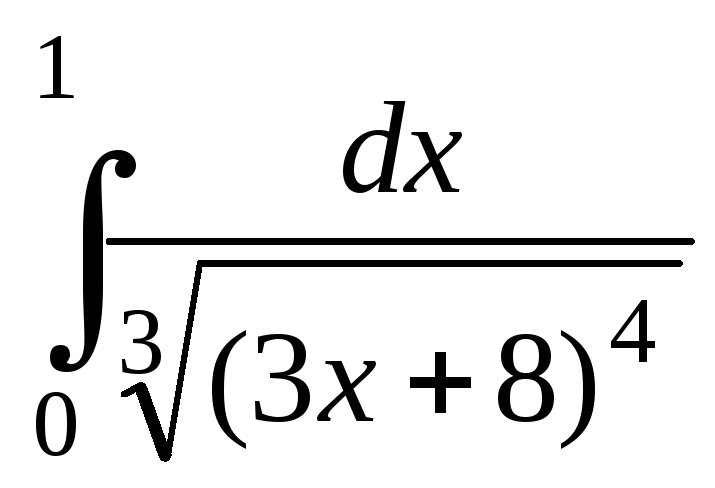
18.
![]()
19.
![]()
20.
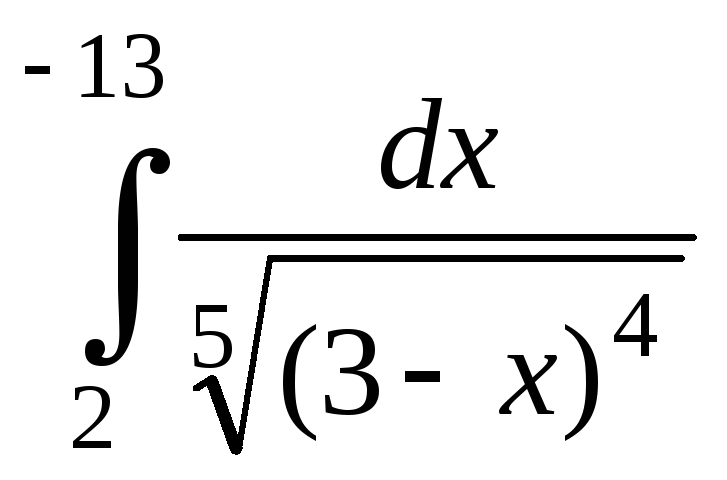
21.
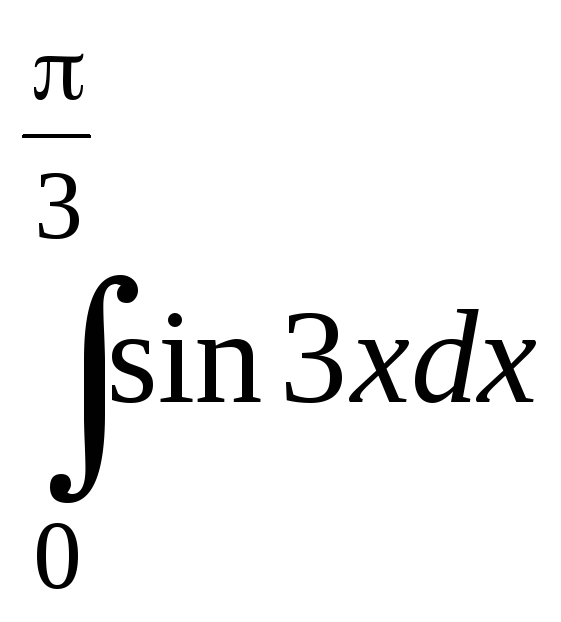
22.
![]()
23.
![]()
24.
![]()
25.

26.
![]()
27.
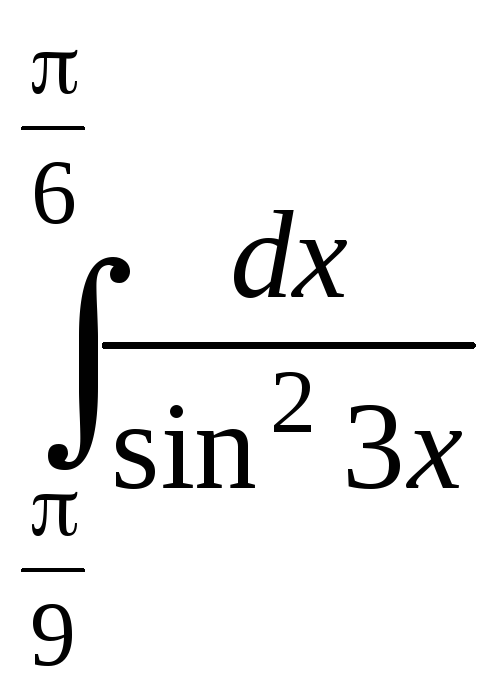
28.
![]()
29.
![]()
30.
![]()
B. Вычислить интегралы по частям и от дробно-рациональных функций :
1.
![]()
2.
![]()
3.
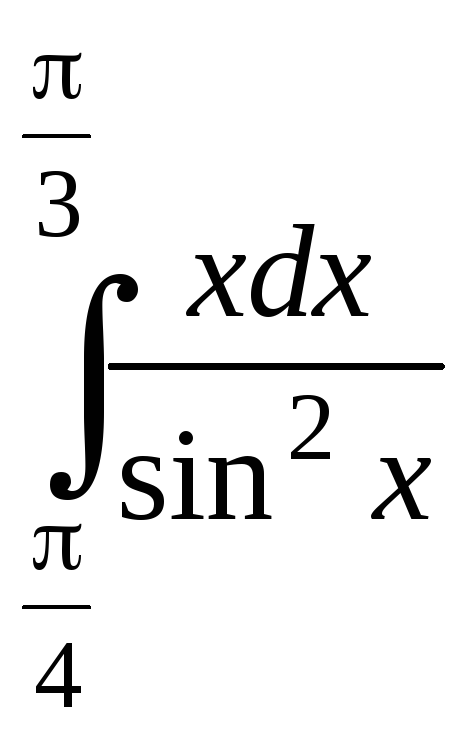
4.
![]()
5.
![]()
6.
![]()
7.
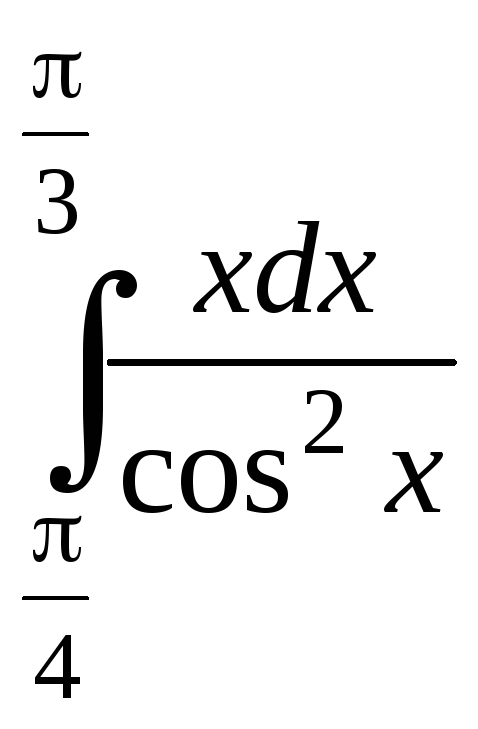
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
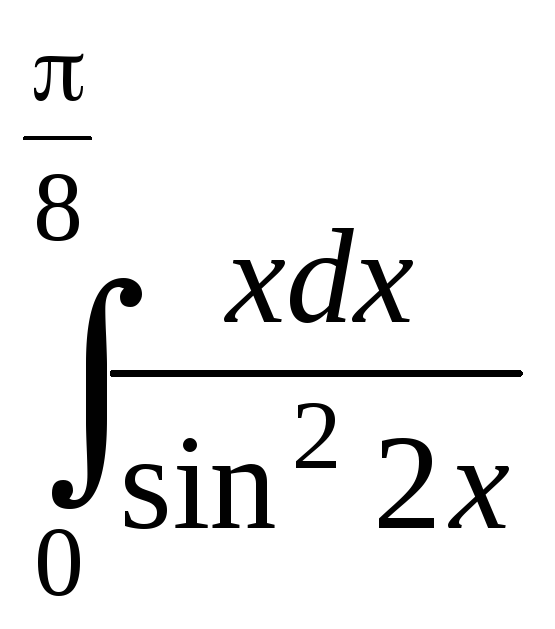
13.
![]()
14.
![]()
15.
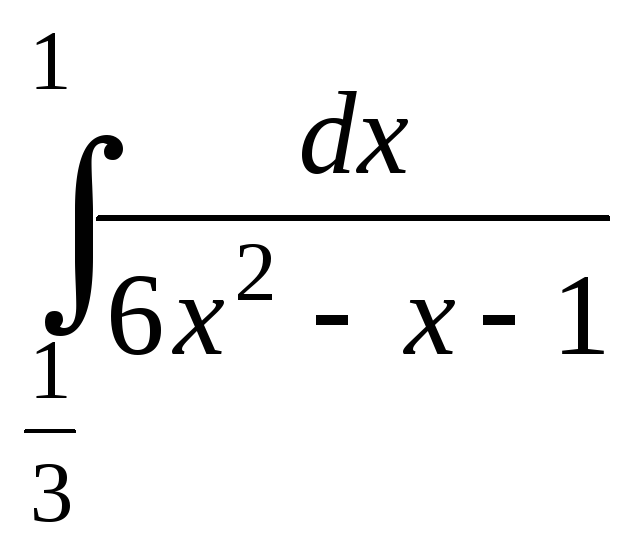
16.
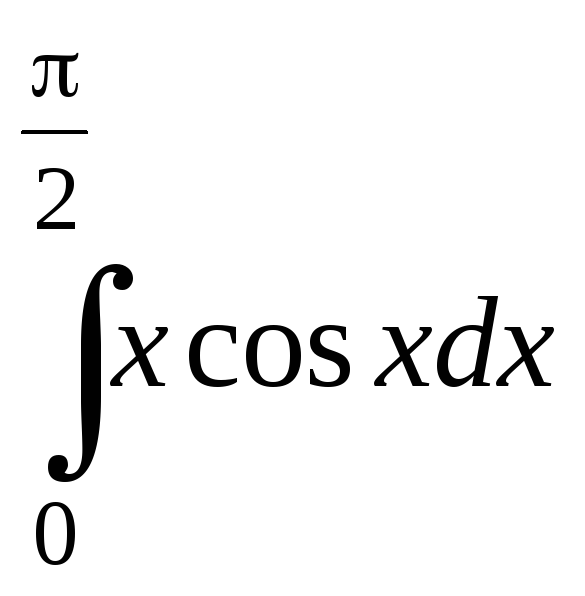
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
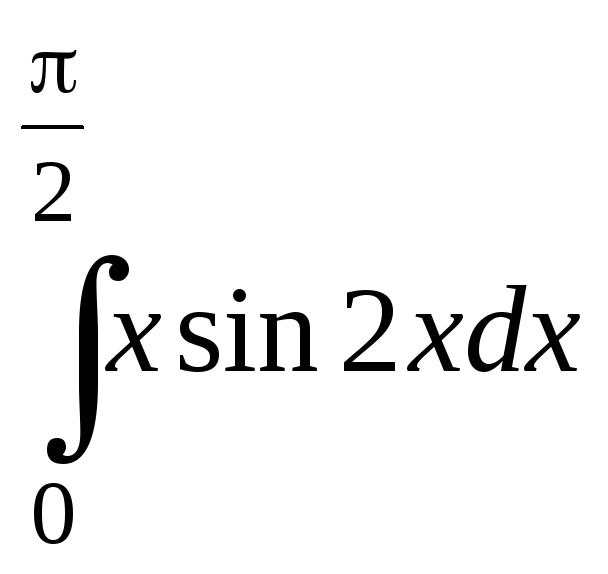
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
тема – приложения определенного интеграла
Площадь фигуры,
ограниченной графиком функции
![]() ,
осью ОХ и прямыми
,
осью ОХ и прямыми![]() и
и![]() ,
равна
,
равна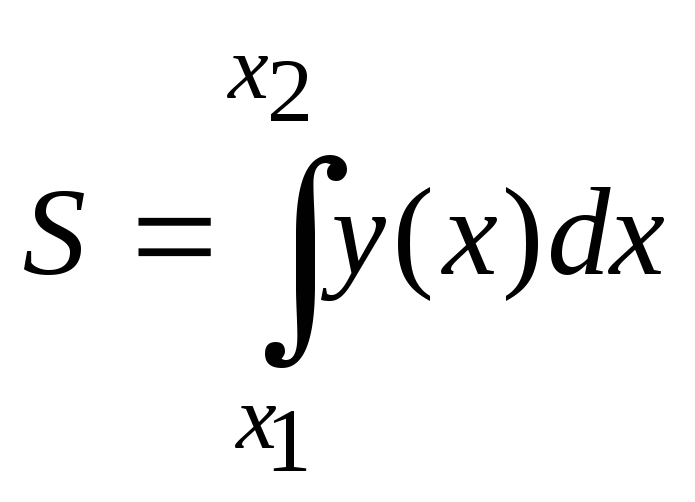
Площадь фигуры,
ограниченной графиком функции
![]() ,
осью ОУ и прямыми
,
осью ОУ и прямыми![]() и
и![]() ,
равна
,
равна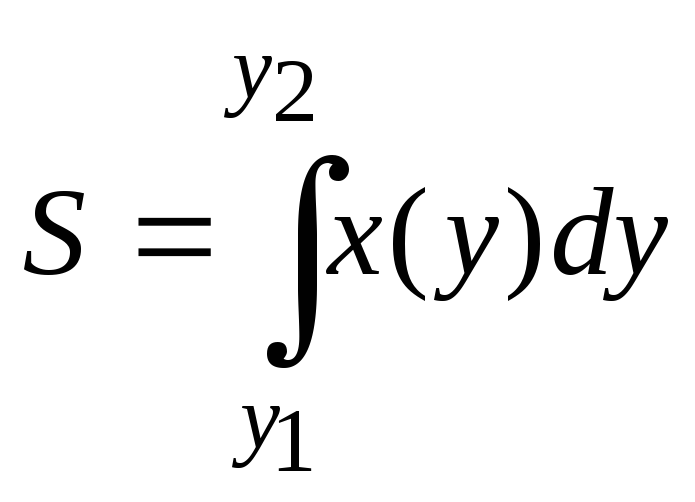
Объем тела,
образованного вращением фигуры,
ограниченной графиком функции
![]() ,
осью ОХ и прямыми
,
осью ОХ и прямыми![]() и
и![]() ,
равен
,
равен
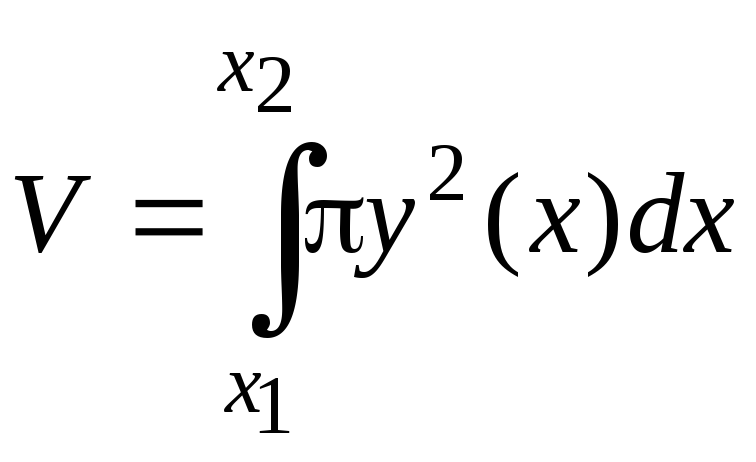
Объем тела,
образованного вращением фигуры,
ограниченной графиком функции
![]() ,
осью ОУ и прямыми
,
осью ОУ и прямыми![]() и
и![]() ,
равен
,
равен

A. Вычислить площадь фигуры, ограниченной линиями :
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
29.
![]()
30.
![]()
B. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями :
1.
![]() вокруг оси ОУ
вокруг оси ОУ
2.
![]() вокруг оси ОХ
вокруг оси ОХ
3.
![]() вокруг оси ОХ
вокруг оси ОХ
4.
![]() вокруг оси ОХ
вокруг оси ОХ
5.
![]() вокруг оси ОУ
вокруг оси ОУ
6.
![]() вокруг оси ОХ
вокруг оси ОХ
7.
![]() вокруг оси ОУ
вокруг оси ОУ
8.
![]() вокруг оси ОУ
вокруг оси ОУ
9.
![]() вокруг оси ОХ
вокруг оси ОХ
10.
![]() вокруг прямой
вокруг прямой![]() при
при![]()
11.![]() вокруг оси ОУ
вокруг оси ОУ
12.
![]() вокруг оси ОХ при
вокруг оси ОХ при![]()
13.
![]() вокруг оси ОХ
вокруг оси ОХ
14.
![]() вокруг оси ОУ
вокруг оси ОУ
15.
![]() вокруг оси ОХ
вокруг оси ОХ
16.
![]() вокруг прямой
вокруг прямой![]()
17.
![]() вокруг оси ОХ
вокруг оси ОХ
18.
![]() вокруг оси ОХ
вокруг оси ОХ
19.
![]() вокруг оси ОХ
вокруг оси ОХ
20.
![]() вокруг оси ОХ
вокруг оси ОХ
21.
![]() вокруг оси ОХ
вокруг оси ОХ
22.
![]() вокруг оси ОХ
вокруг оси ОХ
23.
![]() вокруг оси ОУ
вокруг оси ОУ
24.
![]() вокруг оси ОУ
вокруг оси ОУ
25.
![]() вокруг оси ОУ
вокруг оси ОУ
26.
![]() вокруг оси ОХ
вокруг оси ОХ
27.
![]() вокруг оси ОУ
вокруг оси ОУ
28.
![]() вокруг оси ОУ
вокруг оси ОУ
29.
![]() вокруг оси ОХ
вокруг оси ОХ
30.
![]() вокруг оси ОХ
вокруг оси ОХ
