01_-_mnozhestva_otobrazhenia_logika

1. НАЧАЛЬНЫЕ ПОНЯТИЯ И МОДЕЛИ

1.1. МНОЖЕСТВА

1.1.1. ПОНЯТИЕ МНОЖЕСТВА

Множеством называется всякая совокупность объектов.

При этом, как правило, можно указать общее свойство, которым обладают или которым характеризуются элементы, входящие во множество. Например, множество писателей, книги которых имеются в продаже в некотором магазине. Элементами данного множества являются люди, характеризующиеся общим свойством : авторы книг, продаваемых в данном магазине.

Множествами можно также считать следующие совокупности:

1)всех рек, впадающих в Черное море ;

2)видов птиц, гнездящихся на данной территории ;

3)сортов картофеля, районированных в некотором

регионе;

4)студентов первого курса факультета прикладной математики.

Математика имеет дело со специальными множествами такими, как множество точек на плоскости, множество простых чисел, множество решений некоторого уравнения, множество монотонно возрастающих числовых функций.

Для обозначения множеств в математике принято

использовать прописные символы. Объекты, входящие во множества или элементы множеств, обозначаются с помощью строчных символов.

Пусть элемент a входит в некоторое множество A. Данный

факт будем записывать с помощью выражения: a A. Здесь специальный символ прина длежности элемента множеству, а

запись a A понимается как "a является элементом множества

A" или "элемент a принадлежит множеству A".

Если объект a не содержится во множестве A, то запись этого факта имеет вид : a A.

5

Среди множеств особое место занимает множество, не содержащее ни одного элемента, которое называется пустым множеством и обозначается специальным символом .

Самое большое множество, состоящее из всех возможных

элементов, называется Универсумом и обозначается как U. Всякое конкретное множество является частью или подмножеством этого множества .

1.1.2. ПРЕДСТАВЛЕНИЕ МНОЖЕСТВ

Для представления или задания множеств используется несколько разных способов.

1. Непосредственное задание

Множества задаются перечислением всех входящих в них элементов, которые заключаются в фигурные скобки.

Например, множество областных и краевых центров юга России можно задать как {АСТРАХАНЬ, ВОЛГОГРАД,

КРАСНОДАР, РОСТОВ, СТАВРОПОЛЬ}.

Данный способ может использоваться и для задания множеств, содержащих бесконечное число элементов. В этом случае записывается несколько элементов таких множеств, после чего ставится многоточие, предполагающее, что понятно каким образом можно выписать и другие элементы данног о множества.

Например, множество всех целых неотрицательных чисел можно задать как: N = {0, 1, 2, ... }. Множество всех четных натуральных чисел может быть записано { 0, 2, 4, ... }, где многоточие понимается как слова " и так далее ".

2.Задание множества у казанием характеристического

свойства

В таком способе задания множеств используются записи в фигурных скобках.

Пространство между открывающей и закрывающей скобками делится на две части с помощью вертикальной черты.

Слева от разделителя записывается общ ий вид элементов множества, а справа свойство, которым обладают элементы данного множества и не обладают никакие другие элементы. Свойство элементов множества, указанное в задании множества, называется характеристическим свойством.

6

A, если

Например. Множество вс ех пар людей, знакомых между

собой, может быть задано так: {( x, y) | x знает y} это множество пар людей, первый из которых знает второго.

Множество { 2n | n N} это множество всех четных натуральных чисел.

3. Задание множества указанием его имени

Например. Множество A, список № 5 или 5-й класс А средней школы № 1.

Данный способ удобен, когда множество рассматривается целиком как совокупность объектов, обладающих общим свойством.

4. Задание множеств с помощью диаграмм Венна

Диаграммы Венна представляют собой наглядный способ одновременного задания нескольких произвольных множеств. При этом всякое множество представляется областью на плоскости, ограниченной замкнутой линией. Обычно такие области ограничиваются линиями, подобными окру жностям.

В изображении нескольких множеств на диаграммах Венна представляется их возможное взаимное сорасположение. Общие части замкнутых областей для множеств задают общие части соответствующих множеств. В частности, эти части могут быть пустыми.

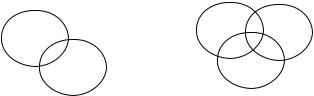
Например, диаграммы Венна для произвольных двух и трех множеств имеют вид:

A A C

B B

Множество B называется подмножеством множества каждый элемент множества B является элементом множества A.

Если B является подмножеством A, то в этом случае говорят о

включении	B	в	A и используют	символическое обозначение
B A, где			символ включения	множеств. Пусть B A и

дополнительно известно, что A не содержится в B. В этом случае говорят, что множество B строго включено во множество A. Для

7

A U B.

Объединением множеств

обозначения строгого включения множеств используют специальный символ .

Заметим, что для любого множества A справедливо включение: A.

Множества называются равными, если они состоят из одних и тех же элементов. Очевидно, что множества A и B являются равными тогда и только тогда, когда A B и B A.

1.1.3. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

Пусть A и B некоторые множества. Над этими множествами могут выполняться следующие основные операции.

1. Объединение множеств

A и B называется м ножество C,

определяемое соотношением: { x | x A или x B}, т.е. в объединение двух множеств входят те и только те элементы, которые содержатся хотя бы в одном из объединяемых множеств. Для обозначения операции пересечения используется специальный

символ U , а объединение множеств A и B записывается как

Диаграмма Венна для объединения множеств имеет вид :
A	A	B
	A U B
2. Пересечение множеств
Пересечением множеств A и B называется множество			{ x
| x A и x B}, т.е.	в пересечение двух множеств A и B входят

только такие элементы, которые содержатся в обоих множествах. Для обозначения операции пересечения используется специальный

символ , а пересечение множеств A и B записывается как A B. Соответствующая диаграмма Венна имеет вид:

A B

A B

8

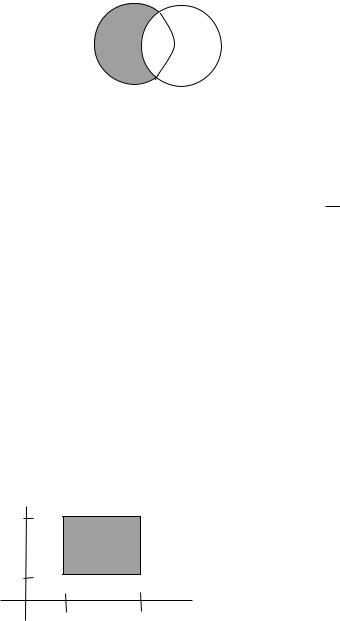
3. Разность множеств

Разностью множеств A и B называется множество:

{x | x A и x B}, т.е. в разность множеств A и B входят только

те элементы A, которые не содержатся в B. Для обозначения операции разности множеств используется специальный символ \, а разность множеств A и B записывается как A \ B.

Диаграмма Венна для разности множеств A и B имеет вид:

A B

A \ B

В определенных случаях приходится рассматривать все возможные элементы или объекты, которые не содержатся в

некотором множестве A. Для такой ситуации разность межд у Универсумом U и данным множеством A называется дополнением множества A. Дополнение A обозначается как A.

4. Произведение множеств

Произведением множеств A и B называется множество {(x, y) | x A и y B}, т.е. A B состоит из всевозм ожных пар элементов, в которых первая компонента является элементом A, а вторая элементом B. Для обозначения операции произведения множеств используется специальный символ , а произведение A и

B обозначается как A B.

Операцию произведения множеств мож но продемонстрировать на примере произведения двух подмножеств множества вещественных чисел, представляемых отрезками на числовой оси.

B

A

Здесь множества A и B представлены отрезками числовых осей. Тогда произведени е этих множеств это множество точек

9

плоскости, образующее прямоугольник, проекции которого на оси совпадают с отрезками, представляющими A и B.

Заметим, что если R это множество всех вещественных

чисел, то R R или R2 представляет собой множество всех пар вещественных чисел. Это множество принято отождествлять с двумерной координатной плоскостью.

Аналогично, R3 обозначает множество троек вещественных чисел. Это множество отождествляется с множеством точек в трехмерном пространстве.

5. Степень множества

Если A множество, то 2A обозначает множество всех

подмножеств множества A и называется степенью этого множества.

Упражнение.

1. Используя операции над множествами, выразить через

множества A, B и C множества 1 7 на следующей диа грамме Венна.

A 1 2 3 B

4 5 6

C 7

2. Проверьте справедливость тождеств ( A B) (C D) = (A C) (B D) и (A B) (C D) = (A C) (B D).

1.1.4. МОЩНОСТЬ МНОЖЕСТВ

Характеристика множ еств, представляющая количество содержащихся в них элементов, называется мощностью множеств.

Если некоторое множество A содержит конечное число

элементов, то его мощность | A| равна числу элементов этого множества. Для бесконечных множеств понятие количеств а элементов требует уточнения.

В общем случае понятие мощности произвольных множеств определяется через их равномощность.

ОПРЕДЕЛЕНИЕ

Множества A и B называются равномощными, если их элементы можно поставить во взаимно однозначное соответствие.

10

То есть мож но определить такое множество пар ( a, b), первая компонента которых принадлежит A, а вторая компонента принадлежит B. При этом для каждого a A существует одна пара, первая компонента которой равна a. Аналогично, для каждого элемента b B существует одна пара, вторая компонента которой равна b.

ОПРЕДЕЛЕНИЕ

Мощностью множества A называется семейство всех

множеств, равномощных A.

Поскольку всякое множество равномощно самому себе, то мощность всякого множества явля ется непустым семейством. Поэтому мощность является реальной характеристикой всякого множества. Мощность произвольного множества A обозначается символически как | A|.

Множество A конечно, если оно пустое или равномощно некоторому началу { 1, 2, ... , k} множества натуральных чисел N.

Для непустого конечного множества A, состоящего из k элементов, принято использовать число k в качестве обозначения мощности этого множества.

Мощность пустого множества считается равной нулю. Множество A называется счетно -бесконечным, если оно

равномощно множеству натуральных чисел N. Мощность счетнобесконечного множества обозначается как 0 .

Множество A называется счетным, если оно конечное или счетно-бесконечное. Содержательно счетность множества означает, что его элементы можно последовательно пересчитать подобно тому, как могут быть пересчитаны все элементы множества натуральных чисел. Для этого достаточно организовать пересчет N, при котором для каждого натурального числа указывается соответствующий ем у элемент счетного множества A.

Замечание. Счетные множества объектов это основной вид множеств объектов, изучаемых в дискретной математике .

Упражнение. Показать, что если A равномощно B, а B

равномощно C, то A равномощно C.

Рассмотрим некоторые свойства счетных множеств.

11

ТЕОРЕМА 1.1

Объединение любых двух счетных множеств является счетным множеством.

Доказательство

Пусть A и B счетные множества. Возможны следующие

случаи.
1	.	Если A и B конечные множества, то A B состоит из
конечного числа разных эл ементов, т.е. является счетным.
2	.	Если A конечное, а	B счетно-бесконечное, и

A={a1 , ... , ak }, B = {b1 , ... , bi , ...}, где элементы A и B

перечислены в порядке соответствия элементов A и B элементам множества { 1, ... , k} и множеству натуральн ых чисел соответственно.

Удалим из A элементы, содержащиеся в B. В результате получим новое множество { aj 1, ... , aj l}, которое может оказаться пустым.

Тогда множество { aj 1 , . . . , aj l , b1 , . . . , bi, ...}, в котором элементы перечислены в порядке соотве тствия возрастающим элементам множества натуральных чисел, является множеством,

равномощным N.

3. Множества A и B счетно-бесконечные. Тогда их можно

представить в виде:
A = {a1 , . . . , ai, . . .},	B = {b1 , . . . , bi , . . .}.

Рассмотрим процесс последовательного выписывания в один список первых, вторых, третьих и последующих элементов этих

множеств: a1		и b1 , a2	и b2 , a3 и b3 и т.д.
При этом в список не включаются такие из выбираемых
элементов, которые уже встречались ранее.
Этот	процесс		позволяет записать все элементы множества
A B	в	виде	счетной бесконечной последовательности

c1 , . . . , cj , . . . .

Такая последовательность содержит все элементы A B по одному разу, в сопоставлении их с натуральными числами, та к что элемент ci соответствует числу i.

Следовательно, A B является счетным множеством.

Доказательство окончено.

12

Упражнение. Доказать, что пересечение любых двух счетных множеств является счетным.

Нетрудно убедиться в том, что объединение и пересечение всякого конечного числа счетных множеств также является счетным множеством. В некоторых случаях приходится иметь дело с объединением или пересечением счетно -бесконечного семейства

счетных	множеств,	т.е.	рассматриваются	множества,
представляемые в виде: A = UA i .
		i N
Здесь	запись UA i	обозначает бесконечное		объединение
	i N

множеств A1 ... Ai ... При этом Ai = {ai 1, ... , aij, ...}.

Здесь aij j-й по порядку пересчета элемент множества Ai . Как следует из приводимой далее теоремы, такие множества

также оказываются счетными.

ТЕОРЕМА 1.2

Счетно-бесконечное объединение UA i счетных множеств i N

является счетным множеством.

Доказательство

Проведем доказательство для просте йшего случая, когда все множества Ai счетно-бесконечные и непересекающиеся. Остальные случаи могут быть предложены в качестве упражнения.

Выпишем элементы множества UA i в виде таблицы:

						i N
a 1 1		a1 2		a 1 3		. . .	a 1 j		. . .
a	2 1	a	2 2	a	2 3	. . .	a	2 j	. . .
a	3 1	a	3 2	a	3 3	. . .	a	3 j	. . .

.	.	.	. . .
.	.	.	. . .	.	. . .
a i 1	a i 2	a i 3	. .	. a i j	. . .
.	.	.	. . .	.	. . .
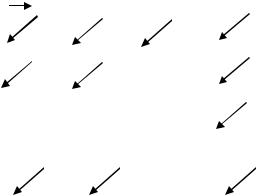
Последовательно пройдем по всем элементам таблицы в
порядке,	указанном	стрелками,		выписав	все	элементы

13

множества UA i . Элементы таблицы последовательно проходят по i N

диагоналям таблицы, начиная с левого верхнего угла, а на диагоналях - в направлении сверху вниз.

Такой пересчет элементов UA i ставит	их в однозначное
i N
соответствие элементам множества натуральных чисел.
Доказательство окончено.
Определим натуральное число n, равное порядковому
номеру элемента ai j в выписанном множестве	UA i .

i N

Отметим следующие свойства пересчета элементов:

1)число элементов i-й по порядку диагонали равно i;

2)при движении по диагонали сверху вниз первый индекс элементов возрастает, а второй убывает;

3)сумма индексов элемен тов i-й диагонали постоянна и равна i + 1.

Воспользуемся данными свойствами. Тогда справедливы следующие выводы:

а) элемент ai j находится на (i+j-1)–й, начиная от левого верхнего угла диагонали, поэтому число элементов диагоналей, предшествующих диагонали , содержащей ai j , равно:

1+ 2 + ... + i + j 2 = (i + j 1) (i + j 2) / 2;

b)элемент ai j является j-м по порядку элементом на диагонали с номером i + j 1.

Поэтому порядковый номер ai j в выписанном множестве

UA i равен: ((i + j 1) (i + j 2) / 2) + j . i N

Упражнение

1. Доказать справедливость последней теоремы для случаев,

когда множества Ai могут быть конечными или пересекающимися. 2. Доказать, что пересечение счетно -бесконечного семейства

счетных множеств является счетным.

ТЕОРЕМА 1.3

Для любого множества A множества A и 2A не являются равномощными.

14