17

ЛЕКЦИЯ 4

Содержание

1. Общие закономерности радиоактивного распада. Виды распада.

2. -Радиоактивность. Прохождение -частиц через барьер. Центробежный барьер.

3. -Распад. Нейтрино. Слабое взаимодействие. Промежуточные бозоны.

4. -Распад. Классификация фотонов. Правила отбора для электромагнитных переходов. Вероятности электромагнитных переходов в длинноволновом приближении.

5. Дополнительные выводы о -распаде. Разрешенные и запрещенные -переходы. Переходы Ферми и Гамова-Теллера.

1. Общие закономерности радиоактивного распада. Виды распада.

При ядерных превращениях или распадах происходят переходы между различными стационарными состояниями ядер. Ядро в возбужденном состоянии имеет среднее время жизни ™ Всякое возбуждение описывается волновой функцией, которая убывает со временем по закону

.

Уровень с имеет энергетическую неопределенность E=, которая связана с соотношением неопределенностей ( - ширина уровня на половине высоты). Наряду с используют понятие периода полураспада t_1/2 (half life) и константы распада . Е¸ смысл - вероятность распада ядра в единицу времени. Мы будем использовать обозначение w . t_1/2=ln2 - это время, за которое половина ядер испытывает распад.

Ядро может самопроизвольно переходить в более низкое состояние (при этом испускается -квант) или распадаться на различные конечные продукты. Необходимое условие такого превращения

,

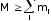ãäå m_i - масса i-го конечного продукта.

Определим энергию распада Q:

. (4.1)

Известны следующие виды распада:

- -распад (испускание ядер );

- -распад ();

- -распад;

- спонтанное деление;

- испускание нуклонов (1-го протона или нейтрона, 2-х протонов);

- испускание кластеров (ядер от ¹²C äî ³²S).

Ниже более подробно рассмотрим лишь , и - радиоактивность.

Области ядер с различным типом распада удобно показать на NZ-диаграмме (рис.2.1). Отклонение от области стабильности в сторону B_n=0 (нейтронно-избыточные ядра) приводит к ^--распаду (np+e^-+). Движение к линии B_p=0 (протонно-избыточные ядра) ведет к ⁺-распаду (pn+e⁺+) или e-захвату (p+e^-n+). Движение в сторону тяжелых ядер вдоль линии стабильности ведет к -распаду и спонтанному делению. Между линиями B_n=0 è B_p=0 5000-6000 ядер, живущих больше характерного ядерного времени _ÿ (10^-21-10^-23 сек), которое можно определить как время пролета испускаемой частицы через ядро. Для релятивистской частицы

_ÿ10^-22-10^-23 ñåê.

2. -Радиоактивность. Прохождение -частиц через барьер.

Центробежный барьер.

При Z>60 появляются нуклиды, нестабильные к -распаду. Самое легкое -радиоактивное ядро испускает -частицы с T=1.83 МэВ и t_1/2=2.410¹⁵ лет. Именно -распад обнаружил Беккерель в 1896 г. Условие -распада

M(A,Z) > M(A-4, Z-2) + M(4,2), M(4,2)=m.

Энергия -распада

Q=[M(A,Z) - M(A-4, Z-2) - m]c². (4.2)

Энергии -частиц заключены в основном в интервале 2-9 МэВ, а периоды полураспада в интервале 310^-7 ñåê () - 2.410¹⁵ ëåò (). Основная часть энергии -распада уносится -частицей и лишь 2% конечным ядром. Тонкая структура -спектров связана с образованием конечного ядра не только в основном, но и в возбужденных состояниях. Т.е. -спектры несут информацию об уровнях ядер (рис.4.1).

Ðèñ. 4.1

Вероятность -распада - произведение двух вероятностей - вероятности образования -частицы внутри ядра и вероятности покинуть ядро. Первый процесс - чисто ядерный. Его сложно рассчитать, т.к. ему присущи все трудности ядерной задачи. Второй процесс легко рассчитывается. Как будет видно из дальнейшего именно он, в основном, определяет время -распада.

Пусть внутри ядра двигается “готовая” -частица со скоростью v. В единицу времени она раз окажется на поверхности ядра и может в каждый из этих моментов покинуть его с вероятностью P.

Вероятность -частице покинуть ядро в единицу времени

w=P.

Рассмотрим потенциал, в котором движется -частица (рис.4.2). Это отрицательный ядерный потенциал притяжения (приблизительно прямоугольной формы) внутри ядра (r<R) и положительный потенциал кулоновского отталкивания вне ядра (r>R).

Ðèñ. 4.2

Отметим, что макси-мальная высота ку-лоновского барьера . Òàê, äëÿ = =35 ÌýÂ, à T2-9 ÌýÂ.

Возникает задача расчета вероятности проникновения через барьер. Без барьера -частица за характерное (ядерное) время 10^-21 сек (для T=5 МэВ) покинула бы ядро. Подчеркнем, что T - это кинетичиская энергия свободной -частицы (далеко за пределами ядра). Внутри ядра кинетическая энергия -частицы T+V₀.

Необходимо решить стационарное уравнение Шредингера для -частицы в центральном потенциале V(r)

, (4.3)

ãäå , где, в свою очередь, (лапласиан)=.

Вместо m нужно брать приведенную массу системы , где M - масса конечного ядра (без -частицы). В силу центральной симметрии удобно перейти к сферическим координатам x, y, z, r, , . По-существу задача свелась к написанию лапласиана в сферических координатах. Модифицируем уравнение Шредингера. Вместо оператора запишем классическое выражение для кинетической энергии

,

где v - скорость -частицы относительно ядра-остатка (скорость относительной частицы). В сферических координатах можно представить как векторную сумму радиальной () и угловой () скорости (рис.4.3).

Ðèñ. 4.3

Тогда , ãäå , L=vr, , v=r.

В свою очередь

; (4.4)

ãäå , à - энергия вращения (классическая). Учитывая, что момент инерции G точечной частицы равен r², легко получить более привычное выражение для этой энергии . Действительно, L²=(vr)²=²r⁴²=G²².

Подставив (4.4) в (4.3) и переходя к операторам, получаем

, (4.5)

ãäå - оператор в сферических координатах, причем

.

Очевидно имеет место уравнение

, (4.6)

ãäå - квантовомеханическая энергия вращения.

В сферических координатах угловые (, ) и радиальная (r) переменные в уравнении Шредингера разделяются и решение имеет вид

, (4.7)

ãäå Y_Lm(,) - сферические функции, для которых

L=0, 1, 2, ..., ; (4.8)

Y_Lm=mY_Lm m=L, (L-1), ..., 0.

Уравнение для u_L(r) имеет вид

, (4.9)

т.е. такой же, как одномерное уравнение Шредингера с эффективным потенциалом

V_ýôô = + V(r). (4.10)

Центробежная энергия , как и кулоновская V(r), препятствует вылету (сближению) -частицы из (и) ядра, увеличиваясь с уменьшением r, т.е. создает дополнительный (центробежный) барьер, который однако, мал (проценты от кулоновского).

Рассмотрим прямоугольный барьер и случай L=0 (центральный вылет или лобовой удар). Имеем

Ðèñ. 4.4

(4.11)

Уравнение (4.11) надо решить для областей 1, 2, 3:

u₁ = C₁e^ikr + D₁e^-ikr,

u₂ = C₂e^qr + D₂e^-qr, C₂=0 (4.12)

u₃ = C₃e^ikr + D₃e^-ikr, D₃=0.

, .

В области 3 решение C₃e^ikr отвечает частице, двигающейся вправо, т.е. в область r>R₀, à D₃e^-ikr - обратно (влево). Очевидно, надо положить D₃=0.

Решение C₂e^qr в области 2 не имеет смысла, т.к. отвечает растущей экспоненциально вероятности найти частицу с увеличением r.

В области 1 должна быть как падающая, так и отраженная от барьера волна.

Вероятность прохождения через барьер есть отношение вероятностей обнаружить частицу в точках R₀ и R. Для этого достаточно знания u(r) под барьером (область 2):

. (4.13)

Для определения вероятности проникновения через барьер произвольной формы, необходимо выполнить интегрирование

.

Для кулоновского барьера можно выполнить точное интегрирование и получить период полураспада

.

Это впервые сделал Гамов в 1928 г. еще до того как был открыт нейтрон (Гамов полагал, что ядро состоит из -частиц). При этом получается следующая приближенная формула

, (4.14)

где A150, а B55. Из этой формулы, в частности, следует, что при увеличении T от 4 до 9 МэВ, t_1/2 падает с 10²⁰ äî 10^-5 сек. Столь резкое падение t_1/2, очевидно вызвано тем, что кинетическая энергия -частицы входит в показатель экспоненты выражения для проницаемости барьера.

3. -Распад. Нейтрино. Слабое взаимодействие.