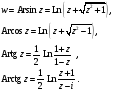- •Числовой ряд. Сумма числового ряда.
- •Необходимое условие сходимости числового ряда. Гармонический ряд.
- •Комплексная форма ряда Фурье.
- •Основные элементарные функции комплексной переменной.
- •26. Предел и непрерывность функции комплексной переменной.
- •35.Особые точки аналитических функций.
- •51. Применение формулы Дюамеля при решении задачи Коши.
-
Комплексная форма ряда Фурье.
Ряды
Фурье часто применяются в комплексной
форме записи. Преобразуем ряд
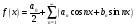 и его коэффициенты к комплексной форме.
Для этого используем формулы Эйлера,
выражение косинус и синус через
показательную функцию:
и его коэффициенты к комплексной форме.
Для этого используем формулы Эйлера,
выражение косинус и синус через
показательную функцию: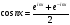 ,
,
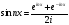 (из формулы Эйлера
(из формулы Эйлера
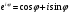 и вытекающего из нее равенства
и вытекающего из нее равенства
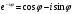 находим, что
находим, что
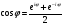 ,
,
 .
Подставив эти выражения в ряд
.
Подставив эти выражения в ряд
 ,
находим:
,
находим:
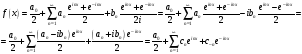
где
обозначено
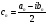 ,
,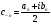 .
.
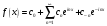 ,
или
,
или
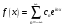 .
.
Коэффициенты
этого ряда можно записать в виде
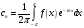
(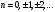 ).
).
Равенство
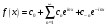 ,
или
,
или
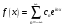 называется комплексной формой ряда
Фурье функции
называется комплексной формой ряда
Фурье функции
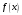 ,
а числа
,
а числа
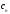 найденные по формуле
найденные по формуле
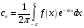 - комплексным коэффициентом ряда Фурье.
- комплексным коэффициентом ряда Фурье.
-
Интеграл Фурье
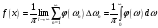 ,
или
,
или
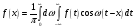 .
.
эта
формула называется формулой Фурье, а
интеграл в правой части формулы –
интегралом Фурье для функции
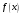 .
.
Данную формулу можно переписать в виде однократного интеграла:
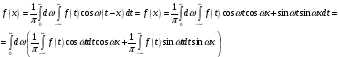
т.е.
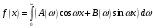 ,
где
,
где
 ,
,
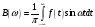 .
.
Если
функция
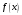 -
четная, то формула
-
четная, то формула
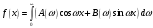 принимает вид
принимает вид
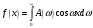 ,
где
,
где
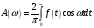 ;
в случае нечетной функции -
;
в случае нечетной функции -
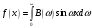 ,
где
,
где
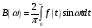 .
.
-
Преобразование Фурье.
Формулу
Фурье
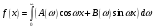 можно представить в симметричной форме
записи, если положить в формулах
можно представить в симметричной форме
записи, если положить в формулах
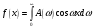 и
и

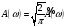 ,
,
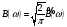 .
В случае четной функции
.
В случае четной функции
 ,
где
,
где
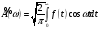 ;
в случае нечетной функции
;
в случае нечетной функции
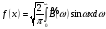 ,
где
,
где
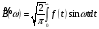 .
.
Функции
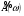 и
и
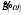 называются соответственно
косинус-преобразованием и
синус-преобразованием Фурье для функции
называются соответственно
косинус-преобразованием и
синус-преобразованием Фурье для функции
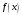 .
.
-
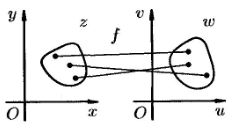
Понятие функции комплексной переменной.
Пусть
даны два множества D
и E,
элементами которых являются комплексные
числа. Числа
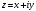 множества D
будем изображать точками комплексной
плоскости
множества D
будем изображать точками комплексной
плоскости
 ,
а числа
,
а числа
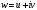 множества E
– точками комплексной плоскости
множества E
– точками комплексной плоскости
 .
.
Если
каждому числу (точке)
 по некоторому правилу поставлено в
соответствие определенное число (точка)
по некоторому правилу поставлено в
соответствие определенное число (точка)
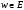 ,
то говорят , что на множестве определена
однозначная функция комплексного
переменного
,
то говорят , что на множестве определена
однозначная функция комплексного
переменного
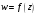 , отображающая множество D
в множестве E.
, отображающая множество D
в множестве E.
Если
каждому
 соответствует несколько значений
соответствует несколько значений
 ,
то функция
,
то функция
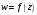 называется многозначной.
называется многозначной.
Множество
D
называется областью определения функции
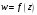 ;
множество E1
всех значений
;
множество E1
всех значений
 ,
которые
,
которые
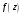 принимает на E,
называется областью значений этой
функции (если же каждая точка множества
E
является значением функции, то E
– область значений функции; в этом
случае функция
принимает на E,
называется областью значений этой
функции (если же каждая точка множества
E
является значением функции, то E
– область значений функции; в этом
случае функция
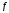 отображает D
на E).
отображает D
на E).
Далее
будем рассматривать такие функции
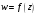 ,
для которых множества D
и E1
являются областями. Областью комплексной
плоскости называется множество точек
плоскости, обладающий свойствами
открытости и связности.
,
для которых множества D
и E1
являются областями. Областью комплексной
плоскости называется множество точек
плоскости, обладающий свойствами
открытости и связности.
Функцию
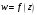 можно записать в виде
можно записать в виде
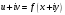 ,
т.е.
,
т.е.
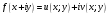 ,
где
,
где
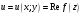 ,
,
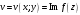 ,
,
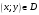 .
.
Функцию
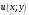 при этом называют действительной частью
функции
при этом называют действительной частью
функции
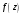 ,
а
,
а
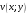 - мнимой.
- мнимой.
Таким образом, задание функции комплексного переменного равносильно заданию двух функций двух действительных переменных.
-
Основные элементарные функции комплексной переменной.
Показательная функция
Показательная
функция
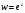 определяется формулой
определяется формулой

Показательная
функция комплексного переменного
обладает специфическим свойством: она
является периодической с мнимым основным
периодом
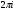 .
.
Действительно,
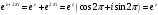 ,
т.е.
,
т.е.
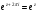
Отметим,
что
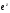 не всегда больше нуля. Например,
не всегда больше нуля. Например,
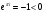
Логарифмическая функция
Эта
функция определяется как функция,
обратная показательной: число
 называется логарифмом числа
называется логарифмом числа
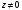 ,
если
,
если
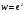 ,
обозначается
,
обозначается
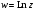 .
Т.к. значения показательной функции
.
Т.к. значения показательной функции
 всегда отличны от нуля, то логарифмическая
функция
всегда отличны от нуля, то логарифмическая
функция
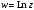 определена на всей плоскости
определена на всей плоскости
 , кроме точки
, кроме точки
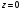 .
.
 ,
т.е.
,
т.е.
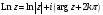 или,
или,
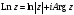 ,
где
,
где
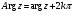 .
.
Формула
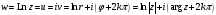 (*) показывает, что функция комплексного
переменного имеет бесчисленное множество
значений, т.е.
(*) показывает, что функция комплексного
переменного имеет бесчисленное множество
значений, т.е.
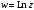 – многозначная функция.
– многозначная функция.
Однозначную
ветвь этой функции можно выделить,
подставив в формулу (*) определенное
значение k.
Положив k=0,
получим однозначную функцию, которую
называют главным значением логарифма
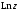 и обозначают символом
и обозначают символом
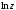 :
:
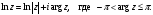
Формулу
(*) можно переписать так
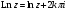 .
.
Из
формулы (*) следует, что логарифмическая
функция
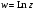 обладает известными свойствами логарифма
действительного переменного:
обладает известными свойствами логарифма
действительного переменного:
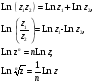
Степенная
функция
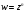 .
.
Если
n
– натуральное число , то степенная
функция определяется равенством
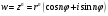 .
Функция
.
Функция
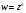 - однозначная.
- однозначная.
Если
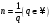 ,
то этом случае
,
то этом случае
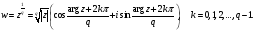
Функция
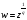 - многозначная.
- многозначная.
Если
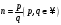 ,
то степенная функция определяется
равенство
,
то степенная функция определяется
равенство
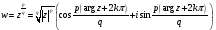
Функция
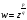 - многозначная.
- многозначная.
Степенная
функция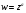 с произвольным комплексным показателем
с произвольным комплексным показателем
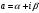 определяется равенством
определяется равенством

Тригонометрическая функция
Тригонометрическая
функции комплексного аргумента
 определяются равенствами
определяются равенствами
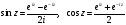 ,
,
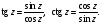 При действительных
При действительных
 эти определения приводят к тригонометрическим
функциям действительного переменного.
Так, при
эти определения приводят к тригонометрическим
функциям действительного переменного.
Так, при

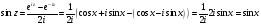 .
.
Гиперболические функции Эти функции определяются равенствами
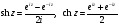 ,
,
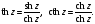
Заменяя
в указанных функциях
 на
на
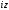 ,
получим:
,
получим:
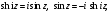
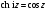 (
(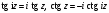 ).
).
Обратные тригонометрические и гиперболические функции
Число
w
называется арксинусом числа z,
если
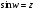 и обозначается
и обозначается
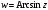 .
.