ЛР_ТВ_часть3

где [ϕ]T – матрица, транспонированная по отношению к [ϕ].

Так как при одномерном обратном преобразовании в общем случае также

выполняется соотношение
[ f ] = [ϕ] -1 [g] = [ϕ]-1 [ϕ][ f ],	(10.7)
при ортонормальном преобразовании обратная матрица определяется
транспонированной матрицей
[ϕ]-1 = [ϕ]T ,	(10.8)
и одновременно выполняется условие
[ϕ]-1[ϕ]T = Е,	(10.9)

где Е – единичная матрица.

Если транспонированная матрица удовлетворяет, кроме того, условию симметрии по отношению к главной диагонали, то дополнительно выполняется

условие

[ϕ]-1 = [ϕ]T = [ϕ],

(10.10)

в соответствии с которым ядро преобразования одинаково для прямого и об- ратного преобразования.

Ортонормальному одномерному преобразованию присущи следующие свойства:

–сумма произведений элементов любой строки (столбца) на соответст- вующие элементы другой строки (столбца) транспонированной матрицы равна нулю;

–сумма квадратов элементов любой строки (столбца) соответствует энер- гии основного (инвертированного) сигнала и равна единице;

–обратная матрица преобразования получается в результате транспони- рования исходной матрицы.

Аналогично и двумерное прямое преобразование будет определяться формулой

N −1 N −1
g(u,v) = å åϕu,v (x, y) f (x, y) ,	(10.11)

x=0 y=0

в результате решения которой получим N 2 трансформант (спектральных коэф- фициентов), определяющих амплитуды набора двумерных ортогональных

31

функций. В общем случае трансформанта определяется (u,v)-й ортогональной функциейϕu,v (x, y) и величинами отсчетов f (x, y) на плоскости. Исходная двумерная функция f (x, y) с использованием трансформант может быть пред-

ставлена системой двумерных ортогональных функций

N −1	N −1
f (x, y) = å å g(l,r)jl,r (x, y) .		(10.12)
l=0	r=0

В соответствии с этой формулой осуществляется обратное преобразова-

ние.

Запись матрицы трансформант и следовательно, формулы преобразова- ния можно упростить, если двумерную систему ортогональных функций пред- ставить как произведение одномерных ортогональных функций, например век-

тора-столбца ϕuT и вектора-строки ϕv :

ϕu,v = ϕuT × ϕv .

(10.13)

Формула одновременно отражает способ определения базисных изобра- жений двумерного преобразования с разделяемым ядром. Для элементов мат- рицы трансформант g(u,v) в матричной форме выполняется соотношение

g(u, v) = [jv ][ f ] [ju ]T ,	(10.14)
или в общем случае для матрицы трансформант g(u,v)
[g] = [j][ f ][j]T .	(10.15)

В соответствии с приведенным выражением двумерное прямое преобра-

зование можно представить как две последовательно выполняемые одномерные операции. Первая операция заключается в умножении сигнальной матрицы [ f ] слева на вектор-строку матрицы [ϕv ] и соответствует одномерному преобразо- ванию столбцов матрицы [ f ] .

Дискретно-косинусное преобразование

Недостатком широко использующегося в задачах цифровой обработки сигналов дискретного преобразования Фурье (ДПФ) с точки зрения кодирова- ния с преобразованием заключается в том, что трансформанты, общее количе- ство которых составляет 2N, а период равен T = N · T, носят комплексный ха- рактер. Учитывая состав трансформант, целесообразнее осуществлять такое

32

преобразование, в котором используется только реальная или мнимая часть яд- ра преобразования, т.е. только члены cos или sin. Однако в этом случае необхо- димо обеспечить полноту ортогональной системы преобразования.

Если перейти от общего ДПФ к более специфическому ДКП, основанно- му на базисе ортогональных косинусных составляющих, то выбором соответст- вующего интервала Т необходимо добиться того, чтобы множество ортогональ- ных функций образовало полную систему. В качестве ортогональных функций нельзя выбирать обычные косинусные функции cos(kΩ0t), т. к. это связано с использованием функций sin(kΩ0t) . Удовлетворить условие ортогональности

проще всего выбором ортогональных составляющих вида cos(kTπ) , что в более

полной форме можно записать как

jk

= cos

2n + 1

kp,

k, nÎ{0,K, N -1}.

(10.16)

2N

Так как для ортогональной системы выполняется соотношение

N −1

æ

2n +1

ö

æ

2n +1

ö

ì0

для k = l,

åcosç

kp÷

× sinç

lp÷

= í

для k ¹ l,

(10.17)

2N

2N

n=0

è

ø

è

ø

îKk,l

то ортогональная система в соответствии с выражением (10.16) образует пол- ную систему и ее можно использовать в качестве основы ДКП.

Соответствующие постоянные нормирования для образования ортого- нальной системы находятся из условия ортогональности на интервале N:

N −1

æ 2n +1

ö

æ 2n +1

ö

ìN

для k = l = 0,

ï

åcosç

kp÷

× cosç

lp÷

= íN / 2

для k = l ¹ 0,

(10.18)

2N

2N

n=0

è

ø

è

ø

ï

для k ¹ l.

î0

Если ввести константу нормирования в выражения как для прямого, так и для обратного преобразований, то при одномерной полной системе ортогональ-

ных функций ДКП получим

é

1

2n +1

ù

k Î{1, 2,K, N -1},

2

(10.19)

jk = ê

,

cos

kpú,

n Î{0, 1,K, N -1}.

N

2N

N

ë

û

Собственно ядро преобразования при переходе от ДПФ к ДКП определя-

ется как

33

		2n +1		ì	é	p	ù	é	p	ùü
	cos			kp = Reíexpê- j			kú	× expê- j		knúý.	(10.20)
		2N				2N			2N
				î	ë		û	ë		ûþ

С учетом этого после преобразований получаем выражение для прямого преобразования

	1					N −1
C(0) =						å f (n),
			N n=0						(10.21)
						N −1	2n +1
	2
C(k) =						å f (n)cos			kp, k Î{1, 2,K, N -1}.
							2N
			N n=0

Упрощенная стандартная формула обратного одномерного ДКП имеет

вид

1

2

N −1

2n +1

f (n) =

C(0)

+

åC(k)cos

2N

kp.

(10.22)

N

N k 1

=

Приведенные выше формулы для одномерного ДКП можно путем фор- мального преобразования привести к замкнутому виду. Тогда прямое преобра-

зование будет определяться выражением

			2			N −1
	C(k) =					c(k) å f (n)cos 2n +1kp, k Î{0,1,K, N -1},		(10.23)
				N
						n=0	2N
	а обратное преобразование –
				N −1			2n +1kp, nÎ{0,1,K, N -1},	(10.24)
	f (n) = åc(k)C(k)cos
				k=0			2N
	ì		1			для k = 0,
	ï
	где c(k) = í		2
	ï					для k Î{1, 2,K, N -1}.
	î1
	Матричная форма записи прямого ДКП имеет вид
	[C(k)]= [ϕ(k,n)][f (n)],							(10.25)

где [C(k)] – матрица-столбец спектральных коэффициентов ДКП размером

(1 × N);

[ϕ(k,n)] – матрица дискретного множества ортогональных функций ДКП размером (N × N) в соответствии с (10.19);

[f (n)] – матрица-столбец дискретных значений (отсчетов) сигнала.

34

Соответствующее обратное одномерное преобразование в матричной форме записи представляется в виде

[f (n)]= [j(k,n)]−1 [C(k)],

(10.26)

А поскольку условие симметричности матрицы преобразования по отно- шению к ее главной диагонали не выполняется, то

[j(k,n)]−1 = [j(k,n)]T ,

(10.27)

и соответственно

[f (n)]= [j(k,n)]T [C(k)],

k,n Î{0,1,K, N -1}.

(10.28)

Для преобразования двумерных фрагментов используется двумерное пре- образование, ядро которого (без учета константы нормирования) имеет вид

jˆ (k, n, l, m) = cos	2n +1	kp × cos	2m +1	lp,		k, nÎ{0,1,K, N -1},	(10.29)
						l, mÎ{0,1,K, N -1}.
	2N		2M
Таким образом, прямое ДКП двумерного фрагмента форматом (N × M)
запишется как
[C(k,l)]= [j(k,n)][f (n,m)][j(l,m)]T ,							(10.30)

где [C(k,l)] – матрица спектральных коэффициентов ДКП размером (N × М); [f (n,m)] – сигнальная матрица размером (N × М);

[ϕ(k,n)] – квадратная матрица функций ДКП размером (N × N):

é

1

ù

ê

ú

k Î{1, 2,K, N -1},

2

j(k,n) =

2

ê

2n +1

ú,

nÎ{0,1,K, N -1}.

(10.31)

N ê

ú

êcos

2N

kpú

ë

û

[j(l,m)]T – квадратная матрица функций ДКП размером (М × М), транспо-

нированная по отношению к матрице

é

1

ù

ê

ú

l Î{1, 2,K, N -1},

j(l,m) =

2

2

ê

2m +1

ú,

mÎ{0,1,K, N -1}.

(10.32)

N ê

ú

êcos

lpú

2M

ë

û

35

Соответствующая матричная форма записи двумерного обратного ДКП имеет вид

[f (n,m)]= [ϕ(k,n)]T [C(k,l)][ϕ(l,m)].

(10.33)

Если одномерное преобразование последовательности N отсчетов сигнала f (n) , n {0, 1,K, N −1} во времени алгебраически интерпретировать как пре- образование координат векторов в N-мерном метрическом пространстве, то ис- ходя из основной формулы преобразования с ядром [CN ]

[c]= [CN ][f ],

(10.34)

где [c], [f ] – матрицы-столбцы векторов c спектра и f исходного сигнала,

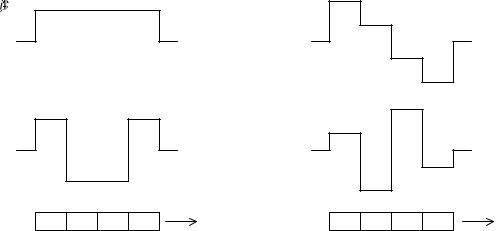
векторам базиса пространства сигналов ставятся в соответствие векторы в спектральной области. В связи с ортогональностью ДКП также характеризуется тем, что векторы преобразования, за исключением первого, равны нулю. Коор- динаты векторов преобразования представляют собой элементы соответствую- щей строки матрицы преобразования [CN ].

Графическая иллюстрация координат векторов преобразования C j (i), j, i {0, 1,K, N −1}, для N = 4 приведена на рисунке 10.2.

Рисунок 10.2 – Координаты векторов одномерного ДКП для N = 4

Если двумерное преобразование последовательности N 2 элементов изо-

бражения f (x, y), x, y {0, 1,K, N −1}, алгебраически	интерпретировать как
преобразование координат векторов в N 2-мерном пространстве, то в соответст-
вии с обобщенной формулой
[c]= [N Cu,v (x, y)][f ],	(10.35)
36

где [c], [f ] – спектральная и сигнальная матрицы размером (N × N),

[N Cu,v (x, y)], x, y, u, v {0, 1,K, N −1} – матрица преобразования размером

(N 2× N 2),
отдельным векторам базиса пространства сигналов	f (x, y) = 1,

x, y {0, 1,K, N −1}, ставятся в соответствие векторы базисы в спектральной области. Координатам векторов преобразования, число которых составляет N 2, в этом случае непосредственно соответствуют отдельные матрицы N Cu,v (x, y) ,

принадлежащие множеству матриц преобразования [N Cu,v (x, y)] для u, v {0, 1,K, N −1}. Их графические представления зависят от типа ядра пре- образования [CN ] и для порядка преобразования N = 4 приведены на рисунке 10.3. Представленные двумерные функции являются так называемыми базис- ными изображениями ДКП и образованы двумерной дискретной системой ор- тогональных функций ДКП. Для разделяемого ядра преобразования они нахо- дятся как результат перемножения вектора-столбца cuT и вектора-строки cv со-

ответствующей матрицы преобразования

cu,v = cuT × cv

(10.36)

Множество двумерных базисных изображений ДКП представляет собой множество двумерных функций, по которым раскладывается данный фрагмент изображения f (x, y).

φ00

φ01

φ02

φ03

φ10

φ11

φ12

φ13

φ20

φ21

φ22

φ23

φ30

φ31

φ32

φ33

Рисунок 10.3 – Графическое представление базисных изображений двумерного ДКП 4×4

37

10.3 Выполнение работы

10.3.1 Исследование влияния параметров ДИКМ на качество воспроизво-

димого изображения

10.3.1.1Открыть любой файл bmp-формата из папки «Images» пакета

VCDemo.

10.3.1.2На панели управления включить режим исследования ДИКМ

(кнопка «DPCM»).

10.3.1.3В появившемся окне «DPCM» в подменю «Model» выбрать мо-

дель предсказания («Set the prediction model»).

Примечание: используются либо одномерная (1-я), либо двумерные (2-я

–4-я) модели предсказания.

10.3.1.4Изменяя разрядность квантования («DPCM bitrate»), проследить за изменением субъективного качества изображений, а также отношения сиг-

нал/шум («signal-to-noise ratio»).

10.3.1.5Повторить п. 10.3.1.4 для различных моделей предсказания.

10.3.1.6Повторить п.п. 10.3.1.4 – 10.3.1.5 при различной вероятности ошибки. Для этого включить режим имитации ошибок в канале «Simulate channel errors», и, устанавливая различную вероятность ошибок, проследить их влияние на качество изображения и отношение сигнал/шум. Результаты п.п. 10.3.1.4 – 10.3.1.6 занести в сводную таблицу 10.1. Выполнить для нескольких, различающихся по сюжету изображений. Построить графические зависимости СКИ (m) для различных моделей предсказания (в одной системе координат), ОСШ (КОШ) при различных разрядностях квантования.

Таблица 10.1

Тип	Краткая характери-	Модель	Разряд-	ОСШ,	Субъективное качество изображения						Число
(назва-	стика (сюжет, осо-	пред-	ность	дБ		(СКИ) по 5-балльной шкале					бит на
ние)	бенности, размер	сказа-	кванто-								отсчет
изобра-	преобладающих	ния	вания m								при ис-
жения	деталей – мелкие,		(число								пользо-
	средние, крупные –		бит на		Без		0.005	0.001	0.0005	0.0001	вании
	в горизонтальном и		отсчет)		оши-						кода
	вертикальном на-				бок						пере-
	правлении)										менной
											длины
			1
			2
			4
			6

38

10.3.2 Исследование влияния параметров ДКП на качество преобразо-

ванного изображения

10.3.2.1Открыть любой файл bmp-формата из папки «Images» пакета

VCDemo.

10.3.2.2На панели управления включить режим исследования ДКП (кноп-

ка «DСТ»).

10.3.2.3В появившемся окне «DСТ» в подменю «Size» выбрать размер блока ДКП («Set transform size»).

10.3.2.4Устанавливая различное количество бит/отсчет (подменю «bitrate») проследить за изменением субъективного качества преобразованного изображения и отношения сигнал/шум. Проделать этот эксперимент для раз- личных моделей предсказания (при условии выбора ДИКМ для квантования коэффициентов ДКП).

10.3.2.5Повторить п. 10.3.2.4 для разных размеров блока преобразования. Результаты п.п. 10.3.2.4, 10.3.2.5 свести в таблицу 10.2. Повторить для несколь- ких изображений – испытательных и реальных.

Таблица 10.2

Тип (на-	Краткая характеристика (сюжет, особен-	Размер	Число	Субъективное
звание)	ности, размер преобладающих деталей –	блока*	бит/	качество изобра-
изобра-	мелкие, средние, крупные – в горизон-		отсчет	жения по 5-
жения	тальном и вертикальном направлении).			балльной шкале
			0,25
			0,5
		2×2	1
			2
			3
			4
		4×4
		8×8
		16×16

* размер блока ДКП должен являться делителем числа отсчетов преобра- зуемого изображения.

39

10.4 Содержание отчета

1 Титульный лист.

2Цель работы.

3Результаты исследований по п. 10.3.

4Вывод.

10.5 Вопросы для самопроверки

1При какой разрядности квантования преобразованное изображение зри- тельно неотличимо от оригинала?

2Как влияет модель предсказания на качество изображения? В чем это выражается?

3Какого коэффициента сжатия позволяет достичь ДИКМ?

4Как отражаются на изображении ошибки в канале связи при использо- вании ДИКМ? Зависит ли восприятие помех, вызываемых ошибками в канале связи, от модели предсказания?

5Поясните различное влияние на изображение помех от ошибок в канале связи при ИКМ и ДИКМ.

6Рассчитайте максимальное количество пораженных отсчетов изобра- жения размером 256×256 при вероятности ошибки в канале связи 10-3 при: а) ИКМ с разрядностью 8 бит/отсчет; б) ДИКМ с разрядностью 2 бит/отсчет.

7При какой модели предсказания заметность помех от ошибок в канале связи выше и почему?

8При какой разрядности квантования (минимальной или максимальной) влияние ошибок в канале связи на качество изображения больше?

9Для какого типа изображений (с преобладающими мелкими либо пре- обладающими крупными деталями) использование ДИКМ более эффективно?

10Почему при использовании ДИКМ помеха, вызываемая ошибками в канале связи, на различных изображениях заметна по-разному?

11Поясните причину возникновения муар-эффекта при ДИКМ.

12Поясните, как и почему изменяется заметность муар-эффекта при из- менении масштаба изображения? При каких условиях муар-эффект минимален?

13При какой разрядности ДИКМ (минимальной, средней или макси- мальной) может быть достигнут наибольший выигрыш от использования эн- тропийного кодирования?

40