641132TВ - -TБ TА3_13.01.2015

Задание 1

1. Для данного интервального вариационного ряда построить:

а) гистограмму частот;

б) кумуляту частот;

в) эмпирическую функцию распределения.

2. Построить дискретный вариационный ряд, взяв в качестве вариант середины интервалов.

3. Найти выборочные характеристики положения и отметить их на графике, построенном в п. 1.а):

а) среднюю арифметическую ;

б) медиану Ме и моду Мо.

4. Найти характеристики рассеяния:

а) выборочную дисперсию ;

б) исправленную выборочную дисперсию ;

в) среднее квадратическое отклонение и «исправленное» среднее квадратическое отклонение ;

г) размах варьирования R и коэффициент вариации .

Вариант		1	2	3	4	5	6
22	X	(0;1]	(1;2]	(2;3]	(3;4]	(4;5]	(5;6]
	ni	66	19	7	5	2	1

Решение.

1. Построим:

а) гистограмму частот;

б) кумуляту частот:

в) эмпирическую функцию распределения:

2. Построим дискретный вариационный ряд, взяв в качестве вариант середины интервалов:

xi	ni
0,5	66
1,5	19
2,5	7
3,5	5
4,5	2
5,5	1
Итого	100

3. Найдем выборочные характеристики положения:

а) среднюю арифметическую ;

;

б) медиану Ме и моду Мо.

Мода определяется по формуле:

нижняя граница модального интервала;

h – интервал группирования, у нас равен 1;

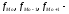частоты модального, передмодального и послемодального интервалов.

Медиану определим по формуле (медианный интервал – такой, в котором суммарная частота начинает превышать половину суммы всех частот):

нижняя граница медианного интервала;

суммарная частота передмедианного интервала;

частота медианного интервала.

4. Найдем характеристики рассеяния:

а) выборочную дисперсию ;

б) исправленную выборочную дисперсию ;

_{в) среднее} квадратическое отклонение _{= ;}

«исправленное» среднее квадратическое отклонение _{= 1,63};

г) размах варьирования R = 6 – 0= 6,0;

коэффициент вариации ₌ 1,0573/ 1,11*100 = 95,25%.

Задание 2

По данным задания 1 используя критерий при уровне значимости , проверить гипотезу о том, что случайная величина X распределена по нормальному закону (нечётные варианты) или по экспоненциальному закону (чётные варианты).

Решение.

Вид распределения:

Параметр в данном случае равен:

λ = 1/ = 1/1,11 = 0,901.

Получаем:

Проверка проводится следующим образом.

теоретические частоты вычисляются по формуле

                            

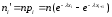
Затем сравниваются наблюдаемое и критическое значение критерия Пирсона с учетом того, что число степеней свободы k = s – 2.

Затем рассчитываем фактическое значение критерия Пирсона:

Сравниваем с критическим значением.

Вспомогательные значения:

xi	xi+1	ni			pi	ni'	(ni-ni')^2/ni'
0	1	66	1,00	0,41	0,59	59,384	0,737
1	2	19	0,41	0,16	0,24	24,119	1,087
2	3	7	0,16	0,07	0,10	9,796	0,798
3	4	5	0,07	0,03	0,04	3,979	0,262
4	5	2	0,03	0,01	0,02	1,616	0,091
5	6	1	0,01	0,00	0,01	0,656	0,180
Итого							3,155

Фактическое значение критерия равно

Критическое значение при к = 6 – 2 = 4 степенях свободы и уровне значимости 0,95 – 9,5. Поскольку это значение больше фактического, то гипотезу о показательном распределении следует принять.

Задание 3

1. Построить уравнение регрессии , используя формулы:

2. Оценить значимость уравнения регрессии по F-критерию Фишера-Снедекора:

наблюдаемое значение критерия ,

сравним с табличным значением

при уровне значимости и степенях свободы , п – число наблюдений, т – число оцениваемых параметров (b₀, b₁);

уравнение регрессии значимо, если ;

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Средние квадраты
Регрессия
Остаточная
Общая

3. Вычислить коэффициент корреляции r:

4. Оценить значимость коэффициента корреляции по t-критерию Стьюдента:

наблюдаемое значение критерия:

,

сравним с табличным значением

при уровне значимости и степенях свободы ;

коэффициент корреляции значим, если .

Варианты

	22
1	-7	1
2	-5	3
3	-4	7
4	-3	5
5	0	6
6	2	3
7	4	-3
8	6	-1
9	8	2
10	10	5

Решение.

1. Построим уравнение регрессии ,

Вспомогательные данные:

	x	y	x^2	y^2	x*y
	-7	1	49	1	-7
	-5	3	25	9	-15
	-4	7	16	49	-28
	-3	5	9	25	-15
	0	6	0	36	0
	2	3	4	9	6
	4	-3	16	9	-12
	6	-1	36	1	-6
	8	2	64	4	16
	10	5	100	25	50
Сумма	11	28	319	168	-11
Среднее	1,1	2,8	31,9	16,8	-1,1

Рассчитываем средние так:

Используем формулы:

Уравнение:

2. Оценим значимость уравнения регрессии по F-критерию Фишера-Снедекора.

Вспомогательные данные:

y	yteor	(y-yteor)^2	(y-ysr)^2
1	3,9032	8,42857	3,24
3	3,6308	0,397909	0,04
7	3,4946	12,28783	17,64
5	3,3584	2,694851	4,84
6	2,9498	9,30372	10,24
3	2,6774	0,104071	0,04
-3	2,405	29,21403	33,64
-1	2,1326	9,813183	14,44
2	1,8602	0,019544	0,64
5	1,5878	11,64311	4,84
Сумма		83,90681	89,6

Наблюдаемое значение критерия

,

сравним с табличным значением при уровне значимости и степенях свободы , п – число наблюдений, т – число оцениваемых параметров (b₀, b₁), оно равно 11,26;

уравнение регрессии значимо, если

В нашем случае это не выполняется.

3. Вычислим коэффициент корреляции r:

Вспомогательные данные:

Получаем:

4. Оценить значимость коэффициента корреляции по t-критерию Стьюдента:

наблюдаемое значение критерия:

,

сравним с табличным значением _, при уровне значимости и степенях свободы оно равно 2,37. Коэффициент корреляции значим, если .

В нашем случае это не выполнено.

Литература.

1. Гмурман В. Е. Теория вероятностей и математическая статис­тика. — М.: Высш. шк., 1999.

2. Горбань С. Ф., Снижко Н. В. Теория вероятностей и математи­ческая статистика. — К.: МАУП, 1999.

3. Гурский Е. М. Теория вероятностей с элементами математичес­кой статистики. — М.: Высш. шк., 1971.

11