konspekt_lektsy_biblioteka_2

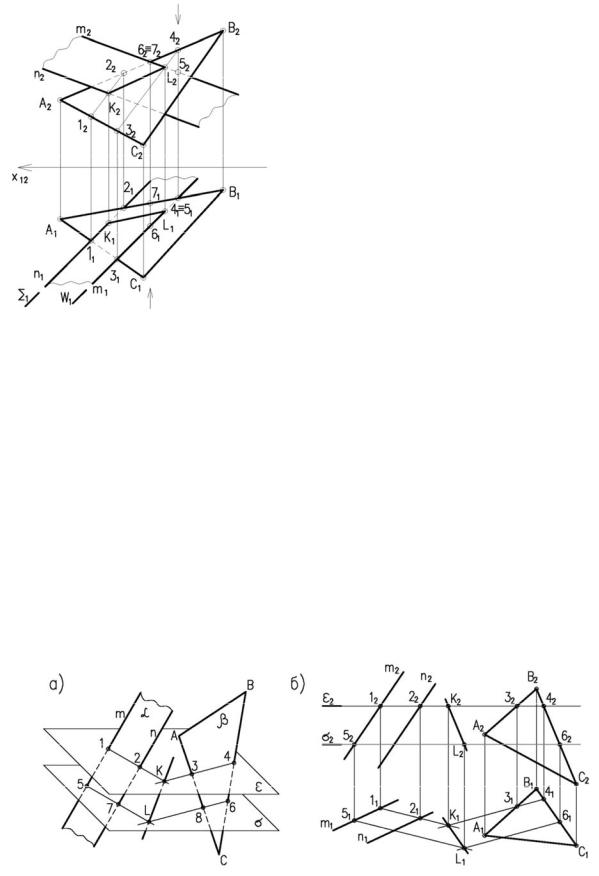
Пересечение двух плоскостей

Две плоскости пересекаются по прямой линии, поэтому для её построения достаточно найти две точки одновременно принадлежащие двум плоскостям.

Рассмотрим несколько случаев построения линии пересечения двух плоскостей.

1-й случай – пластины непрозрачные зада-

ны с нахлёстом (рисунок 2.10).

Задача сводится к нахождению точек пере-

сечения прямых m и n с плоскостью ά (∆ АВС).

Соединив точки пересечения К и М получим ли-

нию пересечения плоскости ά (∆ АВС) с плоско-

стью β (m//n). Видимость определяется по конку-

рирующим точкам.

Рисунок 2.10 2-й случай – плоскости заданы на некотором расстоянии, что не дает возможность

определить линии пересечения двух плоскостей первым способом. В этом случае использу-

ется метод плоскостей-посредников.

Алгоритм решения задачи (рисунок 2.11):

1.Заданные плоскости ά и β рассекаем вспомогательной плоскостью посредником ε;

2.Определяем линию пересечения 1-2 плоскости ά с плоскостью σ и линию пересе-

чения 3-4 плоскости β с плоскостью ε;

3.Определяем точку К – точку пересечения линий 1-2 и 3-4, принадлежащую плос-

костям ά и β;

4.Аналогичным образом находим точку L с помощью плоскости посредника σ;

5.Соединив две точки К и М, получим линию пересечения двух плоскостей ά и β.

Видимость при этом не определяется.

Рисунок 2.11

20

3-й случай – пересекающиеся плоскости об-

щего положения заданы следами пересекающимися в пределах чертежа (рисунок 2.12).

В данном случае в качестве плоскостей-

посредников могут быть использованы плоскость

проекций П1 и П2.

Рисунок 2.12

Пересечение многогранника проецирующей плоскостью

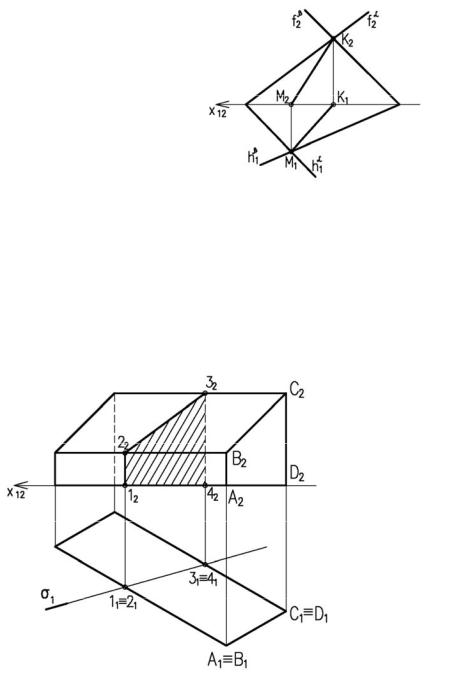
Так как секущая плоскость горизонтально-проецирующая, то фронтальную проекцию сечения можно построить, определив точку пересечения каждого ребра с плоскостью σ (ри-

сунок 2.13)

Рисунок 2.13

21

Лекция 3. Решение метрических задач

∙Метрические задачи.

∙Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольного треугольника.

∙Решение метрических задач методами преобразования проекций

-Положения геометрических образов, при которых расстояния и углы не искажаются на плоскостях проекций.

-Четыре основные задачи преобразования проекций.

-Решение 1-ой и 2-ой задачи преобразования проекций методом вращения,

плоскопараллельного перемещения и замены плоскостей проекций.

-Решение 3-ой и 4-ой задачи преобразования проекций методом плоскопа-

раллельного перемещения и замены плоскостей проекций.

Метрические задачи

К метрическим задачам относятся задачи на определение натуральной величины от-

резков, расстояний углов, площадей плоских фигур.

Определение натуральной величины отрезка и углов наклона к плоскостям

проекций методом прямоугольного треугольника

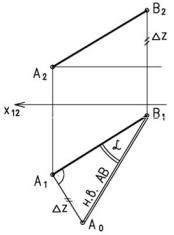
Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым – разность расстояний концов отрез-

ка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и ка-

тетом проекций является углом наклона отрезка к той плоскости,

на которой ведется построение. На рисунке 3.1 построение нату-

ральной величины выполнено на горизонтальной проекции. По-

этому одним катетом прямоугольного треугольника, является го-

ризонтальная проекция А1В1, второй равен разности координат z

точек А и В. Угол α между н.в. (натуральной величиной) и катетом проекций равен углу наклона отрезка АВ к плоскости проекций П1.

Если необходимо определить угол наклона отрезка АВ к

плоскости П2, то построение прямоугольного треугольника ведет-

Рисунок 3.1

ся на фронтальной проекции.

22

Решение метрических задач методами преобразования проекций

Положения геометрических образов, при которых расстояния и углы не искажаются на плоскостях проекций

Метрические характеристики объектов на чертежах не искажаются, если геометриче-

ские образы занимают частное положение относительно плоскостей проекций.

Приведем некоторые из них.

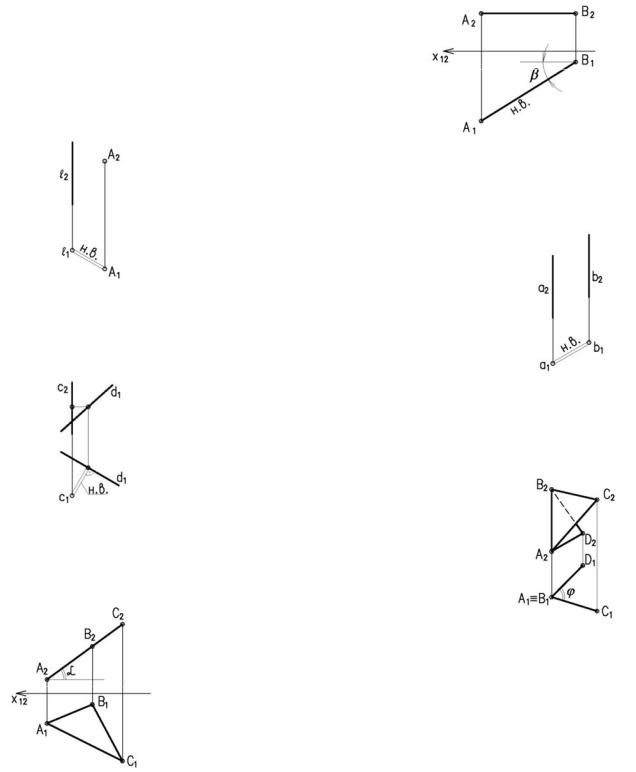
1.Прямая проецируется в натуральную величи-

ну, если она параллельна плоскости проекций (рисунок 3.2).

β– угол наклона к плоскости П2

Рисунок 3.2

2.Расстояние от точки до прямой проецируется в нату-

ральную величину, если прямая проецирующая (рисунок 3.3).

Рисунок 3.3 3. Расстояние между параллельными прямыми проецируется в

натуральную величину, если прямые проецирующие (рисунок 3.4).

Рисунок 3.4

4.Расстояние между скрещивающимися прямыми про-

ецируется в натуральную величину, если одна из прямых проециру-

ющая (рисунок 3.5).

Рисунок 3.5

5.Угол между плоскостями (двугранный угол) проецируется

внатуральную величину, если ребро угла проецирующее (рисунок 3.6).

Рисунок 3.6 6. Угол наклона плоскости к плоскости проекций

проецируется в натуральную величину, если плоскость проеци-

рующая (рисунок 3.7)

Рисунок 3.7

23

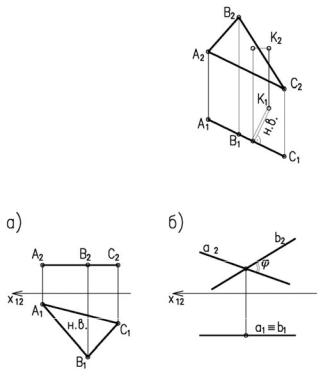
7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)

Рисунок 3.8

8.Любая плоская фигура про-

ецируется в натуральную величину, если она параллельна плоскости проекций (рису-

нок 3.9а,б)

Рисунок 3.9

Таким образом, для решения метрических задач целесообразно данный объект приве-

сти в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи.

Для такого перехода и служат способы преобразования проекций.

Существует несколько способов преобразования проекций: способ вращения во-

круг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемеще-

ния, способ замены плоскостей проекций и др.

Четыре основных задачи преобразования проекций.

Этими способами решаются четыре основные задачи:

Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразо-

вание).

Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразо-

вания)

Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобра-

зование)

Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобра-

зования)

24

Решение 1-ой и 2-ой задачи преобразования проекций методом вращения, пло-

скопараллельного перемещения и замены плоскостей проекций

Способ вращения

Способ вращения заключается в том, что гео-

метрические образы вращаются вокруг осей перпен-

дикулярных плоскостям проекций до занятия ими ка-

кого-либо частного положения относительно плоско-

стей проекций. При этом одна проекция точки пере-

мещается по окружности, вторая – по прямой парал-

лельной оси проекций.

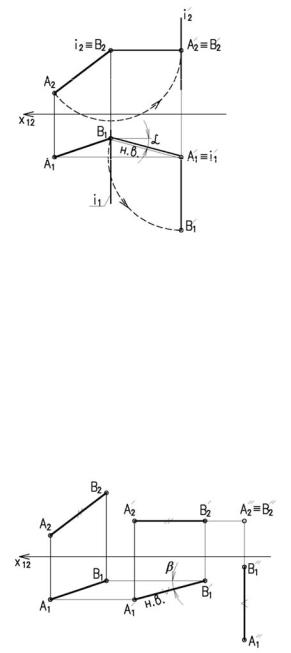
На рисунке 3.10 вокруг оси i ┴ П2 вращаем от-

Рисунок 3.10 резок АВ до положения параллельного плоскости П1 (1

задача). Далее вращением вокруг оси i' ┴ П1, полученный отрезок до положения перпенди-

кулярного плоскости П2 (А1'В1' ┴Х12). На П2 отрезок спроецируется в точку (А2'≡В2').

Способ плоско-параллельного перемещения

Способ плоскопараллельного перемещения является разновидностью способа враще-

ния (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать пу-

тем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного

положения.

На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонталь-

ное. При этом А2'В2' должно быть равно по ве-

личина А2В2. А1'В1' находим в пересечении вер-

тикальных линий связи и линий А1А1', В1В1' па-

раллельных оси х12 (1 задача). Далее отрезок

А1'В1' перемещаем до положения перпендикулярного оси

Рисунок 3.11

х12. При этом А1''В1''= А1'В1'. На фронтальной проекции отрезок спроецируется в точку (А2''≡В2'') (2 задача).

Способ замены плоскостей проекций

Сущность способа замены плоскостей проекций заключается в том, что старая систе-

ма плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций

25

и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси.

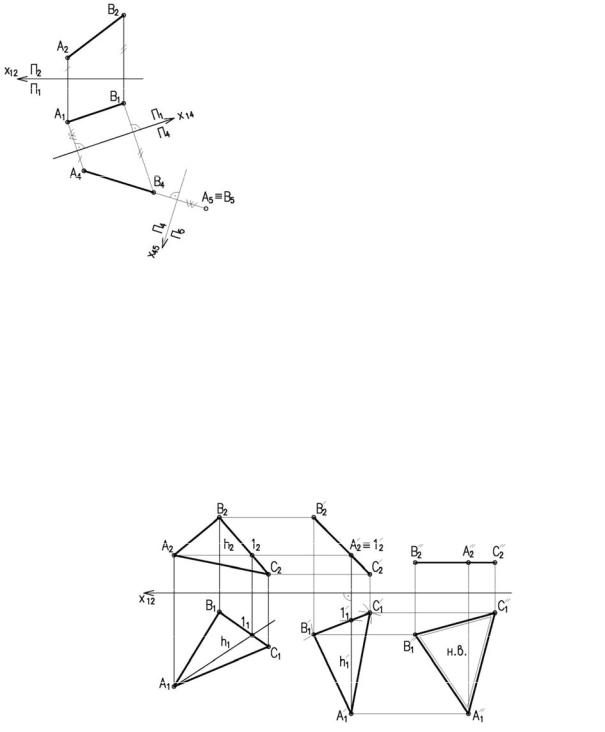
	На рисунке 3.12 произведена первая замена –
	плоскость П2 заменена на новую фронтальную плос-
	кость П4 параллельную прямой АВ. При этом новая ось
	х14 проводится параллельно проекции А1В1. Линии связи
	проводятся перпендикулярно оси х14 и на них от х14 от-
	кладываются координаты z точек А и В (1 задача).
	Далее прямую АВ преобразуем в проецирующую.
	Для этого проводим новую ось х54 перпендикулярно
	проекции А4В4. Т.к. А1В1 параллельна оси х14, расстояние
	до проекций А5 и В5 будет одинаковое и прямая спро-
Рисунок 3.12	ецируется в точку (А5≡В5). (2 задача)

Решение 3-ой и 4-ой задачи преобразования проекций методом плоскопарал-

лельного перемещения и замены плоскостей проекций

Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плос-

костей проекций.

Способ плоскопараллельного перемещения

Рисунок 3.13

Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плос-

кости проекций. Поэтому на рисунке 3.13 проведена горизонталь h(h1,h2). Далее h1 распола-

гаем перпендикулярно оси х12. Откладываем на ней отрезок А111 и циркулем строим тре-

угольник А1'В1'С1' равный по величине А1В1С1. На фронтальной проекции треугольник спро-

ецируется в линию (3 задача).

26

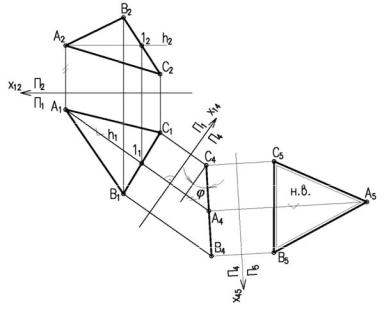
Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию А2'В2'С2' расположить параллельно оси х12, при этом на горизонтальной проекции треугольник спроецируется в натуральную величину (4-я задача)

Способ замены плоскостей проекций

Рисунок 3.13

При решении задачи методом замены (рисунок 3.14) новую ось х14

проводим перпендикулярно горизон-

тали h1, тогда на новую фронталь-

ную плоскость П4, треугольник спроецируется в линию, т.е. станет перпендикулярным (3-я задача).

Чтобы плоскость перевести в поло-

жение плоскости уровня, необходи-

мо новую ось х54 провести парал-

лельно плоскости А4В4С4. На новую плоскость П5 треугольник спроеци-

руется в натуральную величину.

Для того, чтобы методами преобразования решить любую метрическую задачу, необ-

ходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.

27

Лекция 4. Тени в ортогональных проекциях

Метод следа луча, метод выноса

∙Общие положения.

∙Тень точки – способ следа луча, способ выноса.

∙Тень прямой общего положения.

∙Тени прямых частного положения.

∙Тени плоских фигур.

∙Тень окружности.

∙Тени поверхностей. Понятие собственной и падающей тени.

Общие положения

Проекционные чертежи архитектурных объектов выполненные в одних линиях, не дают достаточно полного представления о запроектированном объекте.

Для придания объемности и наглядности ортогональным чертежам зданий и сооруже-

ний выполняется построение теней.

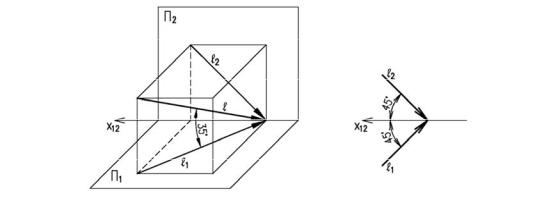
Тени строятся от естественного освещения, т.е. солнца. Так как солнце практически бесконечно удаленная точка, то лучи принимаются параллельными. За направление лучей принимается диагональ куба грани которого совпадают с плоскостями проекций, а её проек-

ции являются диагоналями граней куба, т.е. квадратов (см. рисунок 4.1). Истинный угол наклона будет равен 35°, а проекции лучей располагаются под углом 45° к оси (см. рисунок

4.1).

Рисунок 4.1

Тень точки – способ следа луча, способ выноса

Тенью точки на плоскости является точка пересечения светового луча, прове-

денного через данную точку, с плоскостью. Если тень точки падает на плоскость проек-

28

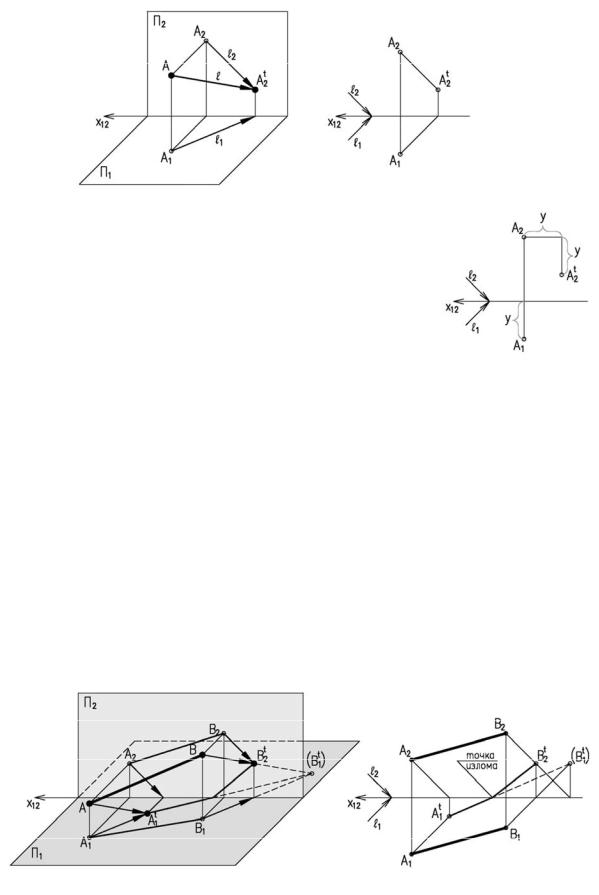
ций, то для её построения используется способ следа луча. Т.е. через проекции точки прово-

дим проекции лучей и строим след. На рисунке 4.2 след луча фронтальный, следовательно тень падает на фронтальную плоскость – А 2t.

Рисунок 4.2
Кроме этого может быть использован метод выноса. Особен-
но важен этот метод при построении теней на фасадах зданий.
Вынос – это расстояние от точки до фронтальной плоскости
или плоскости фасада, если тень строится на фасаде. На рисунке 4.3
y – это вынос.	Рисунок 4.3
Тень прямой общего положения

Тенью прямой на плоскость является линия пересечения лучевой плоскости, прове-

денной через прямую с заданной плоскостью. Т.е. тенью прямой на плоскость является пря-

мая линия. Поэтому для построения тени прямой на плоскость, достаточно построить тени двух ее точек.

Если же тень от прямой падает на две плоскости, то она имеет точку излома, лежа-

щую на линии пересечения плоскостей. В данном случае точка излома лежит на оси (рису-

нок 4.4). Для ее нахождения, необходимо строить мнимую тень (В1t), т.е. определить гори-

зонтальный след луча проведенного через точку В.

Рисунок 4.4 29