Матан5

Монотонность и непрерывность. Теорема об обратной функции.

Теорема: Если монотонно возр. функция на [a;b] имеет разрыв в точке x₀, то f(x₀-)f(x₀)f(x₀+)

(может быть только скачёк)

Следование: Если функция монотонно возрастает на отрезке и не пропускает промежуточных значений, то эта функция непрерывна.

Теорема: (об обратной функции) Если функция строго возрастает и непрерывна на отрезке, то у неё имеется обратная функция, которая тоже возрастает и непрерывна.

Если функция строго убывает и непрерывна на отрезке, то у неё имеется обратная функция, которая тоже убывает и непрерывна.

Непрерывность элементарных функций.

def 1 / Простейшими элементарными функциями называются: const, e^x, lnx, x^, sinx, cosx, tgx, ctgx, arcsinx, arccosx, arctgx, arcctgx

def 2 / Элементарные функции называются все те функции, которые получаются из простейших при помощи конечного числа арифметических операций.

Теорема: Любая элементарная функция непрерывна в каждой точке где она определена.

Определение производной. Её геометрический и физический смысл.

def / Рассмотрим предел отношения приращения функции и вызвавшему его приращения аргумента при условии, что x0. Если этот предел сущ., то он называется производной функции f в точке x.

limy/x=df(x)/dx=tg=f (x)

В механике производная – мгновенная скорость

S (t)=V(t) V (t)=a(t)

Дифференцируемые функции и их свойства.

def 1 / Функция f называется дифф-ой в точке x, если f=f(x+x₀)-f(x)=Ax+o(x) при x0 можно представить в виде суммы двух слагаемых из которых 1^ое – линейно относительно x, а 2^ое явл. бесконечно малой более высокого порядка.

def 1 / Если функция дифф-ма, то главная часть её приращения (Аx) называется дифференциалом.

Теорема 1. Для того, чтобы функция была дифф-ма в точке, необходимо и достаточно чтобы в этой точке сущ. конечная производная, при этом дифф-ал функции df(x)=f (x) x (т.е. A=f (x))

Теорема 2. Если f(x) дифф-ма в точке, то она непрерывна в этой точке. Обратное утверждение неверно.

Правила дифференцирования.

1) Пр. дииф-ия обратных функций:

y=g(x) – функция обратная к f – дифференцируема и f 0 ни в одной точке.

g (x)=1/f (g(x))

x=f(y) обратная- y=g(x)

Док-во: x=f(y)=f(g(x))  1=f (g(x))g (x)  g (x)=1/f (g(x))

2) Пр. дифф-ия функций заданных параметрическим способом.

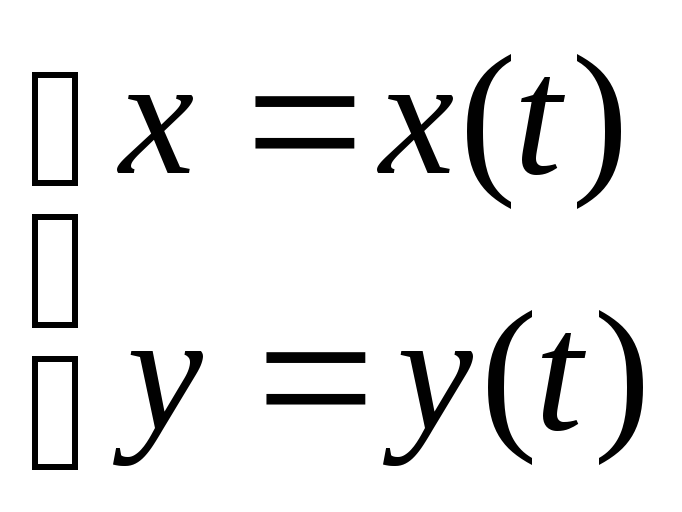
Предположим, что x(t) и y(t) обе дифф-мы, x(t) имеет обратную.

x (t)0 t=t(x) – обратная y=y(t(x))

y_x=y (t(x))t (x)=y_tt_x=y_t/x_t

Теорема о среднем значении.

Лемма Ферма:

def / x₀ называется точкой max f , если  окрестность этой точки ( x₀ ): xx₀ f(x)f(x₀)

xпроколотой окрестности x₀ f(x)<f(x₀), то x₀ - строгий max.

Аналогично определяется точка min f и точка строгого min.

Лема Ферма: (необходимое усл. экстремума)

Если в точке extr f (x₀), то эта производная = 0

Это усл. не является достаточным для наличия extr в точке.

Док-во: Пусть x₀ – точка max f и пусть f (x₀) сущ.

Для достаточно малых h f(x₀+h)-f(x₀)0

1) h<0 (f(x₀+h)- f(x₀))/h0 , h0 f (x₀)0

2) h>0 (f(x₀+h)- f(x₀))/h0 , h0 f (x₀)0

Общий вывод : f (x₀)=0

Недостаточность : контр пример f(x)=x³

f (x)=3x²=0

x=0 (на графике видно, что это не extr)

Теорема 1. (Т. Ролля)

Пусть fC[a;b]D(a;b)

Если f(a)=f(b), то c(a;b): f (c)=0

Док-во: Т.к. функция непрерывна на отрезке, то по теореме Вейштрасса на этом отрезке она достигает своё наименьшее или наибольшее значение.

1) Предположим, что и max и min на двух концах, то f(x)=const f (x)=0

2) Или max, или min строго внутри (a;b)

Допустим max

Т.к. точка max внутри, то и f (x₀) по усл., т.к. f дифф-ма внутри (a;b)

c(a;b): f (c)=0 по лемме Ферма.

Теорема 2. (Т. Лагранжа)

Пусть fC[a;b]D(a;b)

Тогда c(a;b): f (c)=(f(b)-f(a))/(b-a)

f(b)-f(a)=(b-a)f (c) Приращение функции равно приращению аргумента, умноженному на значение производной в некоторой промежуточной точке отрезка.

Теорема 3. (Т. Коши)

Пусть f,gC[a;b]D(a;b), g (x)0 x(a;b)

Тогда c(a;b): f (c)/g (c)=(f(b)-f(a))/(g(b)-g(a))

Замечание: 1. Из Т. Ролля следует, что g(b)-g(a)0

2. Пусть g(x)=x  f (c)=(f(b)-f(a))/(b-a) Теорема Лагранжа частный случай теоремы Коши.

Формула Тейлора.

Лемма 1.

Пусть f в точке a имеет производную до n^ого порядка включительно.

fDⁿ(a)

P_n(x)=C_k(x-a)_k , (k=0,…,n) :

P_n(a)=f(a)

P_n(a)=f (a)

…………..

P_n⁽ⁿ⁾(a)=f ⁽ⁿ⁾(a)

Док-во:

P_n(a)=C₀+0=f(a)

P_n(x)=1C₁+2C₂(x-a)+3C₃(x-a)²+…+nC_n(x-a)^n-1

P_n(a)=C₁=f (a)

P_n(x)=2!C₂+2*3C₃(x-a)+…+n(n-1)C_n(x-a)^n-2

P_n(a)=2!C₂=f (a)

n!C_n=f ⁽ⁿ⁾(a)

P_n(x)=(f ^(k)(a)/k!)*(x-a)^k , (k=0,…,n) – многочлен Тейлора.

o((x-a)ⁿ), xa – остаточный член в форме Пеана.

R_n(f,a;x)= (f ⁽ⁿ⁺¹⁾(c)/(n+1)!)*(x-a)ⁿ⁺¹ – остаточный член в форме Лагранжа, где c между a и x

Правило Лопиталя-Бернулли.

Раскрытие неопределённости вида (0/0),(/)

Теорема 1. Пусть f,gD(a,a+), >0;

g (x)0 x(a,a+); f(a+)=0, g(a+)=0

Тогда (если limf (x)/g (x)=L , xa+)  (обязательно limf(x)/g(x)=L , xa+)

Обратное не верно.

# Контр пример (f(x)=x²sin(1/x) g(x)=x (0,) )

lim(f(x)/g(x))=lim(xsin(1/x))=0, x0+

lim(f (x)/g (x))=lim(2xsinx-cos(1/x))=не сущ.

Для левого предела теорема аналогична.

Теорема верна, когда x

Формулируется точно так же когда неопределённость вида (/)