
Funktsionalny_analiz
.docx№1)
Для любых 2-х элементов x,y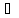 L
однозначно определён элемент z
L
однозначно определён элемент z L,
называемый их суммой и обозначаемый
x+y,
причём: 1)x+y=y+x
(коммутативность); 2)x+(y+z)=(x+y)+z
(ассоциативность); 3)В L
существует элемент 0 такой, что x+0=0+x=x,
L,
называемый их суммой и обозначаемый
x+y,
причём: 1)x+y=y+x
(коммутативность); 2)x+(y+z)=(x+y)+z
(ассоциативность); 3)В L
существует элемент 0 такой, что x+0=0+x=x,
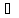 x
x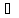 L;
4)
L;
4)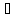 x
x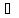 L
существует элемент (-x)
L
существует элемент (-x)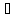 L
такой, что x+(-x)=0.
L
такой, что x+(-x)=0.
№2)
Для любого числа α и
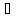 x
x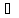 L
определён элемент αx
L
определён элемент αx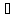 L,
причём: 1)α(βx)=(αβ)x;
2)1*х=х.
L,
причём: 1)α(βx)=(αβ)x;
2)1*х=х.
№3) Указанные выше операции сложения элементов и умножения элементов на число связаны дистрибутивными законами: 1) (α+β)x=αx+βx; 2)α(x+y)= αx+αy.
Зависимость того, какие числа α,β,… используются, различают действительные и комплексные линейные пространства.
(О2)
Линейные пространства L
и L*
называют изоморфными, если между их
элементами можно установить взаимно
однозначное соответствие, согласованное
с операциями в L
и L*,
т.е. если х↔х*, y↔y*,
то x+y↔x*+y*,
αх↔αх*, где x,y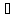 L,
х*,y*
L,
х*,y*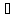 L*.
L*.
Элементы x,y,…,w линейного пространства линейно зависимы, если существуют такие числа α,β,…,λ не все равные нулю, что αx+βy+…+λw=0. В противном случае эти элементы называются линейно независимыми, т.е. если αx+βy+…+λw=0, то α=β=…=λ=0.
Бесконечная система элементов x,y,… пространства L называется линейно независимой, если любая её конечная подсистема линейно независима.
Если в L существует n линейно независимых элементов, а любые n+1 элементов линейно зависимы, то говорят, что пространство L имеет размерность n.
Если в L можно указать систему из произвольного конечного числа линейно независимых элементов, то говорят, что L бесконечномерно.
Базисом в n-мерном пространстве L называется любая система, состоящая из n линейно независимых элементов.
Непустое подмножество L’ линейного пространства L называется подпространством, если L’ само является линейным пространством по отношению к операциям, определённым в L.
№17) Линейные функционалы.
Числовую
функцию f,
определённую на линейном пространстве
L,
будем называть функционалом. Функционал
f
называется аддитивным, если f(x+y)=f(x)+f(y),
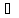 x,y
x,y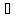 L.
Функционал называется однородным, если
f(αx)=αf(x)
(α – произвольное число). Аддитивный
однородный функционал называется
линейным функционалом. Он удовлетворяет
условию f(αx+βy)=αf(x)+βf(y).
L.
Функционал называется однородным, если
f(αx)=αf(x)
(α – произвольное число). Аддитивный
однородный функционал называется
линейным функционалом. Он удовлетворяет
условию f(αx+βy)=αf(x)+βf(y).
(П1)
Интеграл
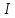 (x)=
(x)= – линейный функционал в пространстве
C[a,b].
– линейный функционал в пространстве
C[a,b].
(П2)
Пусть y0(x)
– фиксированная непрерывная функция
на [a,b].
Для любой непрерывной функции из C[a,b]
положим
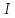 (x)=
(x)=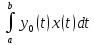 – линейный функционал в C[a,b].
– линейный функционал в C[a,b].
Определённый
на L
функционал p
называется выпуклым, если
P(αx-(1-α)y)≤p(αx)+(1-
α)p(y),
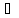 x,y
x,y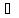 L,
0≤α≤1.
L,
0≤α≤1.
Пусть
на подпространстве L0
линейного пространства L
задан линейный функционал f0.
Линейный функционал f,
определённый на всём L,
называется продолжением функционала
f0,
если f(x)=f0(x)
при x L0.
Задачи по продолжению линейных
функционалов часто встречаются в мат
анализе. Основную роль здесь играет
следующая теорема.
L0.
Задачи по продолжению линейных
функционалов часто встречаются в мат
анализе. Основную роль здесь играет
следующая теорема.
(Т1)
(Теорема Хана – Банаха) Пусть p
– конечный выпуклый функционал,
определённый на действительном линейном
пространстве L
и пусть L0
– линейное подпространство в L.
Если f0
линейный, определённый в L0,
удовлетворяющий условию f0(x)≤p(x)
и на L.
(ДОКАЗАТЕЛЬСТВО) Покажем, что если L0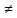 L,
то функционал f0
можно продолжить на некоторое «большее»
пространство L’
с сохранением условия f0(x)≤p(x).
Пусть z
– произвольный элемент из L,
не принадлежащий L0.
Пусть L’
– подпространство, каждый элемент
которого имеет вид x+tz, где z
L,
то функционал f0
можно продолжить на некоторое «большее»
пространство L’
с сохранением условия f0(x)≤p(x).
Пусть z
– произвольный элемент из L,
не принадлежащий L0.
Пусть L’
– подпространство, каждый элемент
которого имеет вид x+tz, где z L0,
х
L0,
х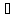 L0,
t
– любое действительное число. Если
f1(x)
– искомое продолжение f0
на L’
, то f1(x+tz)
= f0(x)
+ tc.
Обозначим f1(z)=c;
Имеем f1(x+tz)=f0(x)
+ tc.
Выберем число с так, чтобы условие (1)
выполнялось на L’,
т.е. чтобы для любого х ∈
L0
и для любого t∈R
выполнялось неравенство f1(x+tz)≤p(x+tz),
т.е. f0(x)
+ tc≤p(x+tz).
L0,
t
– любое действительное число. Если
f1(x)
– искомое продолжение f0
на L’
, то f1(x+tz)
= f0(x)
+ tc.
Обозначим f1(z)=c;
Имеем f1(x+tz)=f0(x)
+ tc.
Выберем число с так, чтобы условие (1)
выполнялось на L’,
т.е. чтобы для любого х ∈
L0
и для любого t∈R
выполнялось неравенство f1(x+tz)≤p(x+tz),
т.е. f0(x)
+ tc≤p(x+tz).
Отсюда имеем:
При
t>0:f0( )+c≤p(
)+c≤p(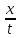 +z),
т.е c≤p(
+z),
т.е c≤p(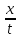 +z)
– f0(
+z)
– f0(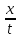 ).
).
При
t<0:f0(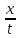 )+c≥
- p(
)+c≥
- p(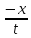 - z),
т.е c≥
- p(-
- z),
т.е c≥
- p(-
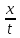 - z)
– f0(
- z)
– f0(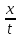 ).
).
Покажем, что число с, удовлетворяющее этим 2-м условиям, существует.
Пусть y1,y2 – произвольные элементы из L0. Тогда f0(y2 – y1) = f0(y2)- f0(y1)≤p(y2 – y1)=p((y2 +z)-(y1+z))≤p(y2 +z) – p(y1+z) = p(y2 +z) + p(-y1-z). Отсюда f0(y2) – p(y2 +z)≤ f0(y1) + p(-y1 -z), т.е. f0(-y2)+p(y2 +z)≥- f0(y1) – p(-y1 -z).
Обозначим sup(-f0(y1)-p(-y1 -z)) = c1, inf(-f0(y2)+p(y2+z))=c2.
Отсюда c1≤c2. Выберем число с так, чтобы c1≤с≤c2. Определим функционал f1(x) на L’ по формуле f1(x+tz)=f0(x)+tc.
Этот функционал удовлетворяет условию (1)
Итак,
мы показали, что если функция f0
определена на подпространстве L0 L
и удовлетворяет на L0
условию (1), то f0
можно продолжить на «большее» пространство
L’,
сохранив условие (1).
L
и удовлетворяет на L0
условию (1), то f0
можно продолжить на «большее» пространство
L’,
сохранив условие (1).
Если в L можно выбрать счетную сумму элементов z1,z2,…,zn,… не принадлежащих L0 и порождающую всё L, то функционал на L строим по индукции, рассматривая цепочку подпространств {L0,z1} = L(1), {L1,z2} = L(2),… .
Тогда
каждый элемент x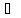 L
войдет в некоторое подпространство
L(n),
условие (1) будет выполнено, т.е. функционал
f(x)
будет продолжен на всё L.
L
войдет в некоторое подпространство
L(n),
условие (1) будет выполнено, т.е. функционал
f(x)
будет продолжен на всё L.
В общем случае доказательство завершается применением Леммы Цорна (ДОК).
№18) Нормированные пространства.
(О1)
Векторное пространство L
называется нормированным пространством,
если
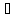 x∈L
определено действительное число ||x||,
называемое нормой, причём, норма
удовлетворяет аксиомам: 1) ||x||≥0,
x∈L
определено действительное число ||x||,
называемое нормой, причём, норма
удовлетворяет аксиомам: 1) ||x||≥0,
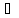 х∈L;
||x||=0
т т т, когда х=0; 2) ||x+y||≤||x||+||y||,
х∈L;
||x||=0
т т т, когда х=0; 2) ||x+y||≤||x||+||y||,
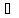 x,y∈L;
3) ||αx||=||α||
||x||,
x,y∈L;
3) ||αx||=||α||
||x||,
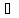 x∈L,
x∈L,
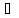 α∈R.
α∈R.
Всякое
нормированное пространство становится
метрическим пространством, ели положить
ρ(x,y)=||x-y||;
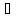 x,y∈L.
Так что нормированное пространство –
частный случай метрических пространств.
x,y∈L.
Так что нормированное пространство –
частный случай метрических пространств.
После
введения метрики естественным образом
определяется сходимостью элементов
нормированного пространства, а именно
 =
x,
если
=
x,
если
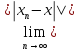 = 0. Определённая таким образом сходимость
в нормированном пространстве называется
сходимостью по норме. Полное нормированное
пространство называется пространством
Банаха или Банаховым пространством или
пространством типа В.
= 0. Определённая таким образом сходимость
в нормированном пространстве называется
сходимостью по норме. Полное нормированное
пространство называется пространством
Банаха или Банаховым пространством или
пространством типа В.
(П1) Прямая R – полное нормированное пространство, ||x||=|x|, ρ(x,y)=||x-y||=|x-y|.
(П2)
Rn
– пространство типа В, ||x||=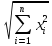 ,
метрика совпадает с параграфом 1.
,
метрика совпадает с параграфом 1.
(П3)
C[a,b]
– пространство типа В, ||f||=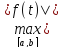 .
.
Подпространство
L0
линейного пространства L
обладает свойством: если x,y∈L0,
то αx+βx∈L0,
 α,β∈R.
Под подпространством нормированного
пространства понимается замкнутое
пространство. В частности под
подпространством порождаемым системой
элементов {xα}
понимается наименьшее замкнутое
пространство, содержащее {xα}.
Такое подпространство называется
линейным замыканием системы {xα}.
α,β∈R.
Под подпространством нормированного
пространства понимается замкнутое
пространство. В частности под
подпространством порождаемым системой
элементов {xα}
понимается наименьшее замкнутое
пространство, содержащее {xα}.
Такое подпространство называется
линейным замыканием системы {xα}.
Незамкнутую совокупность элементов, содержащую вместе с x,y их произвольную комбинацию αx+βy, назовём линейным многообразием. Произвольная система, лежащая в нормированном пространстве E, называется полной, если порождённая ею замкнутое подпространство есть всё Е.
№19) Евклидовы пространства.
Для введения нормы в линейных пространствах широко используется скалярное произведение.
(О1) Скалярным произведением в действительном пространстве L называется действительная функция (x,y), определённая для каждой пары x,y∈L и удовлетворяющая аксиомам: 1) (x,y)=(y,x); 2) (x,y1+y2)=(x,y1) + (x,y2); 3) (λx,y)= λ(x,y); 4) (x,x)≥0, (x,x)=0 т т т, когда x=0.
Линейное
пространство заданным в нём скалярным
произведением называется Евклидовым
пространством. Норма в Евклидовом
пространстве задаётся по формуле
||x||=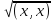 .
Все аксиомы нормы выполняются в силу
аксиом 1) – 4). Для проверки аксиомы 2)
используется неравенство Коши –
Буняковского: |(x,y)|≤||x||
||y||
(1). Для доказательства неравенства (1)
рассмотрим трёхчлен от действительной
переменной α.
.
Все аксиомы нормы выполняются в силу
аксиом 1) – 4). Для проверки аксиомы 2)
используется неравенство Коши –
Буняковского: |(x,y)|≤||x||
||y||
(1). Для доказательства неравенства (1)
рассмотрим трёхчлен от действительной
переменной α.
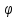 (λ)*(λx+y,λx+y)=(λx+y,λx)+(λx+y,y)=
(λx,λx+y)
+ (y,λx+y)
= (λx,λx)
+ 2(λx,y)
+ (y,y)
= λ2(x,x)
+ 2λ(x,y)
+ (y,y)
= λ2||x||2
+ 2λ(x,y)
+ ||y||2
≥0. Дискриминант этого трёхчлена (x,y)2
- ||x||2||y||2
≤ 0. Отсюда следует (1).
(λ)*(λx+y,λx+y)=(λx+y,λx)+(λx+y,y)=
(λx,λx+y)
+ (y,λx+y)
= (λx,λx)
+ 2(λx,y)
+ (y,y)
= λ2(x,x)
+ 2λ(x,y)
+ (y,y)
= λ2||x||2
+ 2λ(x,y)
+ ||y||2
≥0. Дискриминант этого трёхчлена (x,y)2
- ||x||2||y||2
≤ 0. Отсюда следует (1).
Наличие
в линейном пространстве L
скалярного произведения позволяет
определить угол между векторами: cos(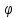 )=
)=
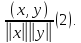 Из
неравенства Коши – Буняковского следует
cos(
Из
неравенства Коши – Буняковского следует
cos(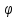 )≤1,
0≤
)≤1,
0≤
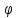 ≤
≤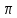 .
Если (x,y)
= 0, то cos(
.
Если (x,y)
= 0, то cos(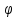 )=0,
)=0,
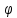 =
=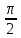 .
В этом случае векторы
x,y
называются ортогональными. Система
векторов {
.
В этом случае векторы
x,y
называются ортогональными. Система
векторов {
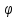 α}
ненулевых векторов называется
ортогональной, если (
α}
ненулевых векторов называется
ортогональной, если (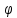 α,
α, β)=0,
α
β)=0,
α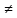 β.
Если векторы {xα}
образует ортогональную систему, то они
линейно независимы. Если
a1
β.
Если векторы {xα}
образует ортогональную систему, то они
линейно независимы. Если
a1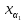 +
a2
+
a2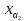 +…+
an
+…+
an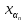 =0,
то
(
=0,
то
( ,
a1
,
a1 +
a2
+
a2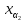 +…+
an
+…+
an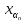 )=
a1(
)=
a1(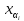 ,
,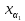 )
+ a2(
)
+ a2( ,
, )
+ … + an(
)
+ … + an(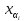 ,
, )
= ai(
)
= ai(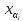 ,
,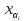 )
= 0. Т.к.
(
)
= 0. Т.к.
(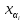 ,
, )
)
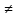 0, ai=0,
i=
0, ai=0,
i=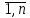 .
Если система {xα}
является полной, т.е. порождённое ею
замкнутое подпространство совпадает
с L,
то она называется ортогональным базисом.
Если при этом норма каждого элемента
равна единице, то система {xα}
называется ортогональным нормированным
базисом.
.
Если система {xα}
является полной, т.е. порождённое ею
замкнутое подпространство совпадает
с L,
то она называется ортогональным базисом.
Если при этом норма каждого элемента
равна единице, то система {xα}
называется ортогональным нормированным
базисом.
(П1)
Rn
, (x,y)=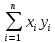 – Евклидово пространство. Аксиомы
скалярного произведения проверяются
непосредственно. Ортогональный базис
образуют, например: e1(1,0,..,0,…0),
e2(0,1,0,…,0,…,0),…,en=(0,…,0,1).
– Евклидово пространство. Аксиомы
скалярного произведения проверяются
непосредственно. Ортогональный базис
образуют, например: e1(1,0,..,0,…0),
e2(0,1,0,…,0,…,0),…,en=(0,…,0,1).
(П2)
L2
, (x,y)= – Евклидово пространство. Аксиомы
скалярного произведения проверяются
непосредственно. Ортогональный базис
образуют, например: e1(1,0,..,0,…0,…),
e2(0,1,0,…,0,…,0,…),…,en=(0,…,0,1,0,…),….
– Евклидово пространство. Аксиомы
скалярного произведения проверяются
непосредственно. Ортогональный базис
образуют, например: e1(1,0,..,0,…0,…),
e2(0,1,0,…,0,…,0,…),…,en=(0,…,0,1,0,…),….
№20) Гильбертово пространство.
(О1) Полное сепарабельное Евклидово пространство бесконечного числа измерений называется Гильбертовым пространством. Итак, совокупность H элементов f,g,… произвольной природы называется Гильбертовым пространством, если: 1) H – Евклидово пространство, т.е. линейное пространство со скалярным произведением; 2) H является полным в смысле метрики ρ(f,g)=||f-g||; 3) H бесконечномерно, т.е. в нём для любого натурального n найдётся n линейно независимых элементов; 4) Н сепарабельно, т.е. в нём существует счётное всюду плотное множество.
Примером Гильбертова пространства может служить пространство l2.
Два евклидовых пространства E и E* называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие так, что если x↔x*, y↔y*, где x,y∈E, x*,y*∈E*, то x+y↔x*+y*, αx↔αx*, (x,y)↔(x*,y*). Любые два n-мерных Евклидовых пространства изоморфны между собой и, следовательно, изоморфны Rn. Однако, Евклидовы пространства бесконечного числа измерений не всегда изоморфны друг другу.
(Т1)
Любые два Гильбертовых пространства
изоморфны между собой. (ДОКАЗАТЕЛЬСТВО)
Покажем, что любое Гильбертово пространство
Н изоморфно пространству l2.
Выберем в Н произвольную полную
ортогональную нормированную систему
{φn}.
Элементу f∈Н
поставим в соответствие последовательность
{c1,c2,…,cn,…}∈l2.
(Обратно) По теореме Рисса - Фишера
всякому элементу {c1,c2,…,cn,…}∈l2
соответствует некоторый элемент f∈H,
для которого числа c1,c2,…,cn,…
являются его коэффициентами Фурье. Т.о.
установленное нами соответствие между
элементами из Н и l2
взаимно однозначно. Если элемент f
‘↔(c1’,c2’,…,cn’,…),
f
‘’↔ (c1’’,
c2’’,…,
cn’’,…),
то f
‘+f
‘’↔( c1’+c1’’,c2’+c2’’,…,cn’+cn’’,…),
αf
‘↔(αc1’,αc2’,…,αcn’,…).
Воспользовавшись равенством Парсеваля,
имеем (f
‘,f
‘)=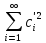 ,
(f
‘’,f
‘’)=
,
(f
‘’,f
‘’)=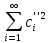 ,
(f
‘+f
‘’,f
‘+f
‘’)= (f
‘,f
‘) +2(f
‘,f
‘’)+ (f
‘’,f
‘’)=
,
(f
‘+f
‘’,f
‘+f
‘’)= (f
‘,f
‘) +2(f
‘,f
‘’)+ (f
‘’,f
‘’)=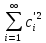 +2(f
‘,f
‘’)+
+2(f
‘,f
‘’)+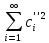 =
=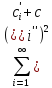 =
=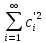 +
+ +
+ .
Отсюда (f
‘,f
‘’)=
.
Отсюда (f
‘,f
‘’)=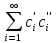 .
Здесь слева скалярное в Н, а справа
скалярное произведение в l2.
(ДОК)
.
Здесь слева скалярное в Н, а справа
скалярное произведение в l2.
(ДОК)
(ВЫВОД) Итак, с точностью до изоморфизма существует только одно Гильбертово пространство l2.
№21) Характеристическое свойство Евклидовых пространств.
Пусть Х – нормированное пространство. Какова должна быть норма в Х, чтобы оно было Евклидовым пространством?
(Т1) Чтобы нормированное пространство Х было Евклидовым необходимо и достаточно, чтобы в нём для любых 2-х элементов f и g выполнялось равенство ||f+g||2 + ||f-g||2 = 2(||f||2 + ||g||2) (1). (ДОКАЗАТЕЛЬСТВО) (необходимость) Пусть Х – Евклидово пространство. Т.к. f+g и f-g – диагонали параллелограмма, построенного на сторонах f и g, то равенство (1) выражает свойство параллелограмма в Евклидовом пространстве: сумма квадратов диагоналей равна сумме квадратов всех его сторон. (ДОК)
(П1)
Рассмотрим пространство
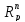 с нормой ||x||p
=
с нормой ||x||p
=
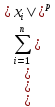 ,
p≥1.
Из всех таких пространств, которых
бесконечное множество, лишь одно, а
именно при p=2,
будет Евклидовым.
,
p≥1.
Из всех таких пространств, которых
бесконечное множество, лишь одно, а
именно при p=2,
будет Евклидовым.
Действительно,
рассмотрим в
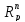 два вектора f=(1,1,0,..,0)
и g=(1,-1,0,…,0)
два вектора f=(1,1,0,..,0)
и g=(1,-1,0,…,0)
||f+g||2 + ||f-g||2 = 2(||f||2 + ||g||2)-основной критерий евклидова пространства.
f+g=(2,0,…,0),f-g=(0,2,0,…,0)
||f+g||р=2, ||f-g||р=2
||f||р=21/р, ||g||р=21/р
Значит по формуле (1) должно выполняться равенство:22+22=2(22/р+22/р),4=2*22/р,2=22/р=>2/p=1,p=2
(П2)С[a,b]-множество
непрерывных функций.Возьмем
f(t)=cost,g(t)=sint,
C[0,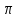 /2]
/2]
||f||=1,
||g||=1
||f+g||=max[0, /2]
|cost+sint|=
/2]
|cost+sint|=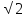 {-sint+cost=0 tgt=1 t=
{-sint+cost=0 tgt=1 t=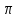 /4
cos
/4
cos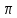 /4+sin
/4+sin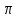 /4=
/4=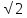 cos0+sin0=1 Cos
cos0+sin0=1 Cos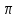 /2+sin
/2+sin /2=1}
/2=1}
||f-g||=
max[0,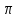 /2]
|cost-sint|=1 { -sint-cost=1 -cos=1 tgt=-1-критических
т.
нет
cos0-sin0=1 cos
/2]
|cost-sint|=1 { -sint-cost=1 -cos=1 tgt=-1-критических
т.
нет
cos0-sin0=1 cos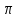 /2-sin
/2-sin /2=-1
}
/2=-1
}
По
равенству (1) имеем:2+12≠2(1+1)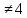 3≠4
3≠4
Таким
образом норму пространства C[0,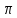 /2]
нельзя задать с
помощью какого бы то ни было скалярного
произведения,т.е. C[a,b]
не является евклидовым пространством.
/2]
нельзя задать с
помощью какого бы то ни было скалярного
произведения,т.е. C[a,b]
не является евклидовым пространством.
22) Комплексные евклидовые пространства.
На
ряду с действительными можно определить
и комплексное евклидово пространство,
однако аксиомы 1-4 действительного
евклидового пространства в комплексных
пространствах не могут быть выполнены
одновременно. Действительно, из аксиом
1 и 3 следует, что (αx;αx)=α(xαx)=α(αx,x)=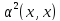
Если x=i, то (ix,ix)=-(x,x)
Аксиомы 1 и 3 оказались не совместимыми с аксиомами 4.
В комплексных пространствах скалярное произведение определяется как числовая комплексно-значная функция удовлетворяющая аксиомам:
-
(x,y)=
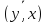
-
(
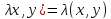
-
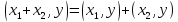
-
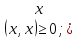 ,x)=0↔x=0
,x)=0↔x=0
Из
аксиом 1 и 2 имеем: (x,𝛌y)=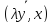 =
=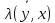 =
=
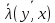 =
=

Теперь
: (ix,ix)=i(x,ix)=i =i*
=i*
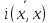 =i*
=i*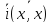 =(x,x)≥0
=(x,x)≥0
1)Линейное
пространство
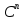 совокупность
элементов x(
совокупность
элементов x(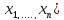 c
комплексными координатами и с операцией
умножение на комплексные числа. Скалярное
произведение двух элементов x
и y=(
c
комплексными координатами и с операцией
умножение на комплексные числа. Скалярное
произведение двух элементов x
и y=( определяется формулой:
определяется формулой:
(x,y)=

Всякое
комплексное евклидово пространство
размерности n,
изоморфно этому пространству
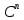 .
.
2)Пространство
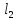 ,
в котором элементы – это последовательности
(x1,…,xn,..),
удовлетворяющее условию:
,
в котором элементы – это последовательности
(x1,…,xn,..),
удовлетворяющее условию:
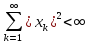
Скалярное
произведение: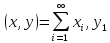
3)
Пространство
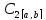 -
комплексно-значных непрерывных функций,
определенных на сегменте [a,b]
со скалярным произведением (f,g)=
-
комплексно-значных непрерывных функций,
определенных на сегменте [a,b]
со скалярным произведением (f,g)=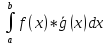
В комплексном евклидовом пространстве длина (норма) вектора определяется как и в действительном случае формулой:
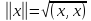
Понятие
угла между векторами обычно вводится,
т. К. величина
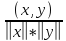 вообще говоря, комплексна и не может
быть косинусом какого нибудь действительного
угла.
вообще говоря, комплексна и не может
быть косинусом какого нибудь действительного
угла.
Понятие ортогональности сохраняется:если (x,y)=0,то х и у называются ортогональными.
Если
{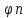 }
какая-нибудь ортогональная система в
комплексно евклидовом пространстве Е
и f-какой-нибудь
элемент из Е,то как и в действительном
случае,числе аn=(f,
}
какая-нибудь ортогональная система в
комплексно евклидовом пространстве Е
и f-какой-нибудь
элемент из Е,то как и в действительном
случае,числе аn=(f,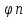 )/
)/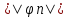 называется коэфициентами Фурье,а ряд
называется коэфициентами Фурье,а ряд
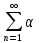 nan-рядом
Фурье элемента f.
nan-рядом
Фурье элемента f.
По
ортогональной системе
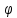 n.
Справедливо неравенство Бесселя:
n.
Справедливо неравенство Бесселя: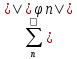 2*an2<(f,f).
2*an2<(f,f).
В
частности,если система {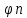 }
ортонормированна, то коэффициенты Фурье
Сn(f,
}
ортонормированна, то коэффициенты Фурье
Сn(f,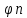 )
и неравенство Бесселя принимается
вид:
)
и неравенство Бесселя принимается
вид: n2
<(f,f).
n2
<(f,f).
Полное сепарабельное комплексное пространство бесконечной размерности называется комплексно гильбертовым пространством.
Все комплексно гильбертовы пространства изоморфны между собой. Все теоремы доказанные выше для действительных евклидовых пространств справедливы и для комплексных пространств.(с незначительными изменениями, учитывающими комплексность скалярного произведения)
 23 Линейные операторы.
23 Линейные операторы.
О1:Множество Т называется линейным топологическим пространством,если:1)Т-линейное пространство,2)Т-топологическое пространство,3)операции сложение и умножение на число непрерывны относительно заданной в Т топологии
Пусть Тх и Ту-два линейных топологических пространства одновременно вещественных или комплексных.
Линейным
оператором, действующим из Тх
в Ту
называется отображение у=Ах, х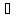 Тх ,у
Тх ,у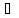 Ту,
удовлетворяющее условиям:1)отображение
аддитивное ,т.е. А(х1+х2)=
Ах1+А
х2,2)отображение
однородно ,т.е. А(
Ту,
удовлетворяющее условиям:1)отображение
аддитивное ,т.е. А(х1+х2)=
Ах1+А
х2,2)отображение
однородно ,т.е. А(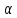 х)=
х)=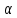 Ах
для всех х и всех
Ах
для всех х и всех
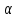 .Иначе говоря, оператор А-линеен, если
А(
.Иначе говоря, оператор А-линеен, если
А( х1+
х1+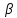 х2)=
х2)=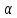 Ах1+
Ах1+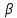 Ах2-для
всех х1 и
х2
и всех
Ах2-для
всех х1 и
х2
и всех
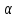 и
и
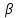 .
.
Совокупность
DА
тех х Тх
,для кот. Оператор А определен называется
областью определения оператора А.
Тх
,для кот. Оператор А определен называется
областью определения оператора А.
Не
предполагается, что DА=Тх,
однако DА
будем всегда
считать линейным многообразием,т.е.,если
х1
и х2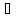 DА,то
DА,то
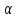 х1+
х1+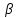 х2
х2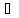 DА
при всех
DА
при всех
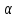 и
и
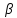 .
.
Оператор
А называется непрерывным в т.х0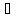 DА,
если для любой окрестности V
т. у0=Ах0
DА,
если для любой окрестности V
т. у0=Ах0
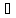 окрестность U
т.х0
такая,что,если х
окрестность U
т.х0
такая,что,если х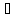 U
U
 DА,
то у=Ах
DА,
то у=Ах
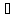 V.
V.
Оператор
называется непрерывным, если он непрерывен
в каждой т.х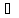 DА.
DА.
Ясно,что
для случая метрических пространств
непрерывность оператора означает,что
для любого
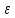 >0
>0
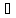
 >0
такое,что образ шара S(х,
>0
такое,что образ шара S(х,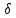 )
лежит в шаре S
(Ax,
)
лежит в шаре S
(Ax,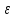 )
)
(П1)
Пусть Тх
– линейное топологическое пространство.
Положим, Ах=х,
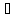 х∈Тх.
Оператор, переводящий каждый элемент
пространства в себя, называется единичным
оператором. Обычно единичный оператор
обозначают через букву
х∈Тх.
Оператор, переводящий каждый элемент
пространства в себя, называется единичным
оператором. Обычно единичный оператор
обозначают через букву
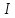 .
.
(П2)
Путь Тх
и Тy
– линейные топологические пространства.
Положим Ах=0,
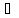 х∈Тх,
где 0 – нулевой элемент пространства
Тy.
Такой оператор называется нулевым
оператором.
х∈Тх,
где 0 – нулевой элемент пространства
Тy.
Такой оператор называется нулевым
оператором.
(П3)
Один из важнейших для анализа операторов
– оператор дифференцирования. а)Рассмотрим
пространство C[a,b]
и оператор Df=f
’(x),
действующий в C[a,b].
Этот оператор определён не на всём
C[a,b],
а только на линейном многообразии
функций, имеющих непрерывную производную.
Оператор D
линеен, но не является непрерывным.
Например, последовательность
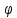 n(x)=
n(x)=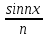 сходится в метрике пространства C[a,b]
к нулю, однако D
сходится в метрике пространства C[a,b]
к нулю, однако D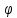 n(x)=cosnx
не сходится. б)Оператор D
можно рассматривать на пространстве
C’[a,b]
непрерывно дифференцируемых функций
с нормой ||f||=
n(x)=cosnx
не сходится. б)Оператор D
можно рассматривать на пространстве
C’[a,b]
непрерывно дифференцируемых функций
с нормой ||f||=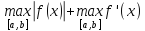 .
Оператор отображает C’[a,b]
в C[a,b].
В этом случае оператор D
линеен и непрерывен и отображает всё
C’[a,b]
на всё C[a,b].
.
Оператор отображает C’[a,b]
в C[a,b].
В этом случае оператор D
линеен и непрерывен и отображает всё
C’[a,b]
на всё C[a,b].
(П4)
Рассмотрим y(t)
=
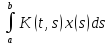 ,
где K(t,s)
непрерывное в квадрате a≤t,
s≤b
функция. Если x(t)∈C[a,b],
то y(t)∈C[a,b].
Значит оператор y=Ax
отображает C[a,b]
в себя. Этот оператор линеен. Действительно,
A(x1+x2)
=
,
где K(t,s)
непрерывное в квадрате a≤t,
s≤b
функция. Если x(t)∈C[a,b],
то y(t)∈C[a,b].
Значит оператор y=Ax
отображает C[a,b]
в себя. Этот оператор линеен. Действительно,
A(x1+x2)
=
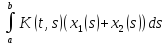 =
=
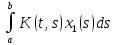 +
+
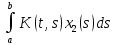 = Ax1
+ Ax2.
Однородность очевидна. Непрерывность.
Пусть функциональная последовательность
{xn(t)}
сходится к x(t)
в C[a,b].
Т.к. сходимость в C[a,b]
является равномерной сходимостью, то
под знаком интеграла можно переходить
к пределу
= Ax1
+ Ax2.
Однородность очевидна. Непрерывность.
Пусть функциональная последовательность
{xn(t)}
сходится к x(t)
в C[a,b].
Т.к. сходимость в C[a,b]
является равномерной сходимостью, то
под знаком интеграла можно переходить
к пределу
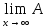 xn=
xn=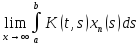 =
=
 =
=
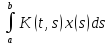 = Ах. Т.о. если xn
→ x,
то Ахn
→ Ах. доказано.
= Ах. Т.о. если xn
→ x,
то Ахn
→ Ах. доказано.
