
Глава 3. Операции над отображениями.
Умножение отображений
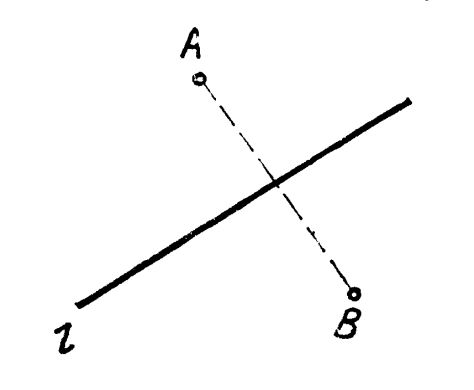
Пусть
имеются два отображения вида f:Х 7;g:Y
7;g:Y Z.
Выберем произвольный элемент х ϵ X
и применим к нему отображение f.
Под действием f
элемент х перейдет в элемент у = f{x)
из множества Y.
Если теперь к элементу у применить
отображение g",
то у перейдет в элемент z
= g(y)
из множества Z.
В результате каждому х
Z.
Выберем произвольный элемент х ϵ X
и применим к нему отображение f.
Под действием f
элемент х перейдет в элемент у = f{x)
из множества Y.
Если теперь к элементу у применить
отображение g",
то у перейдет в элемент z
= g(y)
из множества Z.
В результате каждому х Х
ставится в соответствие вполне
определенный элементz
= g(f(x))
множества Z
(рис. 3.7).
Х
ставится в соответствие вполне
определенный элементz
= g(f(x))
множества Z
(рис. 3.7).
Таким образом, последовательное применение отображений fug приводит к отображению множества X в множество Z, которое называется произведением (или композицией) отображений g и f. Так как произведение

отображений g и f переводит элемент хϵX в элемент g(f(x)), то это произведение естественно обозначать символом g о f или просто gf. По определению (g o f) (х) = g(f(x)) для любого х→Х. Отметим, что произведение отображений g:X' →Y' и f : X → Y
определено лишь в случае, когда X' = Y. В частности, может случиться, что gof определено, a fog не определено. Очевидно, если f u g — преобразования множества X, то определены оба произведения g o f и fog. Они также являются преобразованиями X.
Важнейшее свойство умножения отображений — его ассоциативность. Теорема 31. Пусть f, g, h — три таких отображения, что одно из произведений
(h°g)of, ho (gof)
определено. Тогда определено и другое произведение, причем
(hog)of = ho(gof).
Пусть, например, определено h o (gof). Если f:X→Y, то g должно быть отображением вида g:Y→Z. Но тогда gof:X→Z и, значит, h :Z→U.
Проверим, что (hog)o f тоже определено. Действительно, hog определено и ho g:Y→U Следовательно, определено и (hоg) о причем (hоg) о f : X→U.
Покажем теперь, что отображения (hog) o f и h о (gоf) равны,
т. е. для каждого хϵX Имеем
((hog) о f) (X) =(hog) (f(X)) = h(g(f(X))),
(ho (go f))(x) = h((g о f)(x)) = h(g(f(x))).
Опираясь
на понятие произведения двух отображений,
можно определить композицию трех,
четырех и более отображений. Пусть,
например,
 ,
, ,
...,
,
..., —преобразования
множестваX.
—преобразования
множестваX.
Их
произведение
 o
...o
o
...o определим индуктивно:
определим индуктивно:
 o
o уже определено,
уже определено,
 °
° °
° = /з ° (
= /з ° ( °
° )
и, вообще, еслиi
< k
и
)
и, вообще, еслиi
< k
и
 о
...о
о
...о о
о уже определено, то положим •
уже определено, то положим •
![]()
Пользуясь ассоциативностью умножения отображений, нетрудно доказать,что справедливо.
Предложение
3.1.
 ° … °
° … ° °
° °…
°… = (
= ( °...°
°...° )
° (
)
° ( ° …°
° …° )
)
для любого 1 ≤ i < k.
Укажем еще несколько важных свойств композиции отображений.
Теорема 3.2. Пусть f:X→Y, g:Y→Z, h→g о f. Тогда:
1) если f u g инъективны, то и h инъективно;
2) если f u g сюръективны, то и h сюръективно;
3) если f u g биективны, то и h биективно.
Очевидно, третье свойство есть прямое следствие первых двух.
Пусть
f
и g
— инъекции. При любых

 ϵХ,
ϵХ, ≠
≠ f(
f(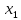 ),
),
f
( )
ϵY
и f
(
)
ϵY
и f
( )
≠f
(х2) в силу инъективности f.
Но тогда g
(f(
)
≠f
(х2) в силу инъективности f.
Но тогда g
(f( ))
≠ =g(f(x2))
из-за инъективности g.
Это доказывает инъективность h,
так как и, следовательно
))
≠ =g(f(x2))
из-за инъективности g.
Это доказывает инъективность h,
так как и, следовательно
 (
( )
≠
)
≠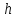 (
( ).
).
Пусть теперь f u g сюръективны. Надо доказать, что и h:X→Z сюръективно, т.е. h(X)=Z. Обозначим буквой z произвольный элемент множества Z. Так как g:Y→ Z сюръективно, то существует хотя бы один элемент yϵY, такой, что g(y) = z. В свою очередь, из сюръективности f:X→Y вытекает существование такого элемента х ϵ X, что f(x) = y. Но тогда h(x)=g (f(x)) =g(y)= z, т. е. h(X) = Z.
Особую
роль при умножении отображений играет
тождественное отображение. Именно: если
f:X→F,
то f
°
 —f
и
—f
и
 °f
= f.
Проверим, например, справедливость
первого равенства. Для любого хϵХ
°f
= f.
Проверим, например, справедливость
первого равенства. Для любого хϵХ
(f° )(x)=f(
)(x)=f( (x))
= f(x),
т. е. f
о
(x))
= f(x),
т. е. f
о
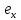 =f.
В случае, когда f
— преобразование множества X,
имеем
=f.
В случае, когда f
— преобразование множества X,
имеем
f
о
 =
= оf
= f.
оf
= f.
Обратное отображение
Пустьf:Х→У
— биективное отображение. Тогда для
любого элемента у ϵ У существует
единственный элемент х ϵ X,
такой, что f(x)=y.
Отображение
 :У→Х,
которое ставит в соответствие каждому
у ϵУ его прообраз х ϵX
при отображении f,
называется обратным к f.
Таким образом, если f
переводит х в у, то
:У→Х,
которое ставит в соответствие каждому
у ϵУ его прообраз х ϵX
при отображении f,
называется обратным к f.
Таким образом, если f
переводит х в у, то
 переводит у в х. Инъективность и
сюръективность отображения
переводит у в х. Инъективность и
сюръективность отображения очевидны,
и, следовательно, для любого биективного
отображения обратное к нему тоже
биективно. При этом
очевидны,
и, следовательно, для любого биективного
отображения обратное к нему тоже
биективно. При этом =f,
т. е. обратное отображение к
=f,
т. е. обратное отображение к
 совпадает
сf.Очевидно,
определены композиции
совпадает
сf.Очевидно,
определены композиции
 °f
и f
o
°f
и f
o
 ,
причем
,
причем
![]()
Действительно,
 o
f:X→X
и для любого х ϵ Х
o
f:X→X
и для любого х ϵ Х
![]()
Аналогично проверяется второе из равенств A. Следующая теорема показывает, что равенства A можно использовать в качестве определения обратного отображения.
Теорема 3.3. Если для отображения f: X→Y существует
отображение
g:Y→X,
такое, что g
о f
=
 иf
о g
=
иf
о g
=
 ,
тоf
биективно и g
=
,
тоf
биективно и g
=
 .
.
Пусть
 ,
, ϵХ
таковы, чтоf(xx)
= f(
ϵХ
таковы, чтоf(xx)
= f( ).
Тогда иg
o
(f(
).
Тогда иg
o
(f( ))
=g
o
(f(
))
=g
o
(f( )),
или
)),
или
g
о f
( )
=g
о f
(
)
=g
о f
( ). (2)
). (2)
Но
go
f
=
 ,
так что из (2) следует
,
так что из (2) следует =
= .
Это доказывает инъективностьf,
так как из
.
Это доказывает инъективностьf,
так как из
 =
= вытекаетf(
вытекаетf( )=f(
)=f( ).
).
Переходя к доказательству сюръективности f, рассмотрим
произвольный элемент у ϵ У:
У
=
 (у) =fog(y)
= f
(g(y)),
(у) =fog(y)
= f
(g(y)),
т. е. у имеет по меньшей мере один прообраз g(y). Итак, f сюръективно, а поэтому и биективно.
Проверим,
наконец, что g
=
 .
Действительно, композиции
.
Действительно, композиции
g°(f
° )
и (g°f)°
)
и (g°f)°
 определены и в силу ассоциативности
умножения отображенийg
° (f
°
определены и в силу ассоциативности
умножения отображенийg
° (f
° = (g
° f)
°
= (g
° f)
°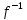 .Но
g°(f °
.Но
g°(f °
 )
= g o
)
= g o = g, a (gof)o
= g, a (gof)o =
= o
o =
=
Итак, мы видим, что обратное отображение к отображению
f:X Y
можно определить, как отображение g:Y→X,
для которого g
о f
=
Y
можно определить, как отображение g:Y→X,
для которого g
о f
= иf
о g
=
иf
о g
= . При этомg
существует тогда и только тогда, когда
f
биективно.
. При этомg
существует тогда и только тогда, когда
f
биективно.
Предложение 3.2. Если f:X→Y и g:Y→Z — биекции, то
 =
=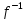 °
° .gof:X→Z.
Так как
.gof:X→Z.
Так как
 :Z→Y,
:Z→Y,
 :Y→X,
то
:Y→X,
то
 o
o
 :
:
:Z→X.
Пусть
хϵХ, f(x)=y,
g(y)=z.
Тогда (gof)(x)
= z,
zϵZ,
( о
о )
(z)
=
)
(z)
=
 (z))
=
(z))
=
 (У) =x.
(У) =x.
Итак,
если g
о f
переводит х в z,
то
 э
э переводитz
в х, т. e.
переводитz
в х, т. e. o
o
 — обратное отображение кg
o
f.
— обратное отображение кg
o
f.
Пусть
f
: Х→ Y
— произвольное отображение. Если у ϵ
F,
то полный прообраз элемента у при
отображении f
обозначается символом
 (у). В случае, когдаf
биективно, символ
(у). В случае, когдаf
биективно, символ имеет уже самостоятельное значение и
имеет уже самостоятельное значение и (у) можно понимать как образ элемента у
при отображении
(у) можно понимать как образ элемента у
при отображении .
Никакой путаницы, однако, по этой причине
не происходит, так как в данном случае
полный прообраз элемента у при отображенииf
состоит из одного элемента
.
Никакой путаницы, однако, по этой причине
не происходит, так как в данном случае
полный прообраз элемента у при отображенииf
состоит из одного элемента
образа
у при отображении

Перестановки и подстановки
В дальнейшем нам понадобятся некоторые дополнительные сведения о подстановках конечных множеств.
Пусть X — конечное множество, состоящее из n элементов. Эти элементы можно перенумеровать с помощью первых n натуральных чисел. Так как природа элементов множества X для нас не важно, то будем считать, что Х = {1, 2, ...,n}. Всякое преобразование f множества X будем записывать так:

Если
f
— подстановка, т. е. биективное
преобразование, то в строке f(1),
f(2),
..., f(n)
выписаны все числа 1, 2, ..., n
без повторений, только, может быть, в
другом порядке. Строки такого вида
называются перестановками из n
чисел. Таким образом, перестановка из
n
чисел — это расположение чисел 1, 2, ...,
n
в некотором определенном порядке. Две
перестановки из n
чисел различаются порядком элементов,
но не элементами. Итак, если f
— подстановка множества X, то нижняя
строка (1) есть некоторая перестановке
из n
чисел. Обратно, если

 ,
...,
,
...,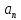 — произвольная перестановка из п чисел,
то преобразование
— произвольная перестановка из п чисел,
то преобразование

множества X является, очевидно, подстановкой. При этом различным перестановкам соответствуют различные подстановки.
Теорема З.4. Количество различных перестановок из n чисел равно n!.
Доказательство проведем индукцией по п. При n = 1 утверждение теоремы очевидно. Будем считать, что n > 1 и число различных перестановок из n—1 чисел равно (n— 1)!.
Разобьем множество всех перестановок из n чисел на классы, состоящие из перестановок с одинаковым последним числом.
Таких классов будет ровно n. Перестановок, лежащих в одном классе с
перестановкой
 ,
, ,
...,
,
..., ,
будет столько, сколько существует
различных перестановок из чисел
,
будет столько, сколько существует
различных перестановок из чисел ,
,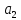 ,
...,
,
..., —и
т. е. (n—1)!!
Так что каждый класс содержит ровно
(n—1)!
перестановок. Но тогда число всех
перестановок из n
чисел равно n(n—1)!
= n
f.
—и
т. е. (n—1)!!
Так что каждый класс содержит ровно
(n—1)!
перестановок. Но тогда число всех
перестановок из n
чисел равно n(n—1)!
= n
f.
Следствие 3.1. Число всех подстановок множества X из n элементов равно n f
Определение 3.4. Пусть

 ,
...,
,
..., (1)
(1)
есть перестановка из n чисел. Подмножество {i,j}(={j, i}) множества {1, 2, ..., n} называется инверсией в перестановке A), если большее из этих двух чисел стоит в перестановке (1) перед меньшим. Если же большее из чисел i, j стоит в (1) после меньшего, то подмножество {i, j} называется порядком в перестановке (1).
Пример 3.16. В перестановке 3, 5, 4, 1, 2 {3, 4}—порядок, а {3, 1} —
инверсия.
Определение 3.5. Перестановка называется четной, если она содержит четное число инверсий. В противном случае перестановку называют нечетной.
Пусть
![]()
и
![]()
есть
две перестановки из n
чисел, а f
— подстановка множества X.
Будем говорить, что подстановка f
переводит перестановку (3) в перестановку
(4), если f(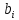 )
=
)
= i=
l,
2, ..., n.
i=
l,
2, ..., n.
Таким
образом, фраза «применить к перестановке
(3) подстановку f»
будет означать «заменить перестановку
(3) перестановкой f( ),f(
),f( ),
...,f
(
),
...,f
( )».
Особый интерес для нас будут представлять
подстановки одного специального вида.
Подстановкаf
множества X
называется транспозицией, если для
некоторой пары чисел i,
jϵX,
i≠j,
f(i)=j,
f(j)
= i,
а всякое другое число из X
f
оставляет на месте. Такую транспозицию
удобно обозначать символом (i,
j)
(не путайте с элементом множества
)».
Особый интерес для нас будут представлять
подстановки одного специального вида.
Подстановкаf
множества X
называется транспозицией, если для
некоторой пары чисел i,
jϵX,
i≠j,
f(i)=j,
f(j)
= i,
а всякое другое число из X
f
оставляет на месте. Такую транспозицию
удобно обозначать символом (i,
j)
(не путайте с элементом множества
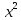 !).
Очевидно, (i,
j)
= (j,
i)
— равенство отображений.
!).
Очевидно, (i,
j)
= (j,
i)
— равенство отображений.
Если транспозицию (i, j) применить к перестановке
…,i ,…,j,…
то, очевидно, получится перестановка где многоточия указывают числа, остающиеся без изменения. Таким образом, после применения к перестановке транспозиции (i, j)
элементы i, j меняются местами.
Теорема 3.5. Если к перестановке один раз применить транспозицию, то характер четности ее изменится на противоположный. Рассмотрим сначала случай, когда транспозиция (i, j) применяется к перестановке в которой числа i, j стоят рядом. В результате получается перестановка
..., i, j, ...,
Число инверсий в перестановке (6) на единицу больше или меньше, чем в (5). Действительно, взаимное расположение чисел i, j с остальными числами, входящими в перестановки(5), (6), не изменилось. В то же время, если {i, j} — инверсия в (5), то {i, j} — порядок в (5), если же {i,j} — порядок в (6), то{i,j} — инверсия в (5).
Пусть теперь транспозиция (i, j) применяется к перестановке
....,i,
 ,…,
,…, ,j,
... (6)
,j,
... (6)
Эта транспозиция переводит (7) в перестановку
...,
j,
 ...,
..., ,i,
... (8)
,i,
... (8)
С
другой стороны, перестановку (8) можно
получить из перестановки (7), применяя
последовательно транспозиции (i,
 ),
(i,
),
(i, ),
..., (i,
),
..., (i,
 ),
(i,
j),
(j,
),
(i,
j),
(j,
 ),
(j,
),
(j,
 ),
..., (j,
),
..., (j,
 ).
Всегоs+
1 + 5 = 2s
+ 1 транспозиций. Так как на каждом шаге
меняются местами соседние числа, то,
согласно уже доказанному, всякий раз
мы теряем или приобретаем точно одну
инверсию, т. е. изменяем характер четности
перестановки на противоположный. Теперь
ясно, что характеры четности перестановок
(7) и (8) различны.
).
Всегоs+
1 + 5 = 2s
+ 1 транспозиций. Так как на каждом шаге
меняются местами соседние числа, то,
согласно уже доказанному, всякий раз
мы теряем или приобретаем точно одну
инверсию, т. е. изменяем характер четности
перестановки на противоположный. Теперь
ясно, что характеры четности перестановок
(7) и (8) различны.
Следствие 3.2. Если n > 1, то количество всех четных перестановок из n чисел равно количеству всех нечетных перестановок из n чисел и, следовательно, равно n!/2. Обозначим буквой а количество всех четных перестановок из n чисел, а буквой b — количество всех нечетных перестановок из n чисел. К каждой из четных перестановок применим одну и т уже транспозицию. Все полученные в результате этого перестановки нечетны и различны, их число равно а. Следовательно, а ≤b
Аналогично доказывается, что b ≤ а. В результате а—b и, так как
различных перестановок из n чисел ровно n!, получаем
а =b = n!/2.
Предложение 3-3. Пусть n > 1. От любой перестановки из n чисел можно перейти к любой другой перестановке из n чисел, последовательно применив несколько подходящих транспозиций.
Пусть
 ,
,
 ,
...,
,
..., (9)
(9)
и
 ,
,
 ,
...,
,
..., (10)
(10)
есть
произвольные перестановки из n
чисел. Если

 то,
применив к перестановке (9) транспозицию
(
то,
применив к перестановке (9) транспозицию
(
 ),
получим перестановку изn
чисел вида
),
получим перестановку изn
чисел вида

 ,
...,
,
...,
 .
(11)
.
(11)
Если
 ≠
≠ ,
то применим к перестановке (11) транспозицию
(
,
то применим к перестановке (11) транспозицию
( ,
, ).
В результате получим перестановку вида
).
В результате получим перестановку вида ,
, ,
, ,
...,
,
..., .
Продолжая этот процесс, получаем
требуемое. Вернемся к изучению подстановок
конечного множества.
.
Продолжая этот процесс, получаем
требуемое. Вернемся к изучению подстановок
конечного множества.
Для любых двух подстановок f u g множества X определено произведение g o f, которое снова есть подстановка X. Договоримся вместо g o f писать в дальнейшем g f.
Так как всякая транспозиция множества X есть подстановка этого множества, то транспозиции можно перемножать. При этом произведение транспозиций есть некоторая подстановка множества X, но, как правило, не транспозиция. Теорема 3-6. Всякую подстановку конечного множества X, содержащего не менее двух элементов, можно представить в виде произведения транспозиций этого множества.
Если е — тождественная подстановка множества X, то
е = (i, j) (i, j), где (i,j) — любая транспозиция X.
Пусть
![]()
есть произвольная нетождественная подстановка X. Рассмотрим перестановки
1, 2,...,n (12)
 ,
,
 ,
...,
,
..., .
(13)
.
(13)
Согласно
предложению 3.3, существует последовательность
транспозиций переводящая перестановку (12) в
перестановку (13). Это означает, что для
любогоi=1,
2,...,n
переводящая перестановку (12) в
перестановку (13). Это означает, что для
любогоi=1,
2,...,n
 ...
...
 (i)
=
(i)
=
Но тогда

т.
е. f
=
Разложение подстановки в произведение транспозиций определено не однозначно. Так, например, к любому такому разложению всегда можно приписать произведение (i, j) (i, j) = е. Однако верна
Теорема 3.7. Характер четности числа сомножителей в разложении подстановки в произведение транспозиций не зависит от выбора разложения.
Пусть
![]()
и
f
= ...
... —
произвольное разложениеf
в произведение транспозиций. Покажем,
что k
имеет тот же характер четности, что и
перестановка
—
произвольное разложениеf
в произведение транспозиций. Покажем,
что k
имеет тот же характер четности, что и
перестановка
 ,
,
 ,
...,
,
..., .
.
В
самом деле, так как f
= ...
... ,
то для любогоt
= 1,2,..., n
,
то для любогоt
= 1,2,..., n
 ...
...
 (i)=
(i)= Это
означает, что последовательность
транспозиций
Это
означает, что последовательность
транспозиций
 переводит перестановку 1, 2, ...,n
в перестановку
переводит перестановку 1, 2, ...,n
в перестановку
 ,
,
 ,
...,
,
..., .
Но перестановка 1, 2, ...,n
четная, а каждое применение транспозиции
меняет характер четности перестановки.
Поэтому число k
является четным тогда и только тогда,
когда перестановка
.
Но перестановка 1, 2, ...,n
четная, а каждое применение транспозиции
меняет характер четности перестановки.
Поэтому число k
является четным тогда и только тогда,
когда перестановка
 ,
,
 ,
...,
,
..., четная. Это доказывает теорему.
четная. Это доказывает теорему.
Определение 3.6. Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, и не четной в противном случае. Из доказательства теоремы 3. 7. следует
Предложение 3.4. Подстановка
![]()
является
четной тогда и только тогда, когда
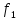 ,
,
 ,
...,
,
..., —четная
перестановка. Следовательно, количество
четных подстановок изn
чисел равно n/12.
—четная
перестановка. Следовательно, количество
четных подстановок изn
чисел равно n/12.
Предложение
35. Подстановки f
и
 имеют один характер четности. Достаточно
проверить, что еслиf
=
имеют один характер четности. Достаточно
проверить, что еслиf
=
 ...
... — произведение транспозиций, то
— произведение транспозиций, то =
= .
.
В заключение сделаем одно полезное замечание. Подстановку
![]()
иногда удобно записывать в виде

 ,
,
 ,
...,
,
..., — некоторая перестановка из п чисел.
Так, если
— некоторая перестановка из п чисел.
Так, если
![]()
то
![]()
При необходимости всегда можно перейти от записи (14) к обычной записи.
Список литературы
Милованов М. В. и др. Алгебра и аналитическая геометрия: [Учеб. Пособие для мат. спец. ун-тов и пед. ин-тов]/М. В. Милованов, Р. И. Тышкевич, А. С. Феденко.— Мн.: Выш. шк., 1984.—302 с, ил.
Александров П. С. Курс аналитической геометрии и линейной алгебры.—М: Наука, 1979.—512 с.
Бурдун А. А., Мурашко Е. А., Феденко А. С. Сборник задач по алгебре и геометрии.— Мн.: Изд-во БГУ, 1979.— 200 с.
Ильин В. А., Позняк Э. Г. Аналитическая геометрия.— М.Наука, 1982. 232с.
Кострикин А. И. Введение в алгебру.— М.: Наука, 1977.— 496с.
Моденов 77. С, Пархоменко А. С. Сборник задач по аналитической
геометрии.— М.: Наука, 1976.— 384 с.
Постников М. М. Аналитическая геометрия.— М.: Наука, 1979.— 336 с.
Фаддеев Д. /С, Соминский Н. С. Сборник задач по высшей алгебре.— М.: Наука, 1977.—288 с.
