
ДЛЯ ПОДГОТОВКИ К С2 - ЕГЭ-2014
.pdfПРИМЕНЕНИЕ ТЕОРЕМЫ О ПЛОЩАДИ ОРТОГОНАЛЬНОЙ ПРОЕКЦИИ МНОГОУГОЛЬНИКА ПРИ РЕШЕНИИ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ
Бардушкин В.В., Белов А.И., Ланцева И.А., Прокофьев А.А., Фадеичева Т.П.
Существует несколько методов решения стереометрических задач на вычисление площадей сечений, поверхностей многогранников и углов (между плоскостями, между прямой и плоскостью и т.д.). Эти методы достаточно подробно рассмотрены в школьных учебниках, изложены в различных пособиях по стереометрии. Так, например, при вычислении площадей широко применяется подход, основанный на разбиении многоугольника на части (на треугольники и четырёхугольники). Если в каждой из частей удаётся вычислить длины сторон (или диагоналей четырёхугольника) и какие-нибудь углы, то можно по известным формулам найти их площади, а значит, решить задачу. Довольно большое значение придаётся векторно-координатному методу решения подобных задач. Однако, на наш взгляд, многие из авторов-составителей не уделяют должного внимания методу вычисления площадей и углов, связанному с ортогональным проектированием многоугольника на некоторую плоскость. Накопленный нами опыт преподавания стереометрии, частично отражённый в настоящей статье, показывает, что изучение такой темы как «Площадь ортогональной проекции многоугольника» повышает у школьников интерес к предмету, стимулирует освоение ими других серьёзных тем по геометрии, что в итоге ведёт к интенсификации всего процесса обучения.
1. Теорема о площади ортогональной проекции плоской фигуры
Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций, называется ортогональным.
Ортогональной проекцией фигуры на данную плоскость называют множество точек пересечений с этой плоскостью перпендикулярных к ней прямых, проходящих через все точки этой фигуры. В общем случае справедлива следующая теорема.
Если фигура Ф с площадью SФ лежит в плоскости , а фигура Ф с площадью SФ является ортогональной проекцией фигуры Ф на плоскость , то имеет место равенство
SФ SФ cos ,
где – угол между плоскостями и .
В школьном курсе стереометрии приведённая теорема формулируется и доказывается лишь для случая, когда проектируемая фигура – плоский многоугольник. В этом случае формулировка имеет вид:
Площадь Sпр ортогональной проекции многоугольника на плоскость равна произве-
дению его площади Sмн , умноженной на косинус угла между плоскостью много-
угольника и плоскостью проекции: Sпр Sмн cos .
2. Применение теоремы о площади ортогональной проекции многоугольника при нахождении площадей сечений
Эту теорему с успехом применяют, прежде всего, при вычислении площадей сечений многогранников. Данный подход используется в ситуациях, когда нахождение площади Sпр ортогональной проекции многоугольника, полученного в сечении, и угла между
секущей плоскостью и плоскостью проектирования сопряжено с меньшими трудностями, чем непосредственное вычисление площади сечения. В этом случае
Sсечения |
|
S |
пр |
. |
(1) |
|
cos |
||||||
|
|
|
|
|||
1
В примерах 1 – 4 иллюстрируется это основное применение теоремы о площади ортогональной проекции многоугольника.
|
B1 |
|
C1 |
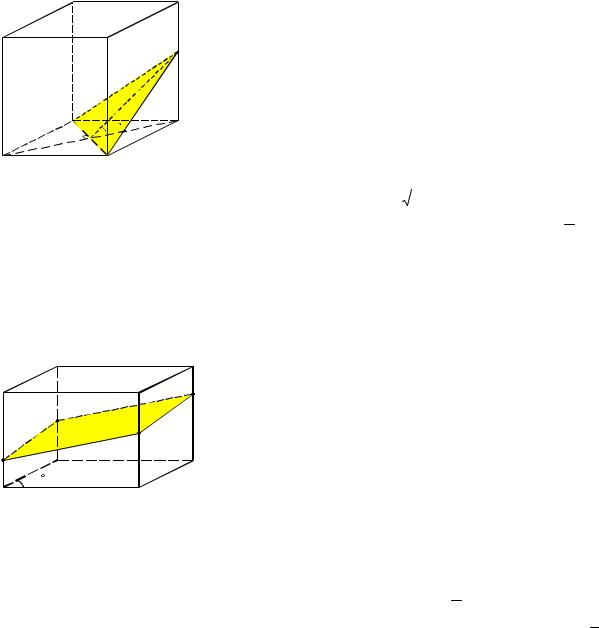
Пример 1. В правильной четырёхугольной призме |
|||||||
|
|
|
|
сторона основания равна 4 см. Через диагональ основа- |
|||||||
A1 |
|
D1 |
|
ния под углом 45 |
к плоскости основания проведена |
||||||
|
|
M |
плоскость, пересекающая боковое ребро. Найти пло- |
||||||||
|
|
|
|||||||||
|
|
|
|
щадь сечения. |
|
|
|
|
|||
|
|
|
|
Решение. Согласно условию задачи, площадь ор- |
|||||||
|
B |
|
|
тогональной проекции сечения на плоскость основания |
|||||||
|
45 |
C |
призмы равна половине его площади (см. рис. 1), т.е. |
||||||||
|
|
||||||||||
|
O |
|
|
42 |
8 (см2). Тогда, используя формулу (1), полу- |
||||||
A |
D |
|
Sпр |
|
|||||||
|
2 |
||||||||||
|
|
|
|
чаем: Sсечения |
Sпр |
|
|
2 |
|||
|
|
|
|
|
|||||||
|
Рис. 1 |
|
|
|
8 2 (см ). |
||||||
|
|
|
|
||||||||
cos45
Ответ: 8
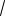 2 см2.
2 см2.
Пример 2. Стороны основания прямого параллелепипеда равны 4 и 5, угол между ними равен 30°. Найти площадь сечения параллелепипеда плоскостью, пересекающей все его боковые рёбра и образующей с плоскостью основания угол в 45°.
|
Решение. Для нахождения площади сечения воспользуемся формулой (1). Поскольку |
||||||||
|
B1 |
|
|
|
C1 |
секущая плоскость пересекает все боковые рёбра |
|||
|
|
|
|
прямого параллелепипеда ABCDA BC D , то ортого- |
|||||
A1 |
|
D1 |
|
|
1 |
1 |
1 |
1 |
|
|
|
N |
нальной проекцией сечения MQNP является паралле- |
||||||
|
Q |
|
|
|
лограмм ABCD (см. рис. 2). Отметим, что MQNP так- |
||||
|
|
|
|
|
же является параллелограммом, так как MQ||PN и |
||||
|
|
P |
|
|
|||||
M |
|
|
|
MP||QN по свойству параллельных плоскостей (если |
|||||
B |
|
|
|
C |
две параллельные плоскости пересечены третьей, то |
||||
A |
30 |
D |
|
|
линии пересечения параллельны). |
|
|
|
|
|
|
|
Найдем площадь параллелограмма ABCD. Пусть, |
||||||
|
Рис. 2 |
|
|
|
|
для определённости, AB 4, AD 5, |
BAD 30 , |
||
|
|
|
|
|
тогда SABCD AB AD sin BAD 10. |
|
|
||
|
|
|
SABCD |
|
|
|
|||
|
Поскольку SMQNP |
|
, где 45 – угол между плоскостью сечения и основани- |
||||||
|
|
||||||||
|
|
|
|
cos |
|
|
|
|
|
ем параллелепипеда (на рис. 2 этот угол не показан), то SMQNP 10
 2 .
2 .
Ответ: 10
 2 .
2 .
Пример 3. Дан куб ABCDA1B1C1D1 с ребром, равным a. На рёбрах основания AB и AD взяты соответственно точки M и N так, что AM :MB 2:1 и AN :ND 2:1. Найти площадь сечения куба плоскостью, проходящей через точки M, N и C1 .
Решение. Приведём два способа решения этой задачи. Первый способ основан на разбиении многоугольника, полученного в сечении, на части и вычислении по отдельности площадей этих частей, а второй – на использовании теоремы о площади ортогональной проекции многоугольника. Читатель сам сможет определить, какой из предложенных подходов предпочтительнее.
Прежде чем перейти к решению задачи этими двумя способами, используя метод следов, построим сечение куба плоскостью, проходящей через точки M, N и C1. Соединим вначале точки M и N, поскольку они лежат в одной плоскости ABC (см. рис. 3а). Прямая MN лежит в плоскости ABC и пересекает прямые BC и DC в точках P и L соответственно.
2

Точка P принадлежит не только плоскости нижнего основания куба, но и плоскости грани BB1C1 (как и точка C1), поэтому, соединив P и C1, получим на ребре BB1 принадлежащую сечению точку F. Далее, точка L принадлежит не только плоскости нижнего основания куба, но и плоскости грани DD1C1 (как и точка C1), поэтому, соединив L и C1, получим на ребре DD1 принадлежащую сечению точку T. В завершение построения соединим в грани
AA1B1 точки M и F, а в грани AA1D1 точки T и N. Таким образом, сечением куба
ABCDA1B1C1D1 является пятиугольник MFC1TN .
|
|
|
|
|
|
|
B1 |
|
C1 |
|
B1 |
|
|
|
|
A1 |
|
D1 |
|
|
|
C1 |
B1 |
|
|
|
|||
|
|
|
|
C1 |
|
|
|
||
|
|
|
|
|
|
|
|
||
A1 |
D1 |
|
|
|
|
|
|
||
A1 |
|
D1 |
|
F |
|
|
|||
|
|
|
|
|
|
|
|||
|
F |
|
|
|
|
M |
B |
|
C |
P |
|
|
F |
|
|
T |
|||
B |
|
|
|
||||||
|
|
B |
|
O |
|
D |
|
||
M |
T |
|
C |
T |
A |
N |
|
||
|
|
|
M |
|
C |
|
|
|
|
A |
N |
D |
A |
O |
D |
A2 |
|
|
|
|
L |
|
N |
|
|
|
|||
|
а |
|
|
|
б |
|
в |
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
Первый способ решения. Проведём в пятиугольнике MFC1TN диагональ FT. Она ра-
зобьёт сечение на треугольник FC1T и четырёхугольник MFTN. Вычислим их площади по отдельности.
Найдем вначале площадь четырёхугольника MFTN. Поскольку MN || BD и BD лежит в плоскости BB1D1 , то MN || BB1D1 (по признаку параллельности прямой и плоскости). Так как секущая плоскость проходит через MN и пересекает плоскость BB1D1 по прямой TF, то TF ||MN (по теореме о линии пересечения). Далее, поскольку BD||MN и TF ||MN , то TF || BD. Следовательно, четырёхугольник MFTN – трапеция.
Из |
прямоугольного треугольника AMN по теореме Пифагора находим |
||||||
|
|
|
2a |
|
|
. Поскольку BF || DT , как отрезки, расположенные на боко- |
|
|
|
2 |
|||||
MN |
AM2 AN2 |
||||||
|
|
|
|||||
|
|
3 |
|
|
|
||
вых рёбрах куба, то четырёхугольник BFTD – параллелограмм, а значит, TF BD a
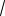 2 . Покажем, что трапеция MFTN – равнобедренная. Для этого рассмотрим вначале пря-
2 . Покажем, что трапеция MFTN – равнобедренная. Для этого рассмотрим вначале пря-
моугольный треугольник LDN. В нём ND a , LND 45 , следовательно, LD a . Да-
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
||||||
лее, треугольники LDT и |
LCC |
|
подобны |
с коэффициентом k |
LD |
|
1 |
. Поэтому |
||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
LC 4 |
||||||
|
CC1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
DT |
|
a |
. Так как четырёхугольник BFTD – параллелограмм, то BF DT |
a |
, а зна- |
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
||||||||||||||||||
4 |
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||||
чит, прямоугольные треугольники NDT и MBF равны по двум катетам. Поэтому, по тео- |
||||||||||||||||||||
реме Пифагора, NT MF |
a |
2 |
|
a |
2 |
|
5a |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||
|
|
12 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|||
3

Далее находим длину h1 высоты этой равнобедренной трапеции MFTN. Опуская очевидные выкладки (читателю предлагается проделать их самостоятельно), получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
a 17 |
|
. Отсюда S |
MFTN |
|
TF MN |
h |
a 2 2a 2 3 |
|
a 17 |
|
|
5a2 34 |
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
12 |
|
2 |
2 |
|
|
|
12 |
|
72 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Решим теперь задачу вычисления площади треугольника FC1T . Найдём в нём длины |
|||||||||||||||||||||||||||||||||
сторон FC1 и TC1 . Для этого рассмотрим прямоугольные треугольники FB1C1 |
и TD1C1. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Они равны по двум катетам, поэтому по теореме Пифагора FC1 TC1 a |
2 |
3a |
2 |
|
5a |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||
|
|
|
4 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||
т.е. треугольник FC1T – равнобедренный. Найдем длину h2 высоты этого треугольника. Опуская очевидные выкладки (читателю предлагается проделать их самостоятельно), по-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 17 |
|
|
|
|
|
|
|
|
|
|
|
TF h |
|
|
|
|
1 |
|
|
|
|
|
a |
17 |
|
|
a2 34 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
лучим h |
|
|
|
|
. Отсюда S |
FC T |
|
|
|
2 |
|
|
|
|
a |
|
2 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 |
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
8 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Наконец, площадь всего сечения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
5a2 |
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
7a2 |
|
|
|
|
|
|
|
|
|
|
7a2 |
|
|
|
||||||
SMFC TN SMFTN |
S FC T |
|
|
34 |
|
|
|
34 |
|
|
|
|
34 |
|
. |
|
|
|
|
|
|
Ответ: |
34 |
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
1 |
|
|
72 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Второй способ решения. Для нахождения площади сечения воспользуемся формулой (1). Ортогональной проекцией пятиугольника MFC1TN на плоскость ABC служит многоугольник MBCDN (см. рис. 3б). Найдём площадь MFC1TN . Очевидно, что SMBCDN SABCD S AMN . Треугольник AMN – прямоугольный. Длины его катетов AM и
AN, согласно условию задачи, равны |
2a |
. Поэтому SMBCDN a |
2 |
|
1 |
2a |
2 |
|
7a2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||
3 |
|
|
|
|
9 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|||||
Далее, проведём в квадрате ABCD диагонали BD и AC. Равнобедренные прямоуголь- |
|||||||||||||||||||||||||||||
ные |
треугольники |
AMN |
и |
ABD |
|
подобны |
с коэффициентом |
|
k |
2 |
. Тогда |
||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
AO |
2 |
|
AC |
|
AC |
, |
OC AC AO |
2a |
|
2 |
|
. Кроме того, поскольку MN || BD и BD AC , |
|||||||||||||||||
3 |
2 |
3 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то MN OC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Соединим точки O и C1. Тогда OC1 |
|
– наклонная к плоскости ABC, OC – проекция на- |
|||||||||||||||||||||||||||
клонной |
OC1 |
и MN OC. |
Следовательно, по |
теореме |
|
о |
|
трёх |
перпендикулярах, |
||||||||||||||||||||
MN OC1 . Значит, |
COC1 |
– линейный угол двугранного угла CMNC1 . |
|
|
|
|
|
||||||||||||||||||||||
Вычислим теперь косинус угла между плоскостью сечения и нижним основанием куба. Для этого рассмотрим прямоугольный треугольник CC1O . По теореме Пифагора
|
|
|
a 17 |
. Откуда cos |
OC |
|
2 |
|
2 |
|
. |
|
OC |
OC2 CC2 |
|||||||||||
|
|
|
|
|
|
|||||||
1 |
1 |
3 |
|
OC1 |
17 |
|
|
|||||
|
|
|
|
|
||||||||
Поскольку, согласно теореме о площади ортогональной проекции многоугольника,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SMFC TN |
S |
MBCDN |
, то окончательно получим: SMFC TN |
7a |
2 |
|
|
17 |
|
|
7a2 34 |
||||
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
cos |
|
|
|
|
|
|
|
|||||||
1 |
|
1 |
9 |
|
|
2 2 |
|
|
36 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
Замечание. При решении задачи вторым способом для нахождения cos можно до-
строить секущую плоскость до её пересечения с продолжением ребра AA1 за точку A (см.
рис. 3в). Тогда cos |
SA BC D |
||
|
1 1 1 1 |
. |
|
|
|
||
|
SA MFC TN |
||
2 |
1 |
|
|
4
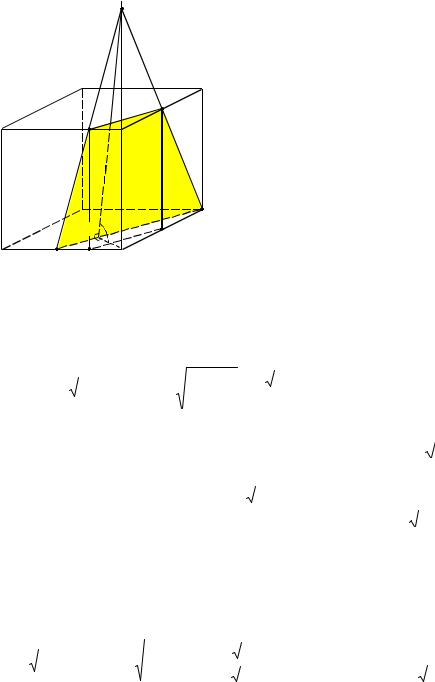
Пример 4. Дан куб ABCDA1B1C1D1 с ребром, равным a. Точка M – середина ребра AD,
точка N – середина ребра C1D1 . Найти площадь сечения куба плоскостью, проходящей через точки M, N и C.
Решение. Построим сечение куба плоскостью, проходящей через точки M, N и C. Соединим вначале точки M и C, поскольку они лежат в одной плоскости ABC. Затем соединим точки C и N, так как они лежат в одной плоскости DD1C1 (см. рис. 4). Прямые СN и
DD1 лежат в плоскости DD1C1 |
и не параллельны. Значит, они пересекаются в точке Q. |
||||
Точка Q принадлежит не только плоскости DD1C1, но и плоскости грани AA1D1 (как и |
|||||
точка M), |
поэтому, |
соединив M и Q, получим на ребре A1D1 принадлежащую сечению |
|||
точку P. В завершение построения соединим в верхней грани куба точки P и N. |
|||||
|
|
|
Q |
Отметим, что плоскости оснований куба парал- |
|
|
|
|
лельны друг другу. Значит, по свойству параллель- |
||
|
|
|
|
ных плоскостей (если две параллельные плоскости |
|
|
|
|
|
пересечены третьей, то линии пересечения парал- |
|
|
|
B1 |
C1 |
лельны) MC|| PN . Далее, поскольку прямые MP и |
|
|
|
CN пересекаются в точке Q, то стороны MP и CN че- |
|||
A1 |
|
P |
N |
тырёхугольника MPNC не параллельны. Таким обра- |
|
|
D1 |
зом, сечением куба ABCDA1B1C1D1 является трапеция |
|||
|
|
|
|||
|
|
|
MPNC. |
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения площади сечения воспользуемся |
|
|
|
|
|
формулой (1). Построим вначале линейный угол дву- |
|
|
|
BO |
C |
гранного угла DMCQ. Для этого в прямоугольном |
|
|
|
треугольнике MCD опустим перпендикуляр DO к ги- |
|||
|
|
|
N1 |
потенузе MC. Соединим точки O и Q. Тогда QO – на- |
|
A |
M |
P1 D |
клонная к плоскости ABC, DO – проекция наклонной |
||
|
|
|
|
QO и MC DO. |
Следовательно, по теореме о трёх |
|
|
Рис. 4 |
|
перпендикулярах, |
MC QO. Значит, QOD – |
|
|
|
|
линейный угол двугранного угла DMCQ. |
|
Вычислим теперь косинус угла между плоскостью сечения и нижним основанием куба. Для этого рассмотрим вначале прямоугольный треугольник MCD. По теореме Пифа-
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
a 5 |
. Для нахождения высоты DO выразим пло- |
|||||||||||||||||||
гора MC |
|
MD2 DC2 |
a2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
щадь S MCD |
двумя способами: |
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
MD DC |
|
a2 |
|
|
|
|
|
MC DO |
|
|
a |
|
|
|
|||||||||||
|
|
S MCD |
|
|
|
, S MCD |
|
5 |
|
DO. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
a2 |
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
||||||||||
|
|
|
|
|
5 |
DO. Отсюда DO |
|
|
|
||||||||||||||||||||
Тогда, приравняв их, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||
4 |
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
5 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Далее, рассмотрим прямоугольные треугольники CDQ и ND1Q. У этих треугольников острый угол при вершине Q – общий. Значит, они подобны. Поскольку, согласно условию
задачи, точка N – |
середина ребра C1D1, то коэффициент подобия треугольников CDQ и |
||||||||||||||||||||||
ND1Q равен 2. Отсюда, очевидно, что DQ 2a. |
|
|
|
|
|
|
|||||||||||||||||
Рассмотрим, |
наконец, |
|
прямоугольный треугольник QOD. По теореме Пифагора |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a2 |
|
a |
|
|
|
|
DO |
|
1 |
|
|
|||
|
|
|
|
|
|
|
2 |
|
21 |
|
|
||||||||||||
QO DQ |
2 |
DO |
2 |
4a |
|
. Откуда cos |
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
5 |
|
|
|
|
|
|
QO |
|
|
|
||||||||||
|
|
|
|
5 |
|
|
21 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Построим теперь четырёхугольник MP1N1C, являющийся ортогональной проекцией трапеции MPNC на плоскость ABC. Так как PN лежит в плоскости, построенной на парал-
5
лельных прямых PP1 и NN1, |
и параллельна плоскости ABC, |
|
то линия пересечения |
P1N1 |
|||||||||||||||||||||||||||
плоскостей ABC и PNN1 |
параллельна PN (по теореме о линии пересечения). Поскольку |
||||||||||||||||||||||||||||||
P1N1 || PN и MC|| PN , то P1N1 ||MC, а значит, четырёхугольник MP1N1C – трапеция. |
|
|
|
|
|||||||||||||||||||||||||||
Найдём площадь трапеции MP1N1C. Очевидно, что SMPN C S |
MCD |
S PN D . Прямо- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
||
угольные треугольники MCD и P1N1D подобны, так как P1N1D MCD (как соответст- |
|||||||||||||||||||||||||||||||
венные). Точка |
N1 – середина ребра CD, значит, |
коэффициент подобия треугольников |
|||||||||||||||||||||||||||||
MCD и PN |
D равен 2. Поэтому S |
MPN C |
S |
MCD |
|
S |
MCD |
|
a2 |
|
a2 |
|
|
3a2 |
. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 1 |
|
|
|
|
|
|
|
4 |
|
|
4 |
|
16 |
|
16 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Согласно |
теореме |
о |
площади |
ортогональной |
проекции |
многоугольника, |
|||||||||||||||||||||||||
|
SMP1N1C |
|
|
|
|
|
|
|
|
|
|
|
3a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
SMPNC |
, откуда окончательно получим: SMPNC |
21 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
cos |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
21 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
16
3. Применение теоремы о площади ортогональной проекции многоугольника при вычислении угла между плоскостями
Кроме рассмотренного основного применения теоремы о площади ортогональной проекции многоугольника её можно также использовать при вычислении угла между плоскостью сечения и плоскостью какой-либо грани многогранника (обычно в качестве такой грани выступает основание пирамиды или призмы). Так поступают в случаях, когда нахождение Sпр и Sсечения является более простой задачей, чем непосредственное вычисление двугранного угла , сопряжённое с построением на чертеже его линейного угла.
B1
A1 D1
D1
B
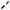
A D
Рис. 5
Из формулы о
C1 |
Пример 5. В кубе |
ABCDA1B1C1D1 найти угол между |
||||||||||||
|
плоскостью грани AA1B1B и плоскостью BC1D. |
|
||||||||||||
|
Решение. Пусть ребро куба равно a. Ортогональной |
|||||||||||||
|
проекцией треугольника BC1D является треугольник AB1B |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
||
C |
(см. рис. 5), площадь |
которого равна |
|
|
. |
Поскольку |
||||||||
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
BD BC1 |
C1A a |
|
|
(как диагонали |
граней |
куба), то |
|||||||
|
2 |
|||||||||||||
|
|
|
|
|
|
a2 . |
|
|
|
|
|
|||
|
S BC D |
|
|
3 |
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
площади ортогональной проекции многоугольника получим:
cos
A1
A
S AB B |
|
|
3 |
|
. Отсюда arccos |
|
3 |
|
. |
Ответ: arccos |
|
3 |
|
. |
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
S BC D |
3 |
|
3 |
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
P |
|
C1 |
Пример 6. В кубе |
ABCDA1B1C1D1 через его вершины |
||||||||
|
|
|
|
|
|
|
A , D и точку M, расположенную на ребре CC |
так, что |
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
D1 |
|
M |
CM :MC1 2:1, проведено сечение. Найти угол наклона |
|||||||||||
Q |
|
|
|
|
|
секущей плоскости к плоскости основания ABCD. |
|
|
|
|
|||||||||
|
K |
|
|
|
|
|
|
|
Решение. Построим сечение куба плоскостью, прохо- |
||||||||||
B |
|
|
|
|
|
L |
C |
дящей через точки A1, D и M. Соединим вначале точки A1 |
|||||||||||
|
|
|
|
|
|
|
|
|
и D, поскольку они лежат в одной плоскости DD A . Затем |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
Dсоединим точки D и M, так как они лежат в одной плоскости DD1C1 (см. рис. 6). Противоположные боковые грани
Рис. 6 |
DD1A1 |
и CC1B1 в кубе параллельны. Поэтому секущая |
|
6

плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии пересечения параллельны) будет пересекать грань CC1B1 по прямой MP так, что MP|| A1D . Наконец, соединим точки A1 и P, так как они лежат в одной плоскости A1B1C1. Поскольку A1P и DM не параллельны, то четырёхуголь-
ник A1PMD, являющийся сечением куба, – трапеция.
Ортогональной проекцией трапеции A1PMD плоскости основания ABCD является прямоугольная трапеция ALCD. Для определения угла наклона секущей плоскости к
плоскости основания ABCD воспользуемся формулой cos SALCD . Для этого найдем
SA1PMD
площади указанных трапеций.
Пусть ребро куба равно a. Тогда, согласно условию задачи, MC a . Кроме того, |
|
1 |
3 |
очевидно, что A1D a
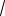 2. Поскольку MP|| A1D и DD1 ||MC1, то A1DD1 PMC1 (как углы с соответственно сонаправленными сторонами). Поэтому прямоугольные треуголь-
2. Поскольку MP|| A1D и DD1 ||MC1, то A1DD1 PMC1 (как углы с соответственно сонаправленными сторонами). Поэтому прямоугольные треуголь-
ники A DD и PMC подобны с коэффициентом k |
1 |
. Следовательно, MP |
A1D |
|
a 2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|||||||||||||||
|
A1D1 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
и PC |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Далее, |
так как |
A B DC a, B P CM |
|
, |
|
|
|
то |
|
прямоугольные |
треугольники |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A1B1P |
|
|
DCM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и |
|
равны |
|
|
|
по |
|
|
двум |
|
катетам. |
|
Поэтому |
|
|
по |
|
|
теореме |
|
|
Пифагора |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
4a2 |
|
|
|
a |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A P DM a2 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, трапеция A1PMD равнобедренная. Найдём её высоту. Для этого опус- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тим из |
точек P |
и |
|
|
|
M |
|
перпендикуляры |
|
PQ и |
|
|
|
|
MK |
|
|
на |
|
|
|
основание A1D. Тогда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A1D MP |
|
|
a |
|
|
. Отсюда по теореме Пифагора из прямоугольного треуголь- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
AQ DK |
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13a2 |
|
2a2 |
|
|
a |
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|||||||||||||||||
ника A PQ высота трапеции A PMD равна: |
PQ |
|
|
|
|
A P2 |
|
AQ2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
9 |
|
|
9 |
|
|
3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A D MP |
|
|
|
|
|
|
|
|
|
2a2 |
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Таким образом, площадь сечения: SAPMD |
|
1 |
|
|
|
|
|
|
PQ |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В прямоугольной трапеции ALCD основания равны AD a |
и LC PC |
, |
|
а высота |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AD LC |
|
|
|
|
2a2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
DC a . Тогда её площадь: |
|
SALCD |
DC |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставляя полученные значения площадей в формулу, находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
2a |
2 |
|
2a2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
ALCD |
|
: |
22 |
|
22 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SAPMD |
3 |
|
9 |
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arccos |
3 |
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||
Следовательно, arccos |
22 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
||||||||||||
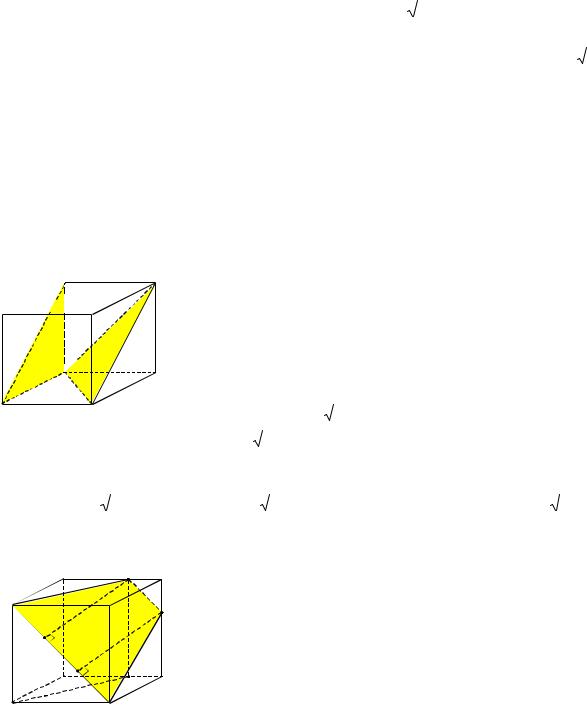
Пример 7. Плоскость пересекает прямоугольный параллелепипед с квадратным основанием по ромбу с острым углом . Под каким углом эта плоскость пересекает боковые рёбра параллелепипеда?
7
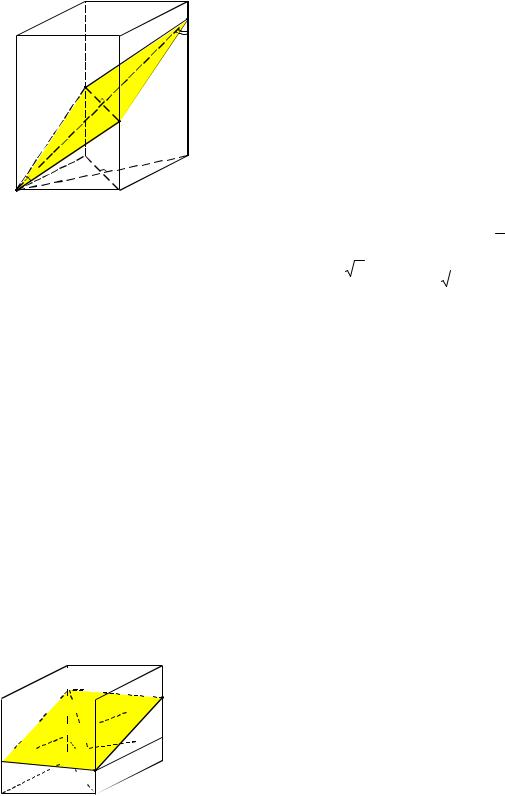
Решение. Без ограничения общности рассуждений будем считать, что секущая плоскость проходит через вершину A нижнего основания параллелепипеда, пересекая его бо-
ковые рёбра BB1, CC1 |
и DD1 |
в точках M, N и P соответственно (см. рис. 7). |
|||
|
B1 |
|
C1 |
Рассмотрим прямоугольные треугольники AMB и |
|
|
|
D1 |
|
N |
APD. В них AM AP , т.к., согласно условию, AMNP – |
A1 |
|
|
ромб. Кроме того, AB AD как стороны основания |
||
|
|
x |
|
параллелепипеда ABCD, являющегося квадратом. Сле- |
|
|
|
|
|
||
|
|
|
x |
|
довательно, AMB APD по гипотенузе и катету, а |
|
M |
|
|
значит, MB PD. |
|
|
|
O |
|
|
Рассмотрим теперь четырёхугольник BMPD. В нём |
x |
|
P |
|
|
противоположные стороны MB и PD параллельны и |
|
x B |
a |
|
|
равны, значит, BMPD – параллелограмм (отметим до- |
|
|
C |
полнительно, что BMPD – прямоугольник). Отсюда |
||
|
a |
|
a |
MP|| BD и MP BD. |
|
A |
a |
D |
|
|
Пусть сторона ромба AMNP равна x, а ребро осно- |
|
Рис. 7 |
|
|
вания параллелепипеда равно a. Тогда SAMNP x2 sin , |
|
SABCD a2 . Поскольку MP BD a
 2, то из прямо-
2, то из прямо-
угольного треугольника AOP имеем: sin |
|
|
OP |
|
a 2 |
, или a x |
|
|
sin |
|
. |
|
|
|
||||||||||||||||||
|
2 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
AP |
|
2x |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
Вычислим косинус угла между секущей плоскостью и основанием: |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
SABCD |
|
|
|
|
a2 |
|
|
|
2x2 sin2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
cos |
|
|
|
|
|
|
2 |
|
tg |
. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
SAMNP |
|
|
|
|
|
|
x2 sin |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Обозначим через угол, |
|
|
|
|
x2 sin |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
под которым секущая плоскость пересекает боковые рёбра |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
параллелепипеда. Поскольку |
|
|
|
|
, то |
cos cos |
|
|
sin . Значит, |
sin tg |
|
. |
||||||||||||||||||||
2 |
|
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда arcsin tg |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arcsin tg |
|
. |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
Пример 8. В кубе ABCDA1B1C1D1 с ребром, равным a, через точки M, P и N на рёбрах |
|||||||||
BB , CC и DD соответственно, такие, что BM |
3a |
, CP |
2a |
и DN |
a |
, проведена се- |
||||
1 |
1 |
1 |
4 |
3 |
4 |
|
|
|
||
|
|
|
|
|
|
|||||
кущая плоскость. Найти угол между плоскостью сечения и плоскостью основания куба.
B1 C1
A1  M
M
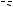




 L
L
 D1
D1 


 P
P 
 K
K



 S
S
Q

 B
B









 C
C
 N
N
A D
Рис. 8
Решение. Построим сечение куба плоскостью, проходящей через точки M, P и N. Соединим вначале точки M и P, поскольку они лежат в одной плоскости BB1C1 . Затем соединим точки P и N, т.к. они лежат в одной плоскости
DD1C1 (см. рис. 8).
Противоположные боковые грани AA1D1 и BB1C1 в кубе параллельны. Поэтому секущая плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии пересечения параллельны) будет пересекать грань AA1D1 по прямой NQ так, что
NQ|| MP.
8

Соединим точки M и Q, т.к. они лежат в одной плоскости AA1B1. Тогда MQ|| NP по
тому же свойству параллельных плоскостей AA1B1 |
и |
|
CC1D1 . Таким образом, |
сечение |
||||||||||||||||||||||||||||||||||||||||||||||||||
представляет собой параллелограмм MPNQ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Вычислим площадь MPNQ и, поскольку квадрат ABCD – ортогональная проекция |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
MPNQ, определим косинус угла между плоскостью сечения и плоскостью ABC. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Найдём стороны треугольника MNP. Используя теорему Пифагора, получим: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
из прямоугольного треугольника MLP (ML CC1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
a2 |
a |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
145 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
MP (LC PC)2 MC2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
144 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
из прямоугольного треугольника NPS (NS CC1) |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
NP |
|
|
|
|
|
|
|
25a2 |
|
a2 |
13a |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
(PC SC)2 NS2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
из прямоугольного треугольника MNK (KN BB1) |
144 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
MN |
|
|
|
|
|
|
|
a2 |
|
2a2 |
3a |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
(BM BK)2 KN2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Полупериметр треугольника MNP равен p |
a( |
|
31) |
. Используя формулу Герона, |
||||||||||||||||||||||||||||||||||||||||||||||||||
145 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
найдём его площадь: |
SMNP |
170 |
|
. Следовательно, |
SMPNQ 2SMNP |
170 |
|
|
. Из фор- |
|||||||||||||||||||||||||||||||||||||||||||||
24 |
|
|
|
12 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SABCD |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
мулы для |
площади |
ортогональной |
|
проекции получим: cos |
|
|
|
|
12 |
|
. Отсюда |
|||||||||||||||||||||||||||||||||||||||||||
|
SMPNQ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
170 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
arccos |
6 |
|
170 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arccos |
6 |
|
170 |
|
. |
|||||||||||||||
|
85 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
85 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. Применениетеоремы о площади ортогональной проекции многоугольника при вычислении площади боковой поверхности пирамиды
Ещё одной известной задачей, при решении которой применяется теорема о площади ортогональной проекции многоугольника, является задача вычисления площади Sбок бо-
ковой поверхности пирамиды, у которой все боковые грани одинаково наклонены к плоскости её основания (под углом ), или вершина пирамиды лежит на перпендикуляре, восставленном из центра вписанной в её основание окружности. Тогда
Sбок |
|
Sосн |
. |
(2) |
|
||||
|
|
cos |
|
|
Пример 9. Стороны основания треугольной пирамиды равны 6 см, 10 см и 14 см. Каждый двугранный угол при её основании равен 30°. Найти площадь боковой поверхности пирамиды.
Решение. Для нахождения площади сечения воспользуемся формулой (2). Найдём вначале площадь основания треугольной пирамиды, воспользовавшись формулой Герона. Поскольку полупериметр треугольника в основании равен 15 см, то
Sосн 
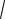 15 (15 6) (15 10) (15 14) 15
15 (15 6) (15 10) (15 14) 15
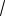 3 (см2).
3 (см2).
Тогда Sбок |
|
Sосн |
|
|
|
3 |
|
2 |
|
|
15 3: |
30 |
|||||||
|
|
(см ). |
|||||||
cos30 |
2 |
||||||||
|
|
|
|
|
|
|
|||
Ответ: 30 см2.
9
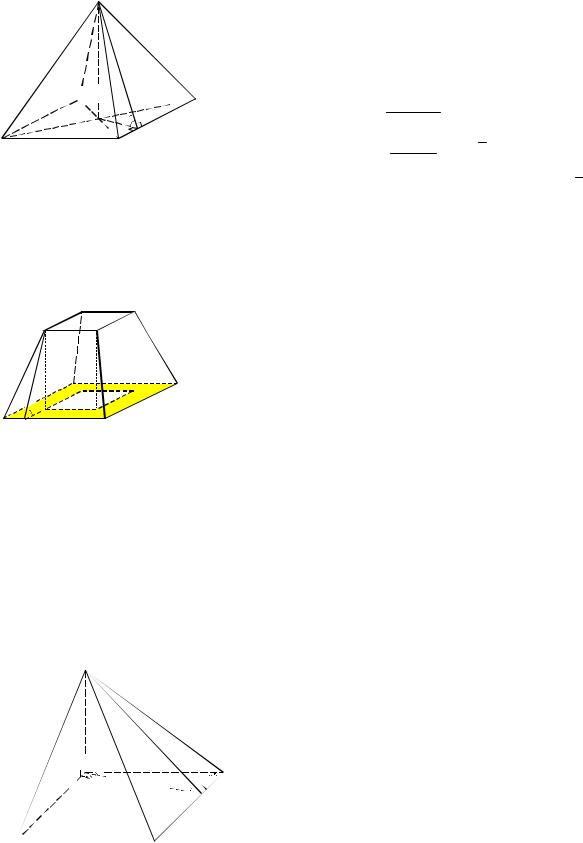
Пример 10. Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30°. Диагонали ромба равны 10 см и 24 см. Найти площадь боковой поверхности пирамиды.
S
B





 C
C
O |
30 |
|
M |
A D
Рис. 9
Решение. Для нахождения площади сечения воспользуемся формулой (2). Поскольку боковые грани пирамиды SABCD наклонены к основанию ABCD под одинаковым углом, то её вершина S проектируется в центр вписанной в ромб окружности, т. е. в точку O пересечения его диагоналей (см. рис. 9). Тогда
SABCD AC BD 120 (см2). 2
Следовательно, Sбок SABCD 80
 3 (см2). cos30
3 (см2). cos30
Ответ: 80
 3 см2.
3 см2.
Пример 11. В правильной усечённой четырёхугольной пирамиде стороны нижнего и верхнего оснований равны соответственно a и b (a b). Найти площадь полной поверхности усечённой пирамиды, если её боковые грани наклонены к плоскости основания под углом .
b |
|
|
|
|
|
Решение. Поскольку основаниями правильной усе- |
|||||||||||
|
|
чённой четырёхугольной пирамиды являются квадраты со |
|||||||||||||||
|
|
|
сторонами a и b, то сумма их площадей равна |
a2 b2 . |
|||||||||||||
|
|
|
Очевидно, что ортогональная проекция боковой поверхно- |
||||||||||||||
|
|
|
сти усечённой пирамиды на плоскость нижнего основания |
||||||||||||||
|
a |
|
представляет собой квадрат со стороной a, из которого |
||||||||||||||
|
«вырезан» квадрат со стороной b. При этом стороны «вы- |
||||||||||||||||
Рис. 10 |
|
|
резанного» квадрата параллельны сторонам нижнего осно- |
||||||||||||||
|
|
вания пирамиды (см. рис. 10). Так как боковые грани усе- |
|||||||||||||||
|
|
|
чённой пирамиды наклонены к плоскости основания под |
||||||||||||||
одинаковым углом , то площадь её боковой поверхности равна: Sбок |
Sпр |
|
a2 |
b2 |
|||||||||||||
|
|
|
|
|
. |
||||||||||||
cos |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|||||
Таким образом, S |
полн a |
2 |
b |
2 |
|
a2 b2 |
Ответ: a |
2 |
b |
2 |
|
a2 b2 |
|||||
|
|
|
. |
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
cos |
|
|
|
|
|
|
cos |
||||
Пример 12. Основанием пирамиды является ромб. Две боковые грани перпендикулярны к плоскости основания и образуют двугранный угол в 120°, а две другие боковые грани наклонены к плоскости основания под углом 30°. Найти площадь поверхности пирамиды, если её высота равна 12.
S
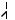
 B
B

 120
120






 30
30
 60
60

 M
M
A  D
D
Рис. 11
Решение. Площадь полной поверхности пирамиды равна сумме площадей боковых граней и основания, т. е.
Sполн SASB SBSC SASD SDSC SABCD .
Положим, что сторона ромба ABCD равна a. C Пусть боковые грани ASB и BSC пирамиды
SABCD перпендикулярны к плоскости основания ABCD (см. рис. 11). Тогда боковое ребро SB пирамиды перпендикулярно к плоскости ромба и равно высоте, а боковые грани ASB и BSC пирамиды являются равными прямоугольными треугольниками
10
