2. Комплексный чертеж прямой и плоскости и их аналитические модели

2.1 Комплексный чертеж прямой

На комплексном чертеже прямая может быть задана проекциями двух ее точек (рис. 2.1) или проекциями отрезка (рис. 2.2).

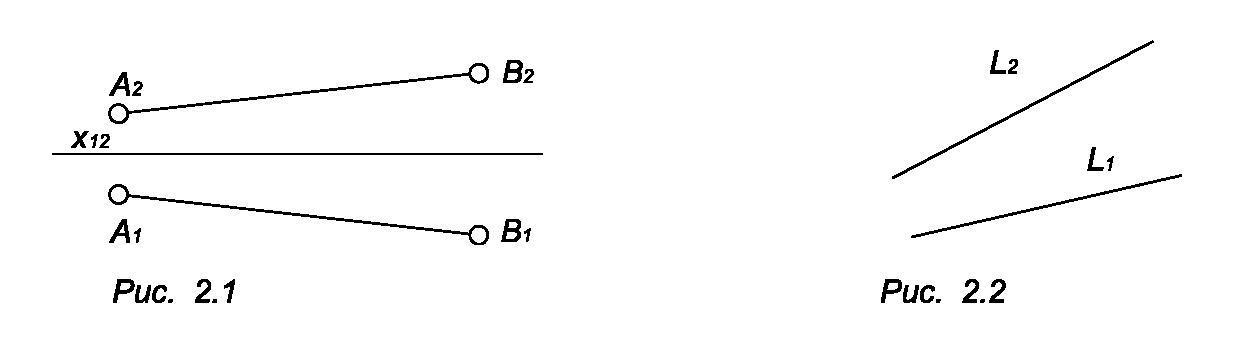
Прямые не параллельны и не перпендикулярны ни одной из плоскостей проекций, называются прямыми общего положения. Прямые общего положения бывают восходящими или нисходящими.

Восходящая прямая по мере удаления от наблюдателя поднимается вверх. Например, прямая L (см. рис. 2.2).

Нисходящая прямая по мере удаления от наблюдателя понижается. Например, прямая АВ (см. рис. 2.1).

Если прямая параллельна или перпендикулярна одной из плоскостей проекций, то она называется прямой частного положения.

Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня (рис. 2.3).

h₁ ║ x₁₂, следовательно, высоты всех точек этой прямой равны между собой и h ║ П₁. Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью.

Отрезок горизонтальной прямой на плоскость П₁ проецируется в натуральную величину. А – угол наклона h к плоскости П₂. f₁ ║ x₁₂, следовательно, глубины всех точек этой прямой равны между собой и f ║ П₂. Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью. Отрезок фронтальной прямой на плоскость П₂ проецируется в натуральную величину. Β – угол наклона f к плоскости П₁ (рис. 2.4). Прямые АВ и СD на рис.2.5 параллельны плоскости П₃ и называются профильными прямыми.

Прямые, перпендикулярные к одной из плоскостей проекций, называются проецирующими прямыми (рис. 2.6).

АВ _┴ П₁, следовательно, на плоскость П₁ АВ проецируется в точку. Прямая АВ называется горизонтально проецирующей. CD _┴ П₂, следовательно, на фронтальную плоскость проекций CD проецируется в точку. Прямая CD называется фронтально проецирующей.

2. Аналитическая модель прямой

И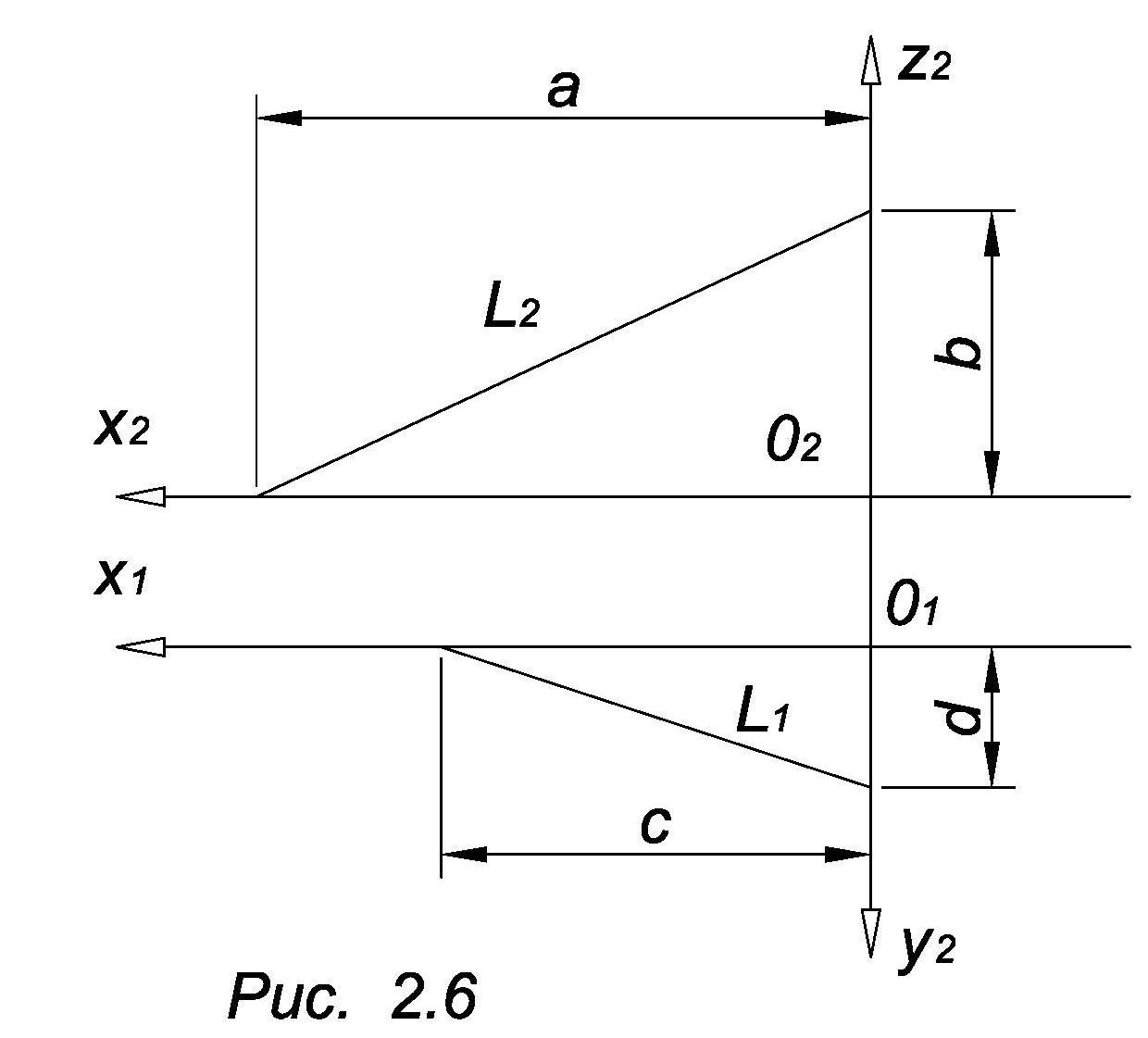звестно, что плоскости прямая может быть задана линейным (первой степени) уравнением с двумя неизвестными. В общем случае это уравнение имеет вид:ax + by + c =0, где x, у – независимые переменные, a, b, с – коэффициенты. Разделив обе части на С, получим уравнение x + у +1 = 0 или а₁x + b₁y + 1 = 0. Линейное уравнение можно задать так же в следующем виде:

+ = 1 или y = kx +m.

На комплексном чертеже пространственная прямая задается двумя проекциями, следовательно, для получения аналитической модели пространственной прямой достаточно задать уравнение ее проекций. Например, прямая L описывается системой из двух линейных уравнений (рис. 2.7):

+ = 1;

Прямая h на рис. 2.3 может быть задана системой уравнений:

z = 0. y = x tg + b.

Прямая CD на рис. 2.6 – системой: x = а, z = c.

2. Взаимное расположение линейных геометрических элементов

Л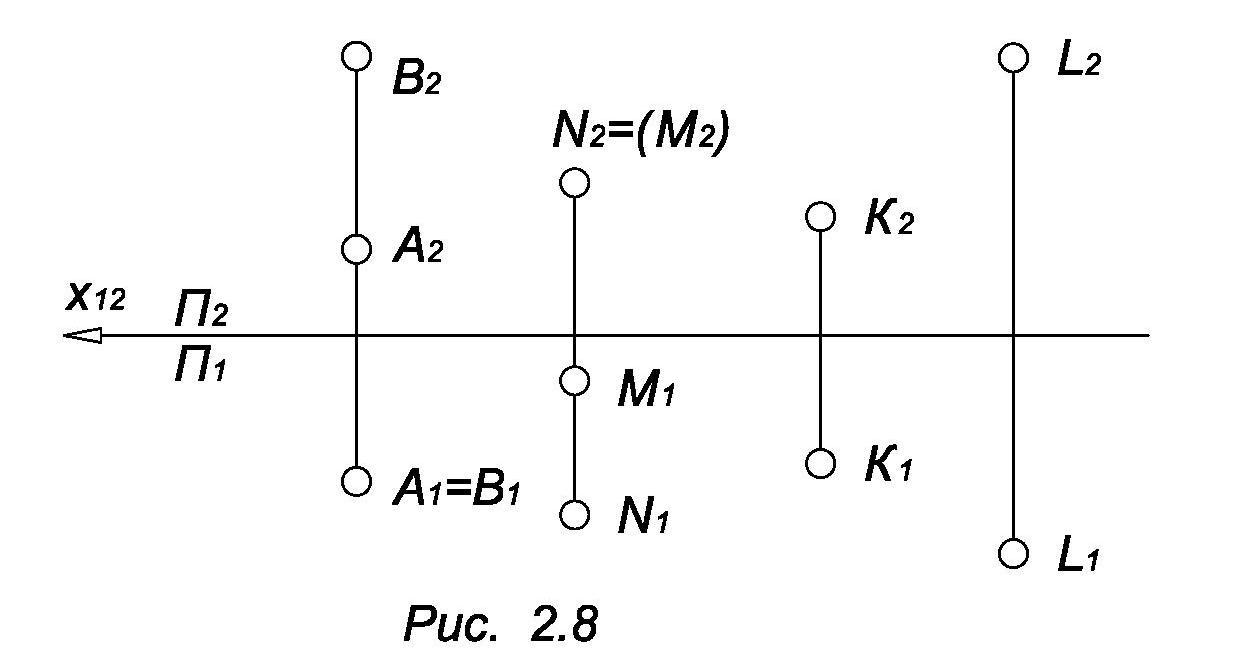инейными геометрическими элементами называются: точка –R⁰, прямая R¹, плоскость – R², трехмерное пространство – R³ и т.д. Взаимное расположение точек рассмотрим на следующем примере. Точки А и В расположены на одном перпендикуляре к горизонтальной плоскости проекций, их горизонтальные проекции совпадают (рис. 2.3). Такие точки называются горизонтально конкурирующими. По чертежу видно, что точка В выше точки А и на горизонтальной проекции точка А – невидимая. Точка М и N расположены на одном перпендикуляре к фронтальной плоскости проекций, поэтому фронтальные проекции этих точек совпадают. Такие точки называются фронтально конкурирующими. Из чертежа видно, что N ближе М, т.е. точка М на фронтальной проекции – невидимая. Про точки К и L можно сказать, что L расположена ближе, выше и правее точки К.

Принадлежность точки и прямой (рис. 2.9) определяются свойством проецирования 3 (Таблица 1.1).

Если прямая задана уравнениями, то значения координат точки, принадлежащей прямой, должны удовлетворять этим уравнениям. Например, точка А (3; 1; 0,75) принадлежит прямой: + = 1, + = 1, т.к. + = 1, + = 1.

Параллельность прямых на чертеже определяется свойством 5 параллельного проецирования (рис. 2.10). Следует учитывать, что в некоторых частных случаях проекции не парралельных прямых могут быть параллельны, например, прямые АВ иCD на рис. 2.5.

Рассмотрим проекции пересекающихся и скрещивающихся прямых (рис. 2.11). Прямые а и b имеют общую точку М, следовательно, они пересекаются. Скрещивающиеся прямые с и d не имеют общих точек. Точки N и K, L и Н, принадлежащие этим прямым, являются конкурирующими.

2. Комплексный чертеж плоскости

Плоскость в пространстве может быть задана: тремя точками, прямой и точкой, двумя параллельными прямыми, двумя пересекающимися прямыми и плоской фигурой. На комплексном чертеже плоскость задается проекциями перечисленных наборов геометрических элементов (рис. 2.12, 2.13, 2.14, 2.15, 2.16).

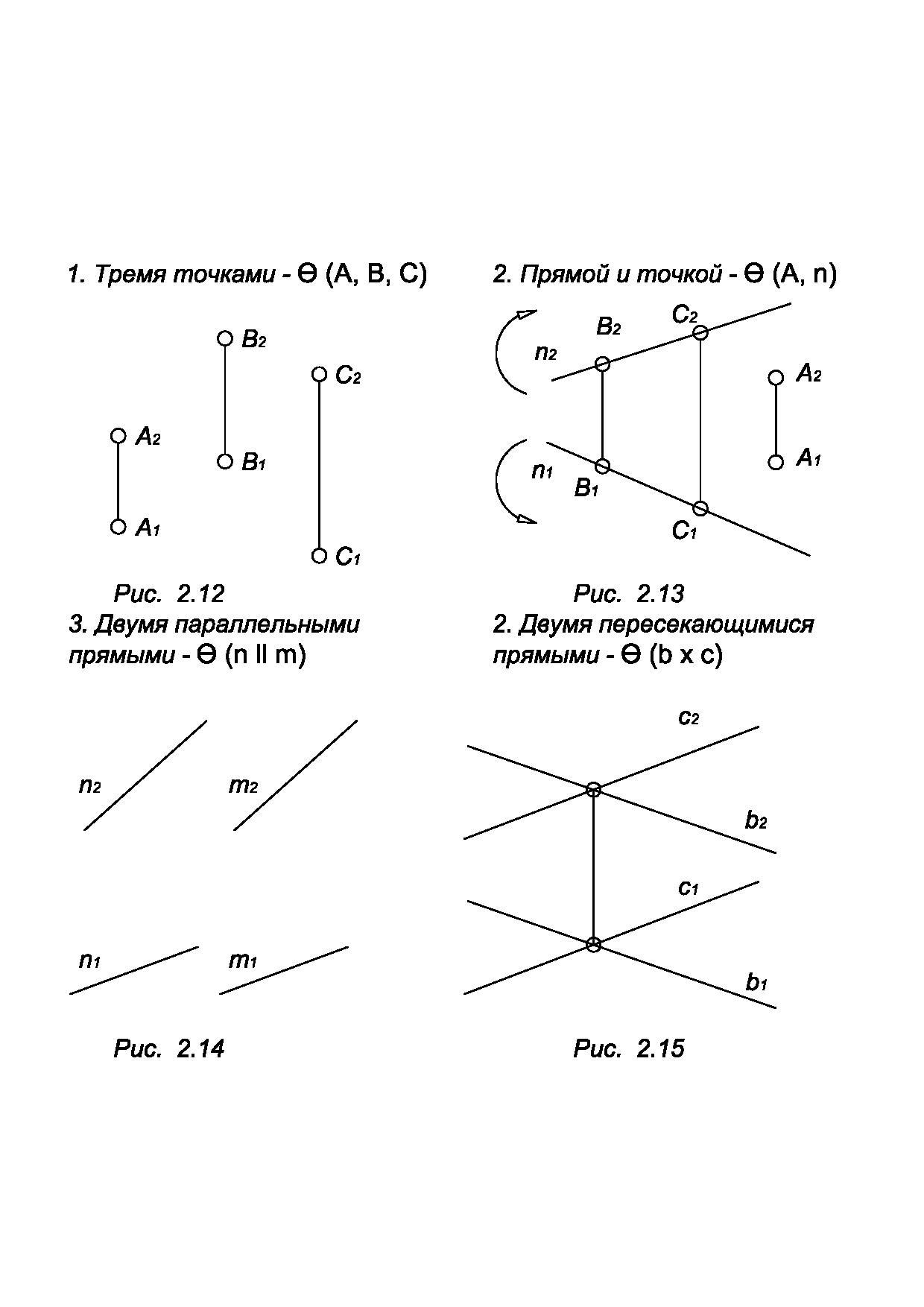
Если не параллельна и не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения. Плоскости общего положения бывают восходящими и нисходящими.

Если плоскость по мере удаления от наблюдателя поднимается вверх, то она называется восходящей. Чтобы избежать недоразумений, удаление надо производить по профильной прямой, принадлежащей плоскости. На комплексном чертеже восходящей плоскости обе проекции треугольника, ей принадлежащего, ориентировано одинаково (рис. 2.16), а для нисходящей – противоположно (рис. 2.13).

Если плоскость параллельна или перпендикулярна одной плоскостей проекций, то она называется плоскостью частного положения. Различают следующие виды плоскостей частного положения:

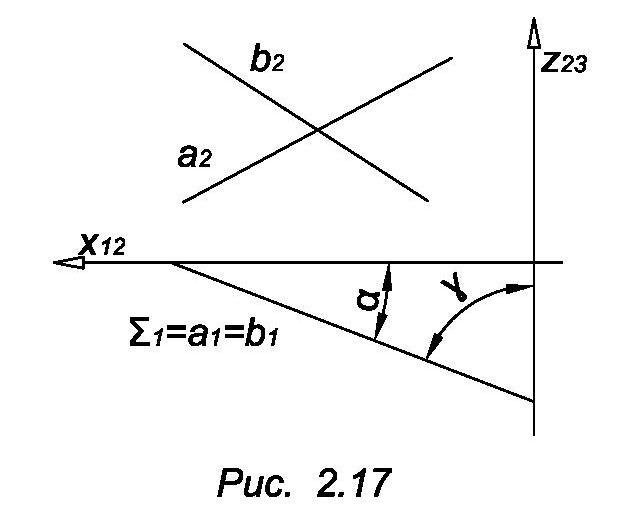1. Плоскость, перпендикулярная к горизонтальной плоскости проекций, называетсягоризонтально проецирующей плоскостью. Все точки и прямые такой плоскости на горизонтальную плоскость проекций проецируются в прямую, например, Z₁ (рис. 2.17) – проекция плоскости 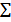, _┴ П₁; а,b € . Фронтальная и профильная проекции ее занимают соответственно все поле проекций П₁ и все поле проекций П₃. Очевидно, что а и ᵞ - углы наклона плоскости , к фронтальной и профильной плоскостям соответственно.

2. Плоскость, перпендикулярная к фронтальной плоскости проекций, называетсяфронтально проецирующей плоскостью, ее фронтальная проекция является прямой, а горизонтальная и профильная проекции занимают соответственно все поле проекций П₁ и все поле проекций П₃ (рис. 2.18). Фронтально проецирующая плоскость Т вполне определяется ее одной проекцией Т₂. Углы β и u измеряют углы наклона плоскости к плоскостям проекций П₁ и П₃ соответственно, А € Т.

3. Плоскость, перпендикулярная к профильной плоскости проекций, называется профильно проецирующей плоскостью, ее профильная проекция является прямой, а горизонтальная и фронтальная проекции занимают соответственно все поле проекций П₁ и все поле проекций П₂ (рис. 2.19). Профильно проецирующая плоскость О вполне определяется ее одной проекцией О₃. Углы а и β измеряют углы наклона плоскости О к плоскостям проекций П₁ и П₂ соответственно. n € О, m € О.

4. Плоскость, параллельную какой – нибудь плоскости проекций, называют плоскостью уровня, так как все точки этой плоскостью одинаково удалены от соответствующей плоскости проекций (рис. 2.20).

Плоскость Г, параллельную горизонтальной плоскости проекций, называют горизонтальной плоскостью уровня, а, b € Г.

Плоскость Ф, параллельную фронтальной плоскости проекций, называют фронтальной плоскостью уровня, А, l €Ф.

Плоскость Р, параллельную профильной плоскости проекций называют профильной плоскостью уровня.

Очевидно, что каждая плоскость уровня является в то же время проецирующей плоскостью. Фигуры, принадлежащие горизонтальной плоскости Г, фронтальной плоскости Ф или профильной плоскости Р проецируется без искажения соответственно на плоскость проекций П₁, П₂ или П₃.

2. Взаимное положение точки, прямой и плоскости

Задачи на взаимное положение геометрических элементов называютсяпозиционными.

Точка принадлежит плоскости, если она принадлежит какой – либо прямой этой плоскости. Например, точка К €G (А, В, С), т.к. К € В1 и G1 € О (А, В, С) (рис. 2.21). Очевидно, что N не принадлежит плоскости О, т.к. точка N не принадлежит ни одной из двух прямых АВ или АС. Про точку N можно сказать, что она расположена над плоскостью О, т.к. она расположена над прямой АС. Известно, что точка M € О, а точка L расположена над точкой М, следовательно, точка L находится над плоскостью О.

Задача. Дана восходящая плоскость Э (а ║b), построить точку S над плоскостью, если известна ее горизонтальная проекция S₁ (рис. 2.22).

Точка S₂ должна располагаться над вспомогательной прямой 12, принадлежащей плоскости О и следовательно, над точкой N € 12. Очевидно, что задача имеет бесконечное множество решений.

Обратная задача. Определить положение точки М относительно плоскости R (А, В, С). М ближе R, т.к. М ближе А1 € R (рис. 2.23).

Задача. Построить проекции треугольной пирамиды, основание которой принадлежит данной плоскости Q, а вершина расположена над плоскостью. Определить видимость ребер пирамиды.

Эта задача состоит из трех элементарных задач.

1. Построить вершины А, В, С в плоскости Q. Точки А и В выберем на прямой m, а точку С на вспомогательной прямой В1 (рис. 2.24).

2. Построить точку S над плоскостью Q. Выберем некоторую точку N, принадлежащую Q. На рис. 2.25 эта точка принадлежит В2 € Q. Точка S д.б. над точкой N.

Q (m ║ n) – нисходящая плоскость.

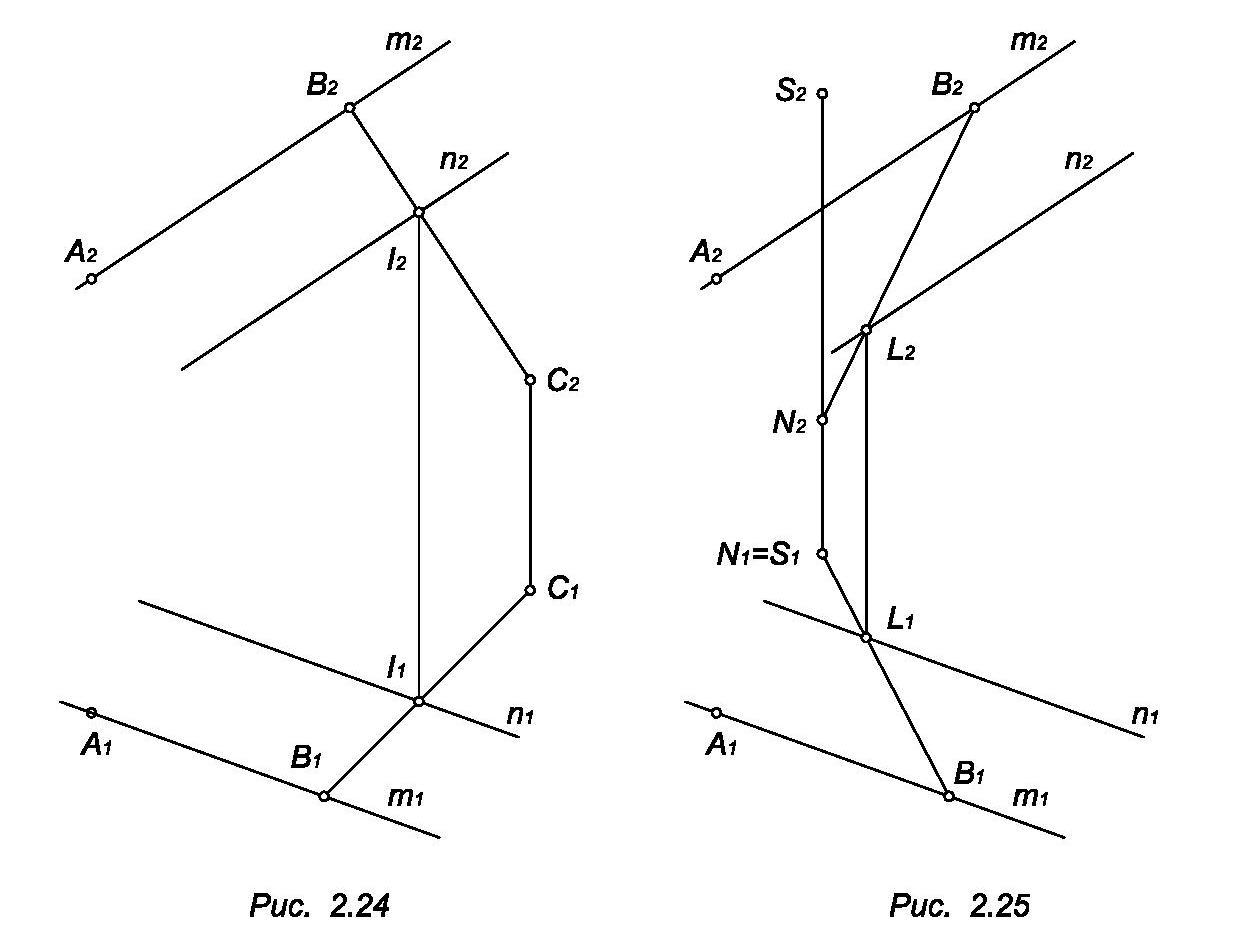
3. На рис. 2.26 повторены эти действия и через полученные точки проведены ребра искомой пирамиды.

Контурные ребра на всех плоскостях проекций всегда видимые.

Для определения видимости ребер АС и SB на горизонтальной плоскости проекций следует воспользоваться горизонтально конкурирующими точками 5 и 6 на этих ребрах. По фронтальной проекции видно, что точка 5 выше точки 6, следовательно, на горизонтальной проекции видимыми являются точка 5 и ребро АС, которому она принадлежит. Аналогично определяется на фронтальной проекции видимость ребер АВ и SC посредством фронтально конкурирующих точек 3 и 4.

2. Кривые линии и их проекции

Понятие о линиях как и о других геометрических объектах приобретается из опыта. Кривую линию можно рассматривать как границу части поверхности, или как результат пересечения двух поверхностей, или как множество последовательных положений непреровно перемещающейся в пространстве точки.

Положение точки на линии может быть определено одним параметром, следовательно, линия является однопараметрическим множеством точек..

Назовем два способа классификации кривых линий:

1. Кривые бывают плоские, пространственные и многомерные.

2. Кривые могут быть закономерными и незакономерными.

Закономерные кривые могут быть заданы и аналитически и графически. Незакономерные задаются только графически.

Взависимости от вида уравнения кривой закономерные кривые бывают алгебраические и транссидентные. Степень алгебраического уравнения определяет порядок кривой. Геометрически порядок плоской кривой определяется по числу точек пересечения ее с прямой, принадлежащей плоской кривой. Точки пересечения могут быть действительными и мнимыми. Например, эллипс пересекается с прямойm в двух действительных точках А и В, с прямой n в двух совпавших действительных точках, с прямой l в двух мнимых точках (рис. 2.27). Если составить уравнение эллипса и прямой m, то, решая их совместно, получим уравнение второго порядка, дискриминант которого положительное число. Во втором случае дискриминант равен нулю, а в третьем - дискриминант отрицателен.

Проекции плоскости кривых линий обладает следующими основными свойствами:

1. В общем случае порядок плоской алгебраической кривой при параллельном проецировании не изменяется.

2. Бесконечно удаленные точки кривой проецируются в бесконечно удаленные точки ее проекций.

3. Касательная к кривой проецируется в касательную к ее проекции

Касательнойt в точке М плоской кривой l будем называть предельное положение секущей ММ^’, когда М, оставаясь на линии l, стремиться к точке М (рис. 2.28). Нормалью n к кривой l в точке М называют прямую, принадлежащую плоской кривой и перпендикулярную к касательной в этой точке.

7. Линии второго порядка

В общем случае кривая второго порядка задается уравнением второго порядка вида:

Аx² +By² + C_xy + D_x + E_y + 1 = 0

(Если свободный член уравнения не равен 1, то обе части уравнения можно разделить на свободный член).

Следовательно, кривую второго порядка определяют пять параметров А, В, С, D, Е. Эти параметры можно вычислить, взяв координаты пяти точек данной кривой. Пусть известны точки: М₁ (x₁y₁), М₂ (x₂y₂), М₃ (x₃y₃), М₄ (x₄y₄) и М₅ (x₅y₅). Для определения коэффициентов А, В, С, D, Е следует решить систему из пяти линейных уравнений:

Аx₁² + Вy₁² + Cx₁y₁ + Dx₁ + Ey₁ + 1 = 0

Аx₂² + Вy₂² + Cx₂y₂ + Dx₂ + Ey₂ + 1 = 0

Аx₃² + Вy₃² + Cx₃y₃ + Dx₃ + Ey₃ + 1 = 0

Аx₄² + Вy₄² + Cx₄y₄ + Dx₄ + Ey₄ + 1 = 0

Аx₅² + Вy₅² + Cx₅y₅ + Dx₅ + Ey₅ + 1 = 0

Следовательно, кривую второго порядка в общем случае можно задавать пятью точками или набором из пяти других геометрических элементов, например, двумя касательными и тремя точками. Подробнее с этим вопросом можно познакомиться по учебнику.

Если кривая второго порядка задана уравнением в общем виде, то пользуясь поворотом и переносом осей координат, ее уравнение можно привести к пяти частным случаям, которые перечислены в таблице 2.1.

Таблица 2.1 Уравнения. Определения и основные понятия кривых второго порядка

Кривая	Основные понятия	Чертеж
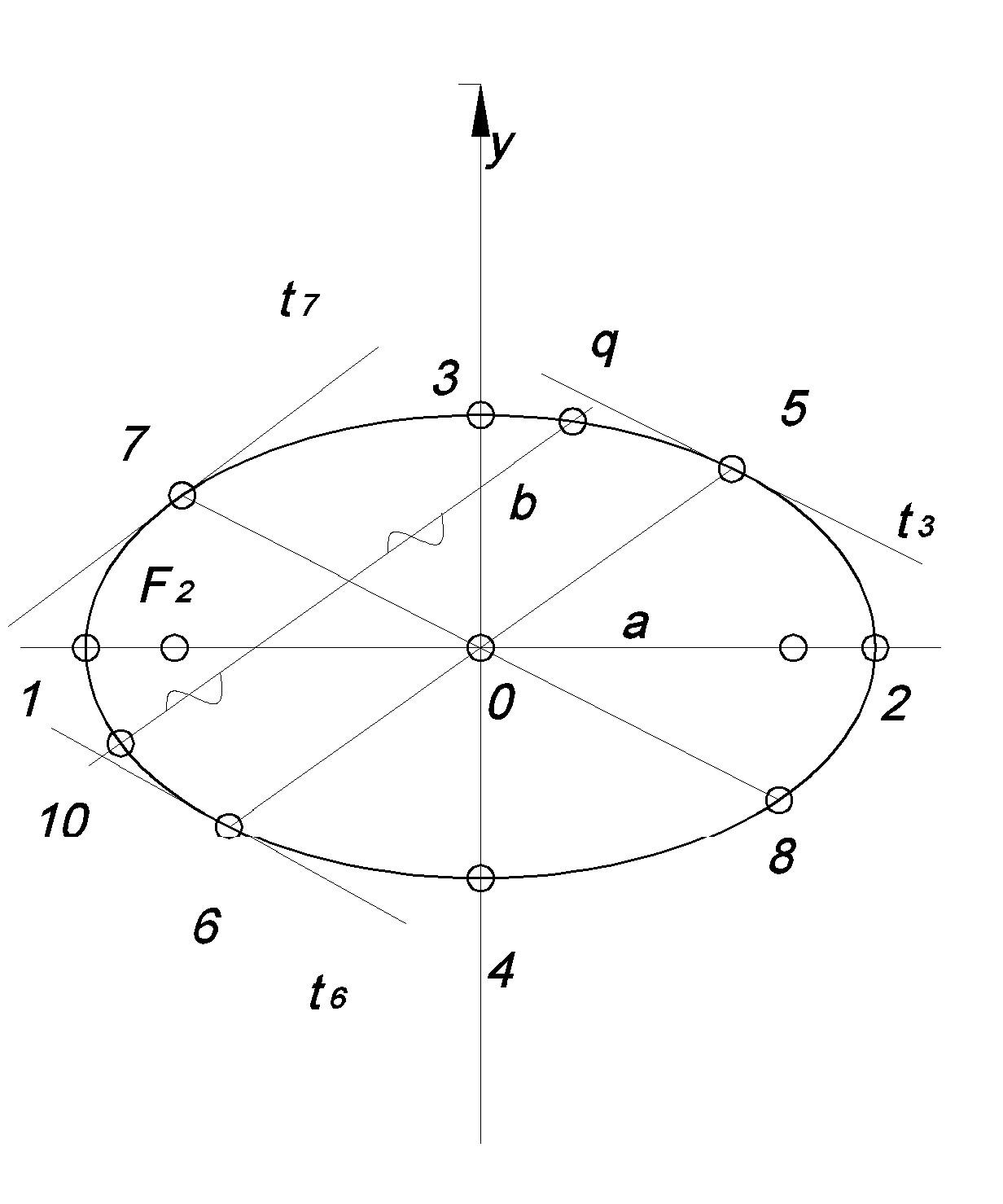
Окружность x^2+ y^2 =R Множество точек равноудаленных от данной точки на данное расстояние Уравнение (x-a)^2 + (y-b)^2 = R^2, где a, b – координаты центра, R – радиус. Если центр в начале координат, то x^2 + y^2 = R^2	/ОМ/ - радиус окружности 12 – диаметр окружности О – центр окружности (12) и (34) – перпендикулярные диаметры окружности t – касательная окружности (56) и (78) – ортогонально – сопряженные диаметры окружности (q10) – хорда ортогонально – сопряженная диаметру (78)
Эллипс + = 1 Множество точек, сумма расстояний которых до двух данных точек F1 и F2, есть величина постоянная.	(12) – большая ось эллипса (34) – малая ось эллипса С,b – большая и малая полуоси эллипса О – центр эллипса F1, F2 – фокусы эллипса /О F1/ = /О F2/ = (56) и (78) – сопряженные диаметры эллипса t5, t6 – касательные эллипса, сопряженные диаметру (56) t5, t7 – сопряженные касательные (910) – хорд, сопряженная диаметру (78)
Парабола X^2 = 2ру Множество точек, для которых расстояние до данной точки F и данной прямой d равны	О – вершина параболы OF – ось параболы t5, - касательная параболы (56) и t5, - сопряженные направления параболы F, d – фокус и директриса параболы. /EF/ = P
Гипербола - = 1 Множество точек, разность расстояний которых до двух данных точек F1 и F2, есть величина постоянная.	1,2 – действительные вершины гиперболы 3,4 – мнимые вершины гиперболы (12) – действительная ось гиперболы (34) – мнимая ось гиперболы (02) – действительная полуось гиперболы (03) – мнимая полуось гиперболы OK и OL – асимптоты гиперболы (56) и t – сопряженные направления гиперболы F1 и F2 – фокусы гиперболы /OF1/ = /OF2/ = /ON/ =

Рассмотрим некоторые способы построения кривых второго порядка.

Задача. Построить эллипс по двум осям (рис. 2.29).

Даны:

АВ – большая ось эллипса

CD – малая ось эллипса

О – центр эллипса

1. Проводим две окружности с центром О и радиусом /ОА/ и /ОС/.

2. L – любая прямая проходящая через О.

Прямая l пересекает окружность в точках K и L.

3. Через точку K (K принадлежит большей окружности) проводим прямую f, параллельную малой оси. Через точку L (L принадлежит малой окружности) проводим прямую h, параллельную большой оси эллипса f ║h = М. М принадлежит эллипсу.

4. Меняя положение прямой l, получим множество точек эллипса, которые следует соединить плавной кривой линией.

Задача. Построить параболу (рис. 2.30)

Даны:

А – вершина параболы

AD- направление оси

В – одна из точек.

1. Строим прямоугольник ACBD/

2. Отрезки АС и СВ делим на произвольное и одинаковое число равных частей и нумеруем точки деления как показано на рисунке.

3. Вершину А соединяем с точками деления отрезка СВ, а из точек деления отрезка АС проводим прямые, параллельные оси.

4. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяет ряд точек параболы.

Вторую ветвь параболы можно построить, пользуясь симметрией относительно AD.

Задача. Построить гиперболу (рис. 2.31).

Даны:

a и b – асимптоты,

а П b = О,

А – некоторая точка гиперболы.

1. Через точку А проведем прямые n и l, параллельные асимптотам b и a соответственно.

2. Через центр гиперболы О проведем произвольную прямую m. m П n = N; m П l =L.

3. Через точку N проведем прямую k, k ║ а; и через точку L прямую r, r ║ b.

4. k П r = B, B – принадлежит искомой гиперболе.

Меняя положение прямой l, получим ряд точек гиперболы.

7. Пространственные кривые

Пространственные кривые задаются системой из двух уравнений y = f(x), z = u(x) или T (x, y, z) = 0, u (x, y, z) = 0, т.е. фактически уравнениями заданы две поверхности, пересечением которых определена кривая.

Для задания пространственной кривой на чертеже необходимы две проекции. На рис. 2.32 изображена пространственная кривая. Очевидно, что эта кривая имеет оду особую (двойную) точку 1. Точки 2 и 3 – различные точки.

3. Поверхности

1. Образование, задание и изображение поверхностей

Поверхность в начертательной геометрии рассматривается как непрерывная совокупность последовательных положений переменной образующей, перемещающейся в пространстве по определенному закону. Таким способом образования поверхности называется кинематическим. Линия при своем движении может оставаться неизменной или непрерывно меняться.

Поверхности могут быть заданы аналитически, то есть уравнением (алгебраические поверхности и трансцендентные) и графически - на чертеже.

На любой поверхности можно выделить два семейства кривых линий: семейство l и семейство m, каждое из которых покрывает всю поверхность и состоит из каких – либо линий (рис. 3.1). При этом должно соблюдаться условие: никакие две линии одного семейства не должны иметь общих точек и наоборот, каждая линия одного семейства должна пересекать все линии другого семейства.

В этом случае поверхность может быть образована движением линии l, называемой образующей, по неподвижным линиям второго семейства m, которые называются направляющими. Нетрудно видеть, что можно поменять местами образующие и направляющие и при этом получается одна и та же поверхность.

Каждая поверхность может быть образована различными способами. Например, поверхность кругового цилиндра может быть образована вращением прямолинейной образующей вокруг оси, ей параллельной; или движением окружности, центр которой перемещается по оси цилиндра, а плоскость окружности перпендикулярна к оси; или вращением произвольной криволинейной образующей, нанесенной на поверхность цилиндра.

Чтобы задать поверхность на комплексном чертеже, необходимо и достаточно иметь совокупность элементов поверхности и условий, которые позволяют построить каждую ее точку или линию. Такую совокупность называют определителем поверхности. Определитель поверхности содержит геометрическую часть и закон образования поверхности или смысловую часть.

Когда какая – нибудь поверхность проецируется параллельно на плоскость проекций, то проецирующие прямые, касаются поверхности в точках, образующих некоторую линию, называемую контурной линией.

Проекция контурной линии называется очерком поверхности.

Для придания чертежу наглядности в большинстве случаев строят на нем еще и очерк поверхности, а так же ее наиболее важные линии и точки.

Принцип образования поверхностей движением линии лежит в основе их изучения в начертательной геометрии. С учетом этого принципа можно сгруппировать поверхности в следующие классы:

1. Поверхности плоско – параллельного перемещения, которые образуются непрерывным параллельным перемещением в пространстве некоторой линии.

2. Поверхности вращения, которые образуются вращением произвольной образующей вокруг неподвижной оси, к их числу относятся поверхности вращения второго порядка.

3. Поверхности второго порядка общего вида

4. Линейчатые поверхности, которые могут быть образованы движением прямой линии, в частности винтовые поверхности, образуемые движением прямолинейной образующей по направляющим винтовым линиям.

5. Циклические поверхности, которые могут быть образованы движением окружности (постоянного или переменного радиуса).

6. Топографические и графически задаваемые поверхности, которые не могут быть образованы по какому – нибудь простому закону и задаются на чертеже семейством некоторых линий (обычно линиями уровня). В этом случае говорят, что поверхность задана дискретным каркасом.

2. Поверхности плоско – параллельного перемещения

Поверхностью плоско – параллельного перемещения называется поверхность образованная параллельным перемещением кривой линией (образующей) по определенному закону. Закон перемещения может быть задан некоторой кривой, называемой направляющей.

Если направляющая m задана уравнением z = f(x), y = 0, а образующая : z = u(y). X = 0 (рис. 3.2), то уравнение поверхности имеет вид:

Z = f(x) + u(y).

Если образующая поверхности – прямая, то поверхность относится также к классу линейчатых поверхностей (цилиндрическая поверхность).

3. Поверхности вращения

Поверхностью вращения называется поверхность, образованная вращением линии (образующей) вокруг некоторой неподвижной прямой (оси вращения). Определитель: Ф (I, l) – поверхность вращения. Геометрическая часть определителя Ф (I, l) должна состоять из оси вращения i и образующей l (рис. 3.3). Смысловая часть содержит информацию о названии поверхности и, следовательно, задает закон образования поверхности.

Каждая точка образующей l при вращении вокруг оси i описывает окружность p (параллель поверхности), расположенную в плоскости, перпендикулярно оси вращения. Центр О окружности p находится в точке пересечения оси вращения с плоскостью окружности, а радиус равен расстоянию от взятой точки образующей до оси вращения.

Наибольшая е и наименьшая g параллели называются соответственно экватором и горловиной (рис. 3.4).

Кривые линии поверхности вращения, плоскость которых проходит через ось вращения, называется меридианами, например , l, m, m^’.

Все меридианы одной поверхности вращения конгруэнтны (рис. 3.5).

На комплексном чертеже целесообразно ось вращения выбирать перпендикулярно одной из плоскостей проекций.

Вкачестве примера рассмотрим комплексный чертеж гиперболоида вращения. Однополостный гиперболоид вращения образуется вращением прямойl вокруг скрещивающейся с ней оси i. Заданием этих элементов на комплексном чертеже поверхность определена, но для решения ряда задач и для наглядного изображения поверхности необходимо строить каркас и очерк поверхности, заданной определителем. На прямой l выберем несколько точек (1,2,3,4,5) и построим проекции параллелей, описываемых этими точками (рис. 3.6).

Например, параллель k проходит через точку 2. Горизонтальная проекция ее – окружность, радиус которой i2. Фронтальная проекция – отрезок прямой конгруэнтный диаметру окружности k. Точки 2 и 2^’ принадлежат фронтальному очерку поверхности f. Меридиан f называется главным меридианом поверхности. Заметим, что главным меридианом рассматриваемой поверхности является гипербола, и, следовательно, гиперболоид вращения может быть образован вращением гиперболы вокруг оси.

На поверхности однополостного гиперболоида имеются два семейства прямолинейных образующих. Образующие каждого семейства между собой скрещиваются, но всякая образующая одного семейства пересекает все образующие другого. Поэтому через каждую точку поверхности можно провести две прямолинейные образующие равных семейств. Т.о., каркас однополостного гиперболоида вращения может быть составлен из множества окружностей или на множестве прямых. Если линии каркаса принять за оси металлических стержней и колец, то получится реальная инженерная конструкция – экономичная, прочная и жесткая. Эта конструкция может служить опорой, мачтой, каркасом гиперболических оболочек.

4. Уравнение поверхности вращения

Пусть известно уравнение главного меридиана поверхности вращения (рис. 3.7):

Z = f(x), y = 0. (3.1)

Тогда точка этого меридиана М (x, O, y) после поворота на некоторый угол t займет положение (,, ) на меридиане . По чертежу видно, что

Z =

X =

= tg t.

Подставляя эти значения в уравнения (3.1), получим систему уравнений, которые задают любой меридиан поверхности вращения:

z = f( )

y = x tg t

Здесь ,, - текущие координаты, следовательно, целесообразно эти уравнения записать в виде:

z = f () (3.2)

y = x tg t (3.3)

Уравнение (3.2) – уравнение поверхности, а уравнение (3.3) – задает плоскость меридиана.

Итак, для того чтобы получить уравнение поверхности вращения, необходимо в уравнение ее главного меридиана вместо переменной x подставить (имеется ввиду, что ось вращения поверхности совпадает с осью Oz).

Используя этот прием, выведем уравнения рассмотренных ранее поверхностей вращения и проведем их краткое исследование.

1. Поверхности, образованные вращением прямой вокруг некоторой оси. К ним относятся поверхности однополостного гиперболоида вращения, конуса и цилиндра вращения.

Математическая модель:

- гиперболоида (см. рис. 3.6) имеет вид:

+ - = 1,

Уравнение главного меридиана: - = 1,

- конуса вращения (см. рис. 3.8) имеет вид:

(z – a)² = k² (x² + y²),

k = tga;

- цилиндра вращения (рис. 3.9) имеет вид:

x² + y² = r²

2. Поверхности вращения, образованные вращением окружности или ее дуги. К ним относятся сфера и тор.

Сфера образуется, если окружность вращается вокруг оси, проходящей через ее центр (рис 3.10). Уравнение сферы имеет вид:

(x – x₀)² + (y – y₀)² + (z – z₀)² = r²,

Где x₀, y_0, z₀ – координаты центра сферы.

На рис. 3.10

а – экватор,

b – главный меридиан,

m – линия, принадлежащая поверхности.

Линия m является плоской кривой, принадлежащей сфере, следовательно, m – окружность. Ее горизонтальная проекция эллипс m₁, большая ось которого А₁В₁, а малая С₁D₁. Это обусловлено тем, что диаметр АВ окружности m параллелен плоскости П₁ и проецируется на П₁ в натуральную величину. Концы диаметра А₁ и В₁ строятся по принадлежности параллели k (k₂ проходит через середину отрезка m₂).

Тор образуется, если окружность вращается вокруг оси, которая не проходит через ее центр, но принадлежит плоскости окружности. Если окружность не пересекает ось вращения, то тор называется кольцом. Тор является поверхностью четвертого порядка. Уравнение тора с центром в начале координат имеет вид:

( – а)² + z² = r².

3. Поверхности вращения второго порядка образуются вращением кривых второго порядка вокруг их осей (рис. 3.11, 3.12). К ним относятся также поверхности, образованные вращением прямой линии.

5. Линейчатые поверхности

Линейчатую поверхность можно рассматривать как непрерывное множество последовательных положений движущейся по определенному закону прямой линии (образующей). Однополостный гиперболоид, цилиндр и конус вращения тоже относятся к линейчатым поверхностям.

В общем случае закон движения образующей может быть задан тремя криволинейными направляющими, которые пересекает любая образующая линейчатой поверхности.

Пусть линейчатая поверхность задана тремя направляющими p, g, f. Выберем на направляющей p произвольную точку А (рис. 3.13). Тогда точка А и направляющая g определяет некоторую коническую поверхность Ф, Ф П f =К. Точки К и А определяют прямолинейную образующую поверхности, заданной тремя криволинейными направляющими. Аналогично строятся и др. образующие линейчатой поверхности.

Если в качестве направляющих выбрать три скрещивающиеся прямые, не параллельные одной плоскости, то образующая поверхности при непрерывном движении опишет однополостный гиперболоид.

Прямолинейная направляющая может быть несобственной (бесконечно удаленной) прямой, тогда она задается плоскостью, которая называется плоскостью параллелизма.

Линейчатые поверхности с плоскостью параллелизма может быть образована движением образующей по двум направляющим при условии, что все образующие параллельны неподвижной плоскости (плоскости параллелизма).

В зависимости от формы направляющих поверхности с плоскостью параллелизма называются: цилиндроидом, когда обе направляющие – кривые (рис. 3.14); коноидом, когда одна направляющая кривая, а другая прямая (рис. 3.15); гиперболическим параболоидом (косой плоскостью), когда направляющие – скрещивающиеся прямые (рис. 3.16). Геометрическая часть определителя таких поверхностей содержит направляющие и плоскость параллелизма.

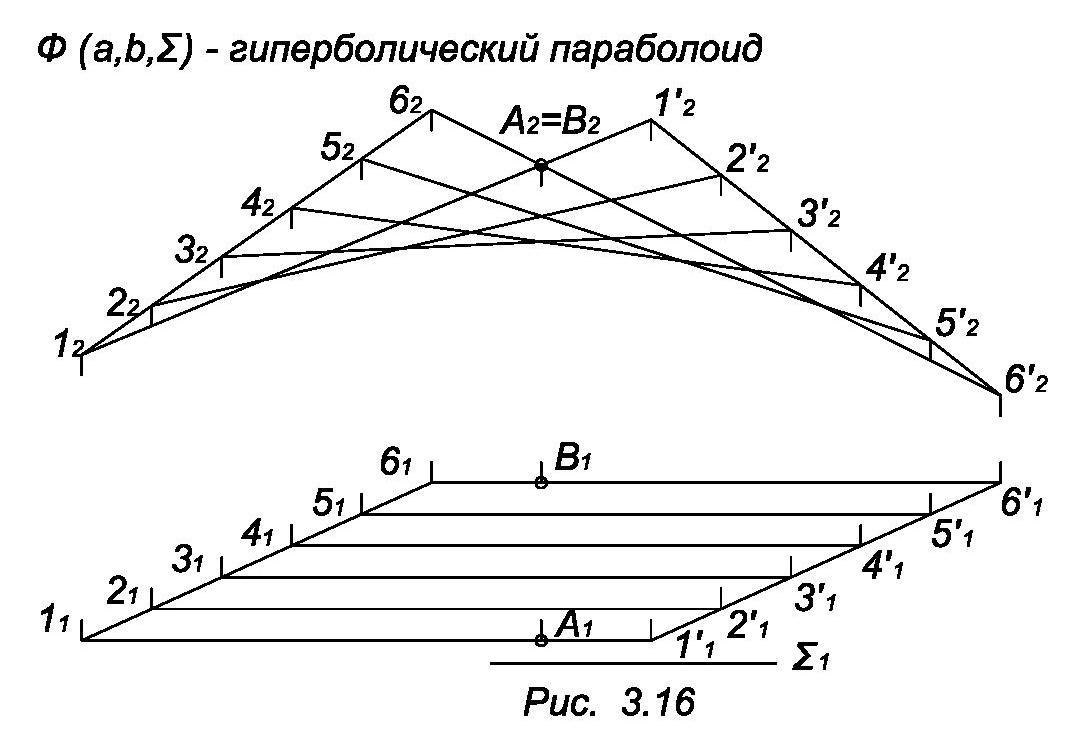
На рис. 3.16 изображен отсек (часть) поверхности. Для определения видимости очерковых образующих 11^’ и 65^’ выбраны конкурирующие точки А и В. Очерковая линия n строится как огибающая фронтальных проекций прямолинейных образующих. Гиперболический параболоид (косая плоскость) относится также к классу поверхностей второго порядка.

Взаимным пересечением образующих косая плоскость разбивается на отдельные, почти «плоские» части, по контуру которых могут быть легко изготовлены и собраны различные оболочки.

Развертывающиеся линейчатые поверхности имеют в своем определителе одну криволинейную направляющую.

Торс образуется движением прямолинейной образующей l, касающейся во всех своих положениях некоторой пространственной кривой (направляющей), называемой ребром возврата.

Торс вполне определяется заданием направляющей. Торс состоит из двух частей, разграниченных по ребру возврата. Ф (а) – торс. Линииm и n принадлежат Ф (рис. 3.17).

Коническую и цилиндрическую поверхности можно рассматривать как частные случаи поверхности торса, когда ее ребро возврата вырождается в точку.

Коническая поверхность образуется движением прямолинейной образующей l, которая пересекает некоторую кривую линию а (направляющую) и проходит через неподвижную точку S (вершину). Ф (а, S) – коническая поверхность (рис. 3.18). Точка М € Ф.

Цилиндрическая поверхность образуется движением прямолинейной образующейl, которая пересекает некоторую кривую линию а (направляющую) и параллельна данной прямой s (рис. 3.19). Ф (а, S) – цилиндрическая поверхность. Линия b € Ф. Видимость на горизонтальной проекции определена с помощью конкурирующих точек К и 5.

Цилиндрическую поверхность можно рассматривать как частный случай конической поверхности, у которой вершиной является бесконечно удаленная точка данной прямой s.

5. Уравнение линейчатой поверхности

Пусть направляющие линейчатой поверхности p, f, g заданы системой уравнений:

z₁ = f₁ (x₁) z₂ = f₂ (x₂) z₃ = f₃ (x₃)

y₁ = u₁ (x₁) y₂ = u₂ (x₂) y₃ = u₃ (x₃)

Уравнение прямой, проходящей через две точки:

= =

Образующая поверхности должна проходить через точки, принадлежащие данным направляющим, следовательно, в уравнении прямой необходимо подставить значения z₁, y₁, z₂, y₂, полученные из уравнения направляющих p и f.

- -;

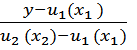И значения z₁, y₁, z₃, y₃ из уравнений направляющих p и g.

- -.

Исключая из полученных четырех уравнений x₁, x₂ и x₃ получим уравнение искомой поверхности.

Пример 1. Составить уравнение косой плоскости, направляющие которой

z₁ = px₁ + g z₂ = ky₂

y₁ = 0 x₂ = 0

и плоскость параллелизма z = 0 (рис. 3.20).

Из условия параллельности прямой (образующей) плоскости Оxy следует, что

z₁ = z₂ = z, и очевидно, что

x₁ = , y₂ = ,

Подставляя эти значения в уравнения прямой, получим

= = или z² – pxz – kyz + kgy – gz = 0

Исследовать это уравнение предлагается самостоятельно.

5. Поверхности второго порядка

Поверхность второго порядка можно определить либо как поверхность, пересекающуюся с произвольной плоскостью по кривой второго порядка (действительной, мнимой или распавшейся на две прямые), либо как поверхность, пересекаемую произвольной прямой, не принадлежащей ей, в двух точках (действительных различных, действительных совпавших, мнимых).

Мы уже познакомились с некоторыми поверхностями второго порядка, которые называют еще квадриками.

1. Конические и цилиндрические поверхности являются поверхностями второго порядка, если их направляющие являются кривыми второго порядка.

Такие поверхности называют еще линейчатыми квадриками.

Если направляющей конической поверхности является эллипс, то поверхность называется эллиптическим конусом (рис. 3.21). Уравнение эллиптического конуса, вершина которого находится в начале координат, имеет вид:

+ - = 0, при а = b это уравнение конуса вращения.

Эллиптический конус и конус вращения занимают особое место среди поверхностей второго порядка, они примечательны тем, что их поверхности содержат все виды кривых второго порядка. К числу второго порядка относятся две прямые (различные или совпавшие). В проективной геометрии принято считать, что прямая содержит одну бесконечно удаленную точку и две параллельные прямые пересекаются в бесконечно удаленной точке. Эллипс и окружность не имеют бесконечно удаленных точек, парабола имеет одну такую точку, а гипербола – две.

На рис. 3.22 задана фронтальная проекция конуса вращения Ф. Плоскость Г пересекает его по окружности, плоскость ∑ - по эллипсу; Л параллельна одной образующей, следовательно, линия пересечения Л и Ф имеет одну бесконечно удаленную точку, т.е. является параболой; P параллельна двум образующим, значит, линия пересечения P и Ф имеет две бесконечно удаленные точки, т.е. является гиперболой; О проходит через вершину конуса, т.е. пересекает конус по двум прямым.

Вместо термина кривая второго порядка применяется также термин коническое сечение или коника.

2. Трехосный эллипсоид:

+ + = 1

Ф (е, g) – эллипсоид.

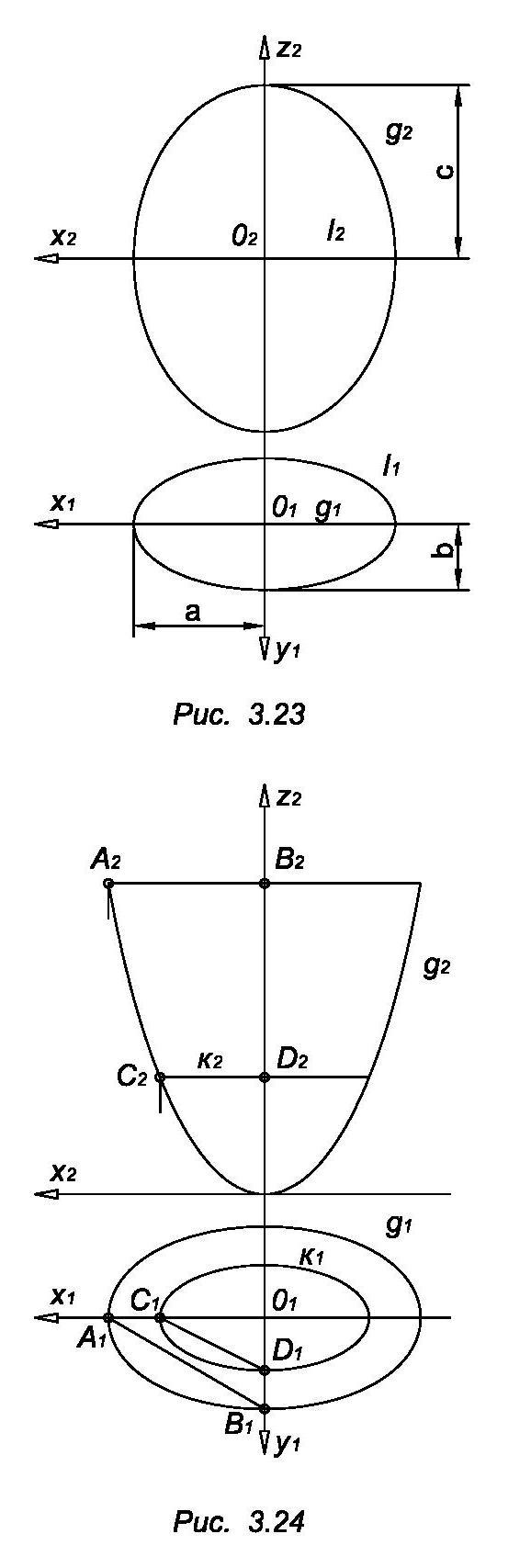
Трехосный эллипсоид может быть задан проекциями очерковых линий. Его горизонталями являются эллипсы, которые подобны горизонтальному очерку (рис. 3.23).

Эллипсоид вращения и сфера являются частными случаями трехосного эллипсоида (см. рис. 3.10 и 3.11).

3. Эллиптический параболоид:

Z = +

Ф (е, g) – эллиптический параболоид (рис. 3.24).

Горизонталями этой поверхности являются эллипсы, подобные эллипсу е. Их горизонтальные проекции подобны и подобно расположены, т.е. гомотетичны. Центром гомотетии является точка О₁. Исходя из этого строится горизонтальная проекция параллели К. если известна К₂. Очевидно, /О₁С₁/ - большая полуось искомого эллипса. Чтобы построить его малую полуось необходимо провести С₁D₁ ║ А₁В₁, как показано на рис. 3.24.

Параболоид вращения является частным случаем эллиптического параболоида.

Гиперболический параболоид рассмотрен в разделе линейчатые поверхности.

4. Однополостный и двуполостный гиперболоиды:

+ - = 1

Ф (е, g) – однополостный эллиптический гиперболоид (рис. 3.25). М € Ф.

Частный случай однополостный гиперболоид вращения

- - + = 1

Ф (е, g) – двуполостный эллиптический гиперболоид (рис. 3.26).

Частный случай - двуполостный гиперболоид вращения.

Следует отметить, что все поверхности второго порядка, за исключением параболического и гиперболического цилиндров, а также гиперболического параболоида, могут пересекаться плоскостью по окружности, т.е. имеют круговые сечения.

5. Циклические поверхности

Циклическими поверхностями называются поверхности, которые образованы движением окружности переменного радиуса по определенному закону. Следовательно, всякой цилиндрической поверхности принадлежит семейство окружностей. Второе семейство линий (направляющих) может состоять из различных кривых в зависимости от закона движения образующих, который задается аналитически или графически.

Одним из видов циклических поверхностей являются каналовые поверхности, которые образуются движением окружности переменного радиуса так, что центр окружности перемещается по заданной кривой (линии центров) l, а плоскость окружности остается перпендикулярной к этой кривой (рис. 3.27).

На комплексном чертеже каналовую поверхность можно задать посредством линии центров и одной из образующих. Линия центров определяет закон движения окружности, а образующая – закон изменения радиуса.

Ф (l, b) – каналовая поверхность. к – одна из образующих Ф.

Горизонтальные проекции образующих можно построить по двум осям. Горизонтальная проекция отрезка строится как огибающая проекция образующих.

5. Пример составления уравнения циклической поверхности

Вкачестве примера рассмотрим циклическую поверхность которая: образуется движением окружности постоянного радиуса. Плоскости окружностей поверхности параллельны между собой, центр окружности М перемещается по прямойf (рис. 3.28). Уравнение линии центров: y₀ = 0, z₀ = x₀.

Уравнение окружности:

(x-x₀)² + (y-y₀)² = z², z = z₀

Где x_0, y_0, z₀ – координаты центра окружности.

Очевидно, что координата точки окружности равна координате z₀ ее центра, следовательно, x₀ = z₀ = z.

Подставляя значения координат центра окружности в уравнение окружности, получим уравнение поверхности:

(x-z)² + y² = r².

Эта поверхность называется эллиптическим цилиндром.

5. Графические поверхности

В инженерной практике нередко возникает необходимость графического отображения процессов или объектов, которые описываются сложными уравнениями, либо для них не существует точной математической модели из-за сложности процесса или недостаточной его изученности. В таких случаях рассматриваемые процессы о объекты моделируются посредством поверхностей, которые на чертеже изображаются при помощи совокупности линий (дискретного каркаса). Такие поверхности называются графическими.

К графическим поверхностям относятся поверхности земной коры, корпуса судна, обшивки самолета, автомобиля, рабочая поверхность лопатки газотурбинного двигателя, поверхность термодинамического потенциала и др. (рис. 3.29). Геометрические модели графических поверхностей несут необходимую информацию и позволяют проводить приближенные расчеты.

4. Взаимное положение поверхностей

Известны три случая взаимного положения поверхностей:

• Поверхности не пересекаются или не имеют общих действительных точек;

• Поверхности касаются, т.е. имеют общие двойные точки или линии;

• Поверхности пересекаются, т.е. имеют одну или несколько общих линий.

Если рассматриваемые поверхности не пересекаются, интерес представляет только задача по определению видимости их контуров, которая может быть решена уже рассмотренными методами.

Случай касания поверхностей рассмотрим на примере касания сферы и плоскости.

Задача: через точку М, принадлежащую сфере, провести плоскость, касательную к сфере (рис. 4.1).

1. Через точку М проведем горизонталь поверхности – окружность k.

2. h – касательная к окружности k в точке М.

3. Через точку М проведем фронталь поверхности n, где n – окружность.

4. f – касательная к окружности n. Пересекающиеся прямые h и f определяют искомую плоскость.

Если поверхности пересекаются, то линию пересечения поверхностей обычно строят по ее отдельным точкам, которые определяются способом вспомогательных секущих поверхностей. Суть его заключается в следующем:

1. Две данные поверхности пересекают некоторой вспомогательной поверхностью.

2. Строят линии пересечения вспомогательной поверхности с данными поверхностями.

3. Определяют общее точки этих линий.

4. Повторяя указанный прием с различными вспомогательными поверхностями, находят такое количество точек, которое графически вполне определяет линию пересечения.

5. После этого полученные точки соединяют с учетом видимости плавной кривой линией с помощью лекала.

Решая задачи на определение линии пересечения поверхностей, следует помнить, что кроме произвольных общих точек линия пересечения имеет особые или спорные точки. Это точки, принадлежащие очерковым линиям, экстремальные точки, точки перегиба и др. Эти точки следует определять по возможности точнее.

В качестве вспомогательных поверхностей следует выбирать такие поверхности, которые пересекают данные по наиболее простым линиям. Чаще всего это плоскости или сферы.

1. Метод вспомогательных секущих плоскостей

Для построения линии пересечения поверхностей во многих задачах удобно использовать совокупность вспомогательных плоскостей уровня.

Задача: построить линию пересечения кругового конуса Q и эллиптического цилиндра Ф (рис. 4.2).

Алгоритм решения задачи:

1. Г – вспомогательная плоскость, Г ║ П₁ (рис. 4.2).

2. Г П Q = p; Г П Ф =g.

3. p П g = М, М^’.

4. Выбираем другие вспомогательные плоскости и повторяем действия с 1 по 3 для каждой из плоскостей, до тех пор пока не будет построено необходимое количество точек (рис. 4.3).

Замечание: в числе вспомогательных плоскостей следует обязательно выбирать плоскости симметрии заданных поверхностей и плоскости крайних параллелей и меридианов. На рис. 4.3 это плоскости Г^” и ∑.

5. Соединяем полученные точки плавной кривой линией с учетом видимости.

Участок линии является видимым только в том случае, если все его точки принадлежат видимой части данных поверхностей.

Для решения задач на взаимное пересечение поверхностей иногда полезно применять методы преобразования комплексного чертежа.

Задача. Построить линию пересечения конуса Q с плоскостью общего положения О.

На рис. 4.4 плоскость О задана горизонталью h и фронталью f. Решение задачи намного упроститься, если с помощью метода замены плоскостей проекций выбрать дополнительную плоскость проекций П₄ так, чтобы данная плоскость проецировалась на нее в прямую. Это станет возможным в том случае, если П_{4 ┴} О.

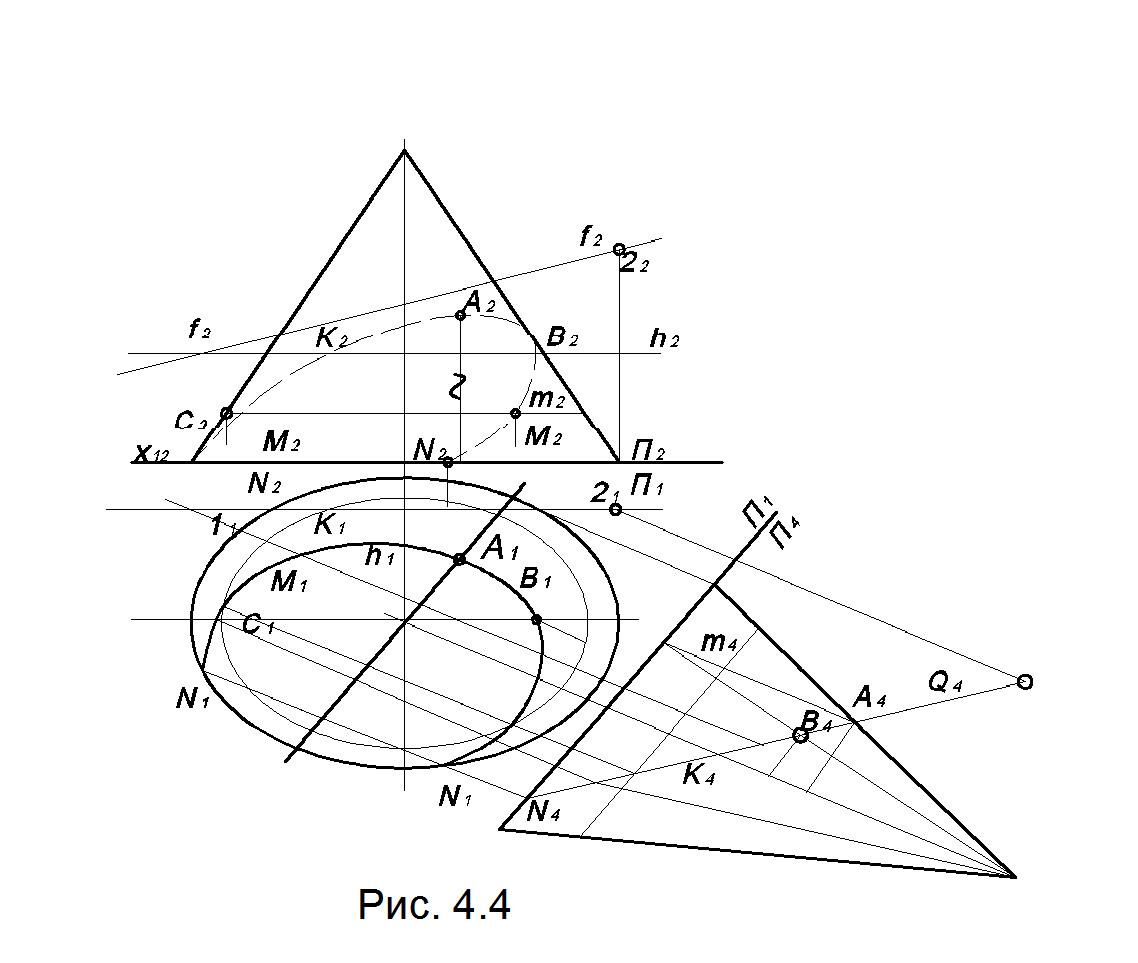
Алгоритм решения:

1. Выбираем П₄, П_{4 ┴} П₁, П_{4 ┴} О, следовательно, x_{14 ┴} . Строим проекции конуса и плоскости О на П₄. Линия пересечения на П₄ спроецируется в отрезок прямой k₄, k₄ = О₄. Чтобы найти О₄ достаточно построить дополнительные проекции двух точек 1 и 2.

2. Выделим на k₄ особые и промежуточные точки, необходимые для построения проекций k₁ и k₂ линии пересечения. К ним относятся точки: А – наивысшая, В и С принадлежат фронтальному очерку, N и N^’ – наинизшие. М и М^’ – промежуточные точки.

3. Построим горизонтальные, а затем фронтальные проекции этих точек по принадлежности конической поверхности или плоскости.

4. Соединим полученные точки плавной кривой линией к с учетом видимости, считая плоскость прозрачной.

При построении линии пересечения конических и цилиндрических поверхностей общего вида целесообразно выбирать вспомогательные секущие плоскости общего положения.

В случае пересечения конических поверхностей эти плоскости должны проходить через вершины конусов, тогда они пересекают обе поверхности по прямолинейным образующим. Если пересекаются цилиндрическая и коническая поверхности, то вспомогательные поверхности должны проходить через прямую, проведенную через вершину конуса параллель образующей цилиндра. В случае же пересечения двух цилиндрических поверхностей вспомогательные плоскости должны быть параллельны некоторой плоскости, определяемой двумя пересекающимися прямыми, соответственно параллельным образующим цилиндрических поверхностей.

2. Метод вспомогательных секущих сфер

Если пересекающиеся поверхности являются поверхностями вращения или содержат семейства окружностей, то в качестве вспомогательных поверхностей целесообразно использовать сферы.

На рис. 4.5 показаны примеры пересечения сферы с конусом вращения и сферы с эллиптическим цилиндром (сферу здесь считаем прозрачной). В первом случае центр сферы принадлежит оси вращения конуса, а во втором – расположен на перпендикуляре, восстановленном из центра окружности поверхности цилиндра к плоскости окружности. Линией пересечения поверхностей в том и другом случае являются окружности.

Рассмотрим на примерах два случая применения вспомогательных сфер.

Методом концентрических сфер можно пользоваться, если выполнены следующие условия:

• Пересекаются две поверхности вращения

• Оси вращения поверхностей пересекаются

• Общая плоскость симметрии поверхностей параллельна плоскости проекций. Это условие не является обязательным.

Задача. Построить линию пересечения конуса вращения Q (а, i) с тором Т (l, j) (рис 4.6).

Пересекающиеся поверхности имеют общую плоскость симметрии Ф, Ф║ П₂, I П j = о. Плоскость Ф пересекает данные поверхности по контурным образующим, которые пересекаются в точках А и В. Эти точки ограничивают фронтальную проекцию линии пересечения, следовательно, радиус наибольшей вспомогательной сферы равен большему из отрезков /О₂В₂/ или /О₂А₂/.

Нетрудно догадаться, что наименьшая сфера должна быть вписана в одну из поверхностей и пересекать вторую поверхность. В данном случае эта сфера вписана в тор. Она касается тора по окружности h и пересекает конус по окружности k. Эти окружности пересекаются, т.к. принадлежат одной сфере, и точки их пересечения С = С^’ принадлежат искомой линии. (Горизонтальная проекция этих точек определяется по принадлежности вспомогательной окружности h).

Чтобы построить промежуточные точки будем выбирать сферы с радиусом больше радиуса минимальной сферы, но меньше радиуса максимальной. Построение промежуточных точек показано на рис. 4.7.

1. R – вспомогательная сфера.

2. R П T = m; R П Q =n.

3. m П n = М.

4. Изменяя радиус вспомогательных сфер, получим необходимое количество точек искомой линии.

5. Полученные точки следует соединить плавной кривой линией с учетом видимости.

Заметим, что точка видимости D на горизонтальной проекции линии пересечения принадлежит горизонтальному очерку цилиндра, поэтому следует предварительно уточнить положение этой точки на фронтальной проекции и затем на горизонтальной.

Метод вспомогательных эксцентрических сфер применяется в тех случаях, когда одна из пересекающихся поверхностей является поверхностью вращения, а вторая содержит семейство окружностей.

Задача. Построить линию пересечения тора Т и сферы Q/

По аналогии с предыдущей задачей строим точки А и В в общей плоскости симметрии Ф. (рис. 4.8).

Точка А в данном случае является наивысшей точкой искомой линии, а точка В – наименьшей. Следовательно, окружность на торе следует выбирать в этих пределах.

Пусть m одна из таких окружностей, m = ∑ П Т. Центры всех сфер, проходящих через эту окружность, принадлежат перпендикуляру n, восстановленному к плоскости окружности из ее центра. Но вспомогательная сфера должна пересекать по окружности и другую поверхность, т.е. центр ее должен быть расположен и на оси вращения i поверхности Q. Следовательно, центром вспомогательной сферы является точка О = I П n, радиусом отрезка О₂К₂, где К₂ – контурная точка окружности m.

Вспомогательная сфера пересекает сферу Q по окружности b. Окружности m и b пересекаются в точках М и М^’, принадлежащих искомой кривой. Меняя положение плоскости ∑ в указанных пределах и повторяя рассмотренные действия, построим необходимое количество точек искомой линии и соединим их плавной кривой линией с учетом видимости (см. рис. 4.8).

2. Особые случаи пересечения поверхностей второго порядка

В общем случае две поверхности второго порядка (квадрики) пересекаются по кривой четвертого порядка, но в некоторых случаях кривая четвертого порядка распадается на:

• Кривую третьего порядка и прямую, если пересекаются линейчатые квадрики (например, цилиндр и конус) с общей образующей;

• Четыре прямые, например, при пересечении двух цилиндров второго порядка с параллельными образующими;

• На две кривые второго порядка (коники).

Случаи, когда линия пересечения квадрик распадается на две коники, а также когда линия пересечения, являясь кривой четвертого порядка, проецируется в кривую второго порядка, перечислены в следующих четырех теоремах.

Теорема 1. Если две квадрики имеют общую плоскость симметрии, параллельную плоскости проекций, то линии их пересечения на эту плоскость проецируются в кривую второго порядка.

На рис. 4.3 пересекаются квадрики с общей плоскостью симметрии ∑, ∑ ║ П₂, следовательно, линия пересечения этих квадрик симметрична относительно ∑, и каждая пара симметричных точек на П₂ спроецируется в одну точку, т.е. порядок проекции линии пересечения уменьшится в два раза, и кривая пересечения четвертого порядка спроецируется на П₂ в кривую второго порядка.

Теорема 2. Если две квадрики имеют общую конику, то линия их пересечения распадается на две коники. Доказательство этой теоремы тривиально: 4-2-2. Пример применения теорем 1 и 2 показан на рис. 4.9.

Эллиптические конус и цилиндр имеют общую окружность m – это одна часть линии пересечения данных поверхностей. Другая часть линии пересечения – коника k, на плоскость П₂ она проецируется в отрезок прямой k₂, т.к. поверхности имеют общую плоскость симметрии Ф. Следовательно, для построения k₂ достаточно найти две точки, проще всего построить точки А и В с помощью вспомогательной плоскости ф. Если точка В₂ недоступна, то можно построить любую точку искомой линии, например М, воспользовавшись вспомогательной плоскостью Г.

Следующие две теоремы приведены без доказательства.

Теорема 3 (теорема Монжа). Если две квадрики описаны около третьей (или вписаны в нее), то линии их пересечения распадается на две коники.

На рис. 4.10 конус и цилиндр описаны около сферы, следовательно, линией их пересечения являются две коникиm и n, причем, их фронтальные проекции m₂ и n₂ – отрезки прямых, т.к. общая плоскость симметрии Ф данных поверхностей параллельна П₂. Общими точками данных поверхностей являются точки А, В, С, которые построены с помощью вспомогательной плоскости Ф.

Особыми точками искомой линии пересечения являются точки К и К^’. Эти точки строятся как точки пересечения окружностей касания a и b сферы к конусу и цилиндру. Особенность точек К и К^’ обусловлена тем, что это точки прикосновения данных поверхностей и принадлежат каждой из линий m и n. Горизонтальные проекции линий m и n следует строить по принадлежности к одной из данных поверхностей.

Замечание. Точкой прикосновения двух поверхностей называется точка, через которую можно провести общую касательную плоскость к этим поверхностям.

Теорема 4. Линия пересечения двух квадрик, имеющих двойное прикосновение, распадается на две коники, которые проходят через точки прикосновения.

На рис. 4.11 показан пример, иллюстрирующий эту теорему.

Сфера и эллиптический конус имеют две точки соприкосновения А и А^э, следовательно, линия их пересечения распадается на две коники m и n, их профильные проекции – отрезки m₃ и n₃, т.к. общая плоскость симметрии Р параллельна П₃. m € А, n € А. Горизонтальная и фронтальная проекции этих линий строятся по принадлежности сфере или конусу.

В данном случае линии m и n – окружности, т.к. они являются плоскими кривыми, принадлежащими сфере. Плоскости, параллельные плоскости одной из этих окружностей, пересекают данный эллиптический конус по окружностям. Т.о., поверхность эллиптического конуса содержит два семейства окружностей. Аналогично можно построить круговые сечения на любой квадрике, кроме косой плоскости и гиперболического и параболического цилиндроидов и конусов.

5. Метод вращения

В разделе 1.6 рассмотрен метод замены плоскостей проекций.

Н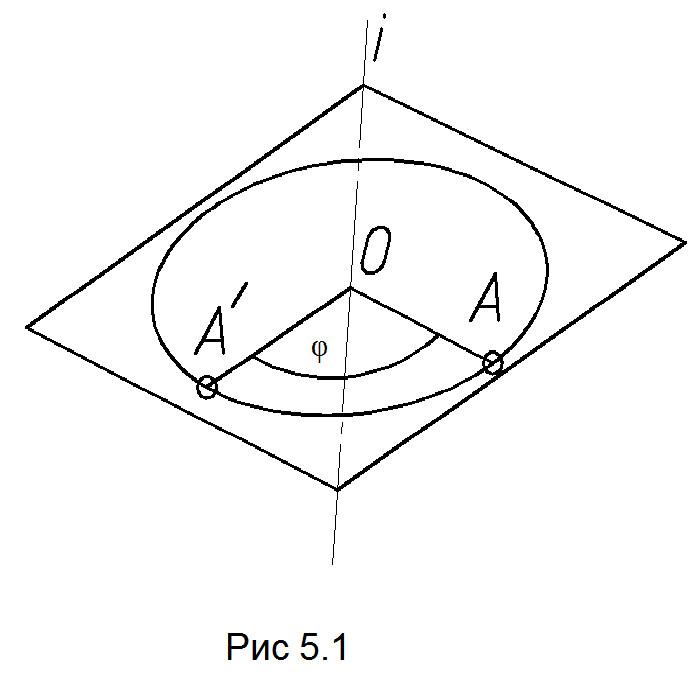е менее важным является и метод вращения. Большинство задач, в которых применяется метод замены плоскостей проекций, могут решены и методом вращения. На выбор того или иного метода влияют требования компактности чертежа, простоты построения, наглядности и др. факторы.

При применении метода вращения положение плоскостей проекций не изменяется, а перемещается геометрический объект. Перемещение геометрического объекта достигается посредством вращения его вокруг некоторой оси. В качестве оси вращения обычно выбирают проецирующую прямую или прямую, параллельную одной из плоскостей проекций.

Следует помнить, что в процессе вращения вокруг оси вращающаяся точка описывает окружность, расположенную в плоскости, перпендикулярной оси вращения i. Центр окружности принадлежит оси вращения. Все точки геометрического объекта поворачиваются на один и тот же угол u. Точки, принадлежащие оси вращения, остаются неподвижными (рис. 5.1).

Вращение вокруг проецирующей прямой рассмотрим на примере вращения точки.

Задача. Повернуть точку вокруг горизонтально проецирующей прямой i на угол u, u = 60⁰ (рис 5.2).

Плоскость, в которой перемещается точка при вращении, перпендикулярна оси вращения i, следовательно, параллельна плоскости П₁. Значит, на плоскость П₁ дуга окружности, которая является траекторией движения точки, спроецируется в натуральную величину. Это же можно сказать и про угол поворота.

Центр дуги принадлежит оси вращения, следовательно, горизонтальная проекция центра дуги – точкаi₁.

Плоскость вращения точки перпендикулярна фронтальной плоскости проекций, следовательно, фронтальная проекция этой дуги – отрезок прямой, перпендикулярной i₂.

Итак, k₁ и k₂ – проекции траектории вращения точки А. На k₁ от точки А₁ следует отложить отрезок дуги, равный 60⁰. А^’ – искомая точка, фронтальная проекция ее определяется по принадлежности k.

Аналогично можно рассмотреть вращение вокруг фронтально проецирующей прямой.

Метод вращения для более сложных задач можно применять неоднократно, а также в сочетании с методом замены плоскостей проекций. Например, если ось вращения прямая общего положения, то следует, посредством метода замены плоскостей проекций, преобразовать ее в прямую частного положения и затем выполнить вращение.

6. Пересечение линии и поверхности

Для определения точек пересечения линии и поверхности необходимо выполнить следующие действия:

• Через данную линию провести вспомогательную поверхность

• Построить линию пересечения вспомогательной поверхности с данной

• Точки пересечения полученной кривой с данной являются искомыми точками пересечения линии и поверхности.

Если данная кривая является прямой линией, то в качестве вспомогательной поверхности целесообразно выбирать проецирующую плоскость или, в некоторых случаях, плоскость общего положения. Иногда полезно при решении задач пользоваться методами преобразования поверхностей.

Задача. Найти точки пересечения прямойl со сферой, определить видимость прямой (рис. 6.1).

1. Через прямую l проведем фронтально проецирующую плоскость ∑.

2. Плоскость пересекает сферу по окружности К, горизонтальная проекция которого эллипс k₁. (Эллипс k₁ можно построить по большой А₁А₁^’ и малой В₁С₁ осям или по отдельным точкам, которые строятся на линиях каркаса).

3. Точки M и N пересечения кривой k с прямой l являются искомыми.

4. Для определения видимости прямой следует оценить сначала видимость точек M и N. По горизонтальной проекции видно, что точка М расположена на ближней половине сферы, следовательно, на фронтальной проекции она видимая, точка N на фронтальной проекции невидимая, т.к. расположена на дальней половине сферы. Аналогично по фронтальной проекции определяется видимость точек М и N на горизонтальной проекции. Отрезок MN находится внутри сферы, поэтому невидимый на любой проекции. Видимость прямой вне этого отрезка совпадает с видимостью рассмотренных точек. Например, на горизонтальной проекции отрезок прямой правее точки М закрывается сферой.

В этой задаче l является прямой общего положения, поэтому плоскость ∑ не параллельна плоскости П₁, и проекция окружности k₁ – эллипс. Построение эллипса проводится приближенно, следовательно, приближенным является и решение задачи на рис. 6.1.

Задачу можно решить точнее, если выбрать дополнительную плоскость проекции П₄ параллельно плоскости ∑ (рис. 6.2), тогда окружность k на П₄ спроецируется в окружность k₄, l₄ строится по точкам 1 и 2. K₄ П l₄ = М_4, N_4.

Если прямая l пересекает ось вращения данной поверхности, то для решения задачи целесообразно воспользоваться методом вращения (рис. 6.3).

1. Повернем прямую l вокруг оси i так, чтобы она стала фронтальной прямой l^’. (Для этого достаточно повернуть некоторую точку А, а точку В остается неподвижной, т.к. принадлежит оси вращения). На тот же угол и вокруг той же оси поворачивается сфера. Очевидно, что ее изображение на чертеже не изменятся. Найти точки пересечения прямой l^’ со сферой просто, т.к. вспомогательная плоскость ∑^’ (∑^’ € l^’ и ∑^’ ┴ П₁) пересекает сферу по главному меридиану m.

m П l^’ = M^’ : N^’.

Вращая сферу и прямую l в противоположном направлении, следует вернуть их в первоначальное положение. Тогда точка M^’ и N^’ на прямой l займут положения М и N.

При построении точек пересечения прямой с цилиндрическими или коническими поверхностями вспомогательную поверхность можно выбрать так, чтобы она пересекала данную поверхность по прямым. Такая плоскость в общем случае является плоскостью общего положения, но пользоваться ею целесообразно, т.к. удается избежать построения кривых линий. Следует заметить, что направляющей поверхности в этом случае должна быть плоская кривая.

Задача. Найти точки пересечения прямой l с конической поверхностью Ф. Определить видимость прямой.

На рис. 6.4 показано решение этой задачи с помощью вспомогательной плоскости частного положения.

1. ∑ € l; ∑ ┴ П.

2. ∑ П Ф = к. (Для построения к здесь воспользовались каркасом данной поверхности, который состоит из прямолинейных образующих).

3. к П l = М,N

4. Определить видимость l.

На рис. 6.5 задача решена посредством вспомогательной плоскости, проходящей через вершину конуса и прямую l.

1. Q (l,S) – вспомогательная плоскость.

2. Построим линии пересечения Q с конусом Ф. Для этого следует выполнить следующие действия:

• А – любая точка прямой l. Через вершину конуса S и точку А проведем прямую m, т.е. плоскость Q теперь задана пересекающимися прямыми l и m.

• ∑ - плоскость, проходящая через направляющую к данной поверхности.

∑ П Q = (12)

(12) П а = В,С.

SB и SC – прямые пересечения плоскости Q с конусом.

3. SB П l = M;

SC П l = N/

M и N – искомые точки.

В случае задания цилиндрической поверхности прямую m следует проводить параллельно образующим этой поверхности.

7. Математическая модель линии пересечения поверхностей второго порядка

Геометрические и аналитические модели и алгоритмы, рассмотренные в этом курсе, могут быть использованы при согласовании программ для решения многих геометрических и специальных задач на ЭВМ.

Например, задача на построение линии пересечения поверхностей второго порядка.

Общее уравнение квадрики имеет вид:

a₁₁x² + a₂₂y² + a₃₃z² + a₁₂xy + a₁₃xz + a₂₃yz + a₁x + a₂y + a₃z + a₀ = 0

Если коэффициенты этого уравнения не равны нулю, то уравнение квадрики, плоскость симметрии которой являются плоскости общего положения. На практике чаще встречаются задача, в которых плоскости симметрии поверхностей параллельны плоскостям проекций. В обобщенном уравнении таких поверхностей некоторые коэффициенты равны нулю или связаны определенным отношением. Например, трехосный эллипсоид, однополостный гиперболоид, эллиптический параболоид, конус и цилиндр могут быть описаны таким уравнением:

+ + К + P (z – z₀) = D

Коэффициенты этого уравнения имеют определенный геометрический смысл. Вид квадрики зависит от значений коэффициентов Р, К и D, размеры от значений А, В, и С и положение относительно координатных плоскостей от х₀, у₀, z₀.

Возможны следующие частные случаи.

1. При Р = 0, К = 1, D = 1, уравнение имеет вид:

- - = 1

Это уравнение трехосного эллипсоида, у которого х₀, у₀, z₀ – координаты центра; А, В, С – соответствуют значениям длин полуосей.

Если А=В=С, то это уравнение сферы, радиус которой равен А.

2. При D =1, К = -1, Р = 0, уравнение имеет вид:

+ - = 1

Это уравнение эллиптического однополостного гиперболоида, у которого х₀, у₀, z₀ – координаты центра гиперболы; А и В соответствуют значениям длин полуосей горловины рассматриваемой поверхности; С – значение мнимой полуоси гиперболы (главного меридиана) (рис. 3.7.3)

3. При D = 0, К = -1, Р = 0, уравнение имеет вид:

- - = 0

Это уравнение эллиптического конуса, у которого х₀, у₀, z₀ – координаты вершины конуса; А и В полуоси направляющего эллипса (основания конуса); С – высота конуса. Если А=В, то это уравнение конуса вращения.

4. При D = 1, К = 0, Р = 0, уравнение имеет вид:

+ = 1

Это уравнение эллиптического цилиндра, поверхность которого является горизонтально проецирующей; х₀, у₀, z₀ – координаты центра направляющего эллипса, причем z может быть любое; А и В – значение полуосей направляющего эллипса.

5. При D = 0, К = 0, Р = -1, уравнение имеет вид:

+ = + (z – z₀₎

Это уравнение эллиптического параболоида, у которого х₀, у₀, z₀ – координаты вершины; А и В – значение полуосей горизонтали расположенной на расстоянии h = 1 от вершины параболоида. Если h = h₀, то значение А и В можно определить по формулам:

А = ; В = ;

Где А₀ и В₀ соответствуют значениям полуосей параллели на высоте h₀.

Если р = -1, то ветви параболы (меридианов поверхности) направлены вверх, если р = 1, то вниз.

Расшифровка значений необходимых коэффициентов показана в таблице 7.1

Таблица 7.1

	Сфера	Трехосный эллипсоид	Однополостный параболоид	Эллиптический конус	Эллиптический цилиндр	Эллиптический параболоид
x	x0	x0	x0	x0	x0	x0
y	y0	y0	y0	y0	y0	y0
z	z0	z0	z0	z0	z0 – любое	z0
А	R сферы	А полуось по оси х	А полуось по оси х	А полуось по оси х	А полуось по оси х	А =
В	R сферы	В – полуось на оси у	В – полуось на оси у	В – полуось на оси у	В – полуось на оси у	В =
С	R сферы	С – полуось на оси z	С – мнимая ось	0 - высота	Любое действительное не равное 0	Любое действительное не равное 0
D	1	1	1	0	1	0
K	1	1	-1	-1	0	0
P	0	0	0	0	0	≠ 1

Математической моделью линии пересечения поверхностей является система уравнений, описывающих данные поверхности. Чтобы получить уравнение горизонтальной проекции линии пересечения, следует решая эти уравнения совместно, исключить z, а для фронтальной проекции – у.

При разработке алгоритма для машинного решения задачи этот путь зачастую не является рациональным из-за сложности уравнений проекций линии пересечения. Поэтому следует воспользоваться геометрическим алгоритмом построения линии пересечения поверхностей, изложенного в главе 4.

Например, по заданным значениям параметров D, K, Р, А, В, С, х₀, у₀, z₀ получены уравнения двух квадрик:

+ + К + P (z – z₀) = D;

+ + К + (z – ) = .

Задавая значения z = z_n, получим уравнения двух коник. В рассмотренных случаях это – уравнения эллипсов, оси симметрий которых принадлежат прямой, параллельной оси Оx. Следовательно, их совместное решение сводится к решению уравнения второго порядка, в результате которого определяются координаты точек линий пересечения. Варьируя z_n можно получить достаточное количество точек этой линии.

Замечание. В тех случаях, когда общая плоскость симметрии данных поверхностей не параллельна плоскости проекций, прежде чем определить параметры х₀, у₀, z₀, полезно применить метод замены плоскостей проекций (раздел 1.6), выбирая дополнительную плоскость проекции параллельно общей плоскости симметрии и задачу решать в новой системе плоскостей проекции и связанной с ней системе координат.

Аналогично составляются алгоритмы для построения линии пересечения с помощью ЭВМ двух любых поверхностей, имеющих математические модели. Причем в некоторых случаях не обязательно составлять уравнение данной поверхности, а можно ограничиться заданием уравнений линий, входящих в определитель поверхности.

8. Метрические задачи

Кроме позиционных задач в технической практике приходится решать задачи, в которых выясняется вопрос измерения отрезков и углов, определения натуральной величины или формы плоских фигур и т.д. Такие задачи называются метрическими. При их решении существенную роль играют условия перпендикулярности прямых и плоскостей на комплексном чертеже.