10.1 Коэффициенты искажения

При проецировании координатных осей на аксонометрическую плоскость масштабные отрезки проецируются с некоторым искажением, если координатные оси не параллельны аксонометрической плоскости. Пусть единичный отрезок е на оси Ох проецируется на аксонометрическую плоскость в отрезок : единичный отрезок на оси у – в отрезок , на оси z - . Тогда отношения:

U = , V = , W = называются коэффициентами искажения.

Обычно на практике аксонометрические координатные отрезки измеряют натуральным масштабом е. Поэтому построение аксонометрического чертежа проводится не по аксонометрическим масштабам , , , а по заданным искажениям U, V, W.

2. Основная теорема аксонометрии

Меняя положение прямоугольной декартовой системы координат относительно аксонометрической плоскости и направления проецирования, можно получать множество различных вариантов положения аксонометрических осей (исключая случайные их совпадения) и различные аксонометрические масштабы. Поэтому возникает вопрос о том, возможно ли произвольно выбрать аксонометрические оси и масштабы.

Ответ на этот вопрос дает теорема Польке.

Всегда найдется такое положение прямоугольной декартовой системы координат в пространстве и такой единичный масштабный отрезок, а также такое направление проецирования, что любая аксонометрическая система окажется параллельной проекцией данной системы координат.

Следовательно, различных аксонометрических проекций существует бесконечное множество, но на практике обычно пользуются только некоторыми из них.

2. Основные виды аксонометрических проекций

Выбор аксонометрических проекций детали обусловлен различными требованиями, основными из которых являются наглядность и простота построения.

ГОСТ 2.317 – 69 устанавливает следующие виды аксонометрических проекций. (рис. 10.1)

Самыми наглядными из перечисленных аксонометрий являются прямоугольная изометрия и прямоугольная диметрия. В дальнейшем подробнее рассматривается простая в построении и самая наглядная прямоугольная изометрия. Косоугольные фронтальная и горизонтальная изометрии менее наглядные, но очень просты при изображении деталей, которые содержат большое количество окружностей, расположенных в параллельных между собой плоскостях.

В прямоугольной изометрии оси образуют углы 120⁰, ось z – вертикальная. Аксонометрические проекции ломанных линий, кривых и дуг окружностей больших радиусов строят по координатам отдельных точек. Для этого на комплексном чертеже данного геометрического объекта задают проекции осей координат и измеряют координаты нужных точек. На рис. 10.2 показано построение аксонометрической точки А по координатам этой точки х, у, z.

На рис. 10.3 дан комплексный чертеж плоской кривой k и построена аксонометрическая проекция по координатам точек.

Построение изометрии многогранника рассмотрим на примере шестиугольной призмы (рис.10.4). На комплексном чертеже правильной шестиугольной призмы следует задать проекции осей координат и построить аксонометрические проекции точек А, К, В, С, учитывая, что /О₁А₁/ = /О^’A^’/, /О₁К₁/ = /О^’К^’/, /К₁В₁/ = /К^’В^’/, /А₂С₂/ = /А^’С^’/.

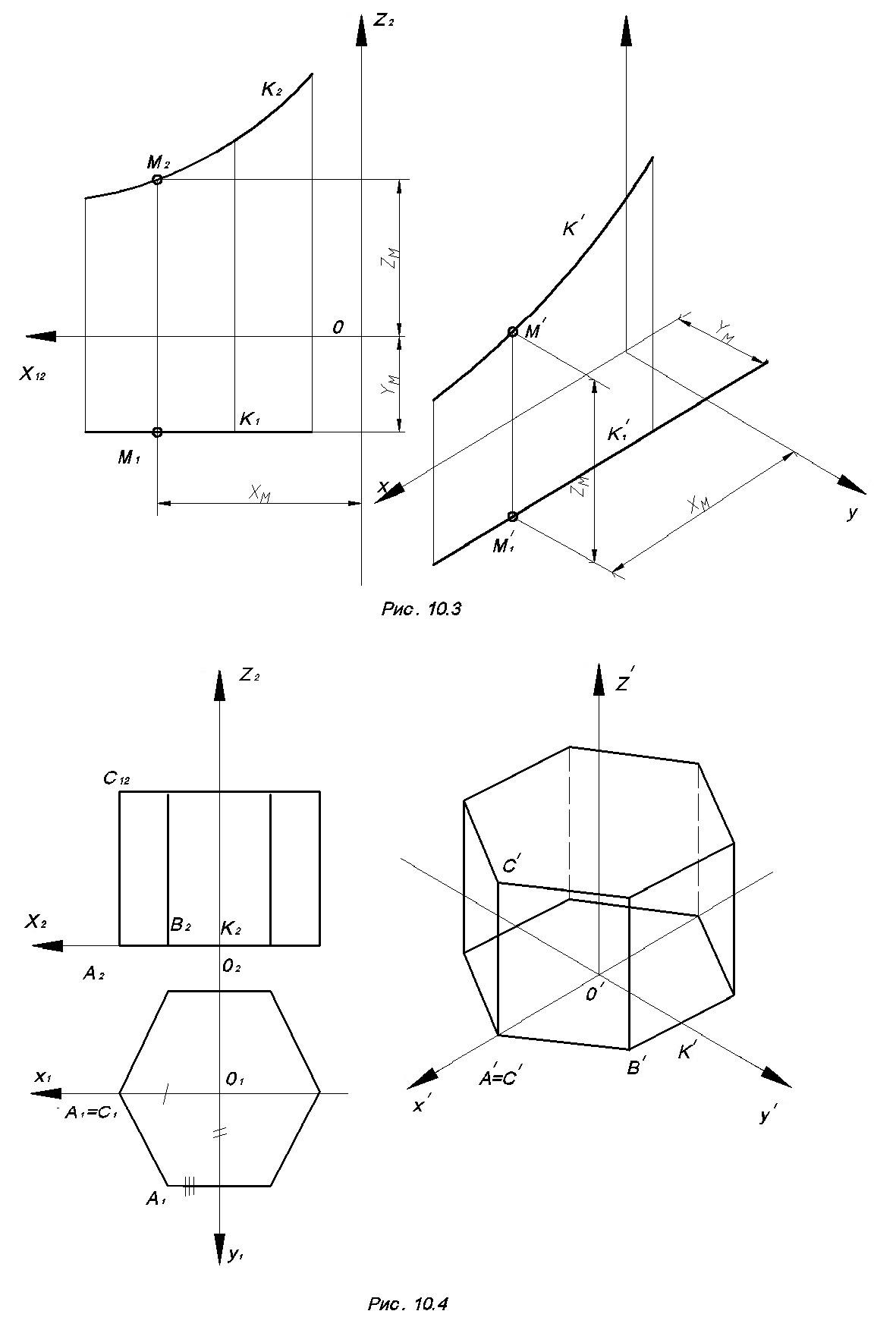
Остальные вершины призмы строятся аналогично.

Окружность плоскость которой параллельна одной из координатных плоскостей в прямоугольной изометрии изображается эллипсом. Форма эллипсов одинакова независимо от того какой из координатных плоскостей параллельна окружность. В инженерной графике принято такие эллипсы заменять четырехцентровыми овалами. На рис. 10.5 показано построение овала, который заменяет изображение окружности в плоскости хОу в прямоугольной изометрии.

1. Проводим вспомогательную окружность К, радиус не равен радиусу данной окружности. Точки 1 и 2 – первые два центра дуг овала.

2. Делим окружность на 6 равных частей, как показано на рис. 10.5., и из центров 1 и 2 проводим дуги а и b.

3. Для определения центров 3 и 4 овала на горизонтальном диаметре от точки М вправо и влево следует отложить отрезки равные малой полуоси эллипса /MN/.

4. Точки сопряжения больших и малых дуг расположены на линиях центров 13, 23, 24 и 14.

Направление главных осей эллипса зависит от того, какой из координатных плоскостей параллельна плоскость рассматриваемой окружности. Если плоскость окружности параллельна плоскости, содержащей две аксонометрические оси, то направление осей эллипса определяется по направлению третьей аксонометрической оси. Большая ось эллипса перпендикулярна этой оси, а малая ей параллельна (рис. 10.6).

Если плоскости окружностей не параллельны ни одной из координатных плоскостей, то эллипсы, изображающие эти окружности, отличаются не только направлениями большой и малой оси, но и их отношением. Существует много способов построения таких эллипсов. Один из них – построение по точкам. Этот способ требует кропотливой и очень тонкой работы, поэтому целесообразно рассмотреть следующий способ. На комплексном чертеже следует определить диаметры окружностей К, которые в изометрии спроецируются в большую и малую оси эллипса К^’ (рис. 10.7), затем найти их изометрическую проекцию (рис. 10.8) и построить эллипс по двум полученным осям.

В прямоугольной изометрии плоскости, равнонаклонные к изометрическим осям, параллельны картинной плоскости. Следовательно, все отрезки, принадлежащие этим плоскостям, проецируются на аксонометрическую картину в натуральную величину (с учетом коэффициента искажения). Поэтому на комплексном чертеже данной окружности К (К₁,К₂) выберем некоторую плоскость Л ( * h), которая равнонаклонена к координатным плоскостям, т.е. ее фронталь f составляет углы 45⁰ с плоскостями хОу и zОу, а горизонталь h углы 45⁰ с плоскостями хОz и zОу. Найдем линию 12 пересечения плоскости Л с плоскостью окружности К, и проведем диаметр А₁В₁ эллипса К₁ параллельно 1₁2₁.

Диаметр АВ проецируется в изометрии в большую ось А^’B^’ искомого эллипса. Диаметр С₂D₂ эллипса К₂ строится как сопряженный диаметру А₁В₁., изометрическая проекция его С^’D^’ является малой осью искомого эллипса К^’. Остается на рис. 10.6 построить эллипс по двум осям. В том же порядке решается задача, если плоскость окружности является плоскостью общего положения, хотя несколько усложняются построения на комплексном чертеже. В этом случае полезно воспользоваться методом замены плоскостей проекций.

Построение некоторых сложных кривых можно проводить непосредственно на изометрической проекции. Например, Ф построить линию пересечения цилиндра с плоскостью Л (рис. 10.9).

Линию построим по отдельным точкам и алгоритм построения каждой точки рассмотрим на примере построения точек К и Т.

Пусть плоскость Л задана параллельными прямыми m (m^’, m₁^’) и n (n^’, n₁^’), а цилиндр Ф направляющей а и направлением образующей l. Тогда прямая p является линией пересечения плоскости Л с плоскостью направляющей а. Дальнейшие построения выполняются в следующем порядке:

1. Проводим вспомогательную плоскость ∑, ∑ ║ хОу.

2. ∑ П Ф = k,t; ∑ П Л = d.

3. T П d = Т, k П d = К.

4. Меняя положение плоскости ∑, получим множество точек, которые определят искомую кривую b^’.

Аналогично решается задача на построение линии пересечения двух цилиндров (рис. 10.10).

Пусть цилиндр Ф задан направляющей а и направлением образующих х, а цилиндр Q – направляющей с и направлением образующих z.

Найдем линию пересечения p плоскости А направляющей а с плоскостью Г направляющей с:

1. хОz П А = m, xOz П Г = n/

2. m П n = M/

3. p € M, p ║ y.

Для построения точек искомой линии следует проводить вспомогательные плоскости.

1. ∑, ∑ ║ xOz.

2. ∑ П Г = g, ∑ П А = h (g и h пересекаются в точке на прямой p).

3. g П с = К,F; h П a = T,E.

4. Через точки К и F проходят образующие k и f цилиндра Q, а через точку Т образующая t цилиндра Ф (точка Е и образующая, проходящая через нее, из рассмотрения исключаются т.к. в пересечении участвует только верхняя часть цилиндра Q).

5. k П t = N, f П t = L,N и I точки искомой кривой.

6. Меняя положение плоскости ∑, получим необходимое количество точек для построения искомой кривой l.

В числе вспомогательных плоскостей следует выбирать плоскости, касательные к цилиндру меньшего радиуса.

Задача на построение линии пересечения цилиндра и конуса в аксонометрии решается с помощью вспомогательных секущих плоскостей, проходящих через вершину конуса и параллельных образующим цилиндра (рис. 10.11).

Пусть цилиндр Ф задан направляющей а и направлением образующих z, а конус Q – направляющей с и вершиной S.

Найдем линию пересечения p и плоскости Г направляющей а с плоскостью ∑ направляющей с:

1. zOy П Г = m, zOy П ∑ = n.

2. m П n = М.

3. р € М, р║ x.

Вспомогательные плоскости должны проходить через прямую h, h € S и h ║ z, h П Г = S^*.

1. Л, Л € h.

2. Л П Г = g, Л П ∑ = d (g и d пересекаются в точке на прямой р).

3. g П а = К; t П с = F, E.

4. Через точки E и F проходит образующие e и f конуса Q, а через точку К образующая k цилиндра Ф.

5. k П е = N, k П f = L. N и L точки искомой кривой.

6. Меняя положение плоскости i, получим необходимое количество точек для построения искомой кривой l.

В числе вспомогательных плоскостей следует выбирать плоскости, касательные к конусу.

Построение изометрии детали сложной формы рассмотрим на следующих примерах.

Пример 1. Полусфера пересекается с двумя цилиндрами вращения Ф и Q (рис. 10.12).

Оси цилиндров проходят через центр полусферы, ось цилиндра Ф параллельна плоскости П₂, ось цилиндра Q – прямая общего положения. Следовательно, линией пересечения цилиндра с полусферой является окружность а, плоскость которой является фронтально проецирующей. Аналогично расположена окружность b. Линия пересечения цилиндра Q c полусферой – окружность общего положения с, в плоскости, ей параллельной, расположена окружность d.

Прежде чем переходить к построению изометрии, на комплексном чертеже найдем диаметры окружностей а или b, с или d, которые проецируются в большие оси эллипсов а^’ и b^’, c^’ и d^’. Эти диаметры должны быть параллельны плоскости Л, равнонаклонненной к координатным плоскостям. Плоскость Л зададим фронталью f (f₂ составляет углы 45⁰ с осями О₂х₂ и О₁z₁) и горизонталью h (h₁ составляет углы 45⁰ с осями О₁х₁ и О₁у₁). Плоскость Л пересекает плоскость окружности а, по прямой 12. Диаметр m окружности b, параллельна 12, проецируется в изометрии в большую ось эллипса b^’. Сопряженный с m диаметр n проецируется в изометрии в малую ось эллипса b^’.

Построение пар сопряженных диаметров k и i окружности d проведем с помощью той же плоскости Л. Здесь целесообразно выбрать дополнительную плоскость проекций П₄, перпендикулярную плоскостям окружностей с и d и плоскости П₁.

Изометрию детали начнем строить с полусферы (рис. 10.13). Ее экватор расположен в плоскости хОу и проецируется в эллипс, который можно заменить четырехцентровым овалом. Очерковой линией r^’ сферы в изометрии всегда является окружность.

Полуокружность r^’ должна касаться к экватору. Для эллипсов b^’ и d^’ по точкам строятся большая и малая оси и эллипсы строятся по двум осям. Эллипс а^’ конгруэнтен эллипсу b^’, а с^’ – эллипсу d^’, поэтому для построения этих эллипсов достаточно найти их центр и воспользоваться конгруэнтностью.

Пример 2. Построить изометрию каналовой поверхности Ф, заданной на комплексном чертеже (рис. 10.14). Каркас этой поверхности состоит из четырех окружностей а, b, c, d. Проекции окружностей а и d в изометрии являются эллипсами, которые можно заменить четырехцентровыми овалами (см. рис. 10.6). Для построения изометрии окружностей b и c следует на комплексном чертеже найти диаметры, которые проецируются в большую и малую оси эллипсов. Зафиксируем систему координат и выберем плоскость Л (f*h), равнонаклоненную к координатным плоскостям. Она пересекает плоскость ∑ по прямой 12 и плоскость ∑^’ по прямой 13. Диаметр m окружности b, m ║ 12, проецируется в изометрии в большую ось эллипса b^’ (рис. 10.15). Проекция П₁ на комплексном чертеже строится как сопряженный с m₁ диаметр эллипса b₁, n^’ – малая ось эллипса b^’. Эллипс b^’ строится по двум осям. Аналогично проводятся построения эллипса с^’. Очерковая линия является огибающей изометрических проекций линий каркаса а^’, b^’, c^’, d^’.

В тех случаях, когда деталь содержит большое количество окружностей, плоскости которых параллельны одной из координатных плоскостей, целесообразно пользоваться косоугольной фронтальной или косоугольной горизонтальной изометрией. На рис. 10.16 выполнена косоугольная фронтальная изометрия такой детали. Проекциями двух окружностей в горизонтальных плоскостях являются эллипсы, которые можно заменить четырехцентровыми овалами.

Построения проекции горизонтальной окружности показано на рис. 10.17.

1. Для конкретной детали следует определить положение центра О^’ изометрической проекции данной окружности. Через точку О^’ провести изометрические оси в плоскости окружности. Построить ромб, стороны которого параллельны изометрическим осям, точки М^’, K^’, N^’, L^’ – середины сторон этого ромба, /О^’M^’/ = /О^’N^’/ = /О^’K^’/ = /О^’L^’/ = r, r^’ – радиус данной окружности.

2. Провести диагонали ромба, и на них отметить точки А^’, В^’, С^’, D^’, /О^’A^’/ = /О^’B^’/ = 1,3 r; /О^’С^’/ = /О^’D^’/ = 0,54 r.

3. По большой А^’В^’ и малой С^’D^’ осям можно построить эллипс или заменить его лекальной кривой, проходящей через точки А^’, М^’, D^’, K^’, B^’, N^’, C^’, L^’, или построить овал следующим образом: центры 1 и 2 принадлежат малой оси, /01/ = /02/ = /А^’В^’/, центры 3 и 4 принадлежат большой оси, /А3/ = /В4/ = 0,25 /С^’D^’/. Из центров 1 и 2 следует провести большие дуги овала, а из центров 3 и 4 – малые. Точки сопряжения дуг Е^’ и F^’ принадлежат линиям центров 13, 23, 14, 24.

ЛИТЕРАТУРА

1. Вальков К.И. Лекции по основам геометрического моделирования / ЛИСМ – Л, 1970.

2. Котов И.И., Якунин В.И., Иванов Г.С. Обводы точек на плоскости. Учебное пособие по начертательной геометрии на базе ЭВМ – М., МАИ, 1977.

3. Четверухин Н.Ф., . . . Курс начертательной геометрии. – М, 1956.

4. Посвянский А.Д. Курс начертательной геометрии. – М., Высшая школа, 1974.

5. Четверухин Н.Ф., Проективная геометрия. – М, 1961.

6. Виницкий И.Г. Начертательная геометрия. – М., Высшая школа, 1975.

7. Павлова Л.А., Лютиков К.И. Конспект лекций по начертательной геометрии / РАТИ. – Рыбинск, 1959. – 50с.

90