1.4. Дискретные случайные величины

Случайной называют величину X, которая в результате одного испытания примет одно и только одно возможное значе, напередие неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной случайной величиной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величиныX называют соответствие между возможными значениями(xi) и их вероятностями (pi); его можно задать таблично, аналитически (в виде формулы) и графически.

Функцией распределения дискретной случайной величиныX называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее x

F(x) = P(X<x).

Математическое ожидание дискретной случайной величины:

M(X) = x1p1 + x2p2 +…+ xnpn

или

¥

M ( X ) = åxi pi ,

i=1

если количество возможных значений X бесконечно. Дисперсия дискретной случайной величины

D(X) = M(X – M(X))2 = M(X2) – (M(X))2.

Среднее квадратическое отклонение случайной величины

σ( X ) = D( X ).

Для случайной величины, распределенной по закону Бернулли, математическое ожидание и дисперсия равны соответственно

M(X) = n×p; D(X) = n×p×q.

8

1.5. Непрерывные случайные величины

Непрерывной		случайной	величиной называют			случайную	величину,
которая	может	принимать	все	значения	из	некоторого	конечного и

бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Функцией распределения непрерывной случайной величины называют непрерывную и кусочно-дифференцируемую функциюF(x), определяющую вероятность того, что случайная величинаX в результате испытания примет значение, меньшее x

F(x) = P(X<x).

Другими словами, непрерывной случайной величиной называют случайную

величину с непрерывной функцией распределения.

Свойства функции распределения

1.

0 £ F(x) £ 1;

2.

F(x) – неубывающая функция;

3.

Вероятность того, что случайная величина примет значение, заключенное

в интервале (a; b),

равна приращению

функции распределения

на

этом

интервале P(a < X < b) = F(b) – F(a);

4.

Вероятность того, что непрерывная случайная величина примет одно

определенное значение, равна нулю;

5.

Пределы в бесконечности

lim F (x) = 0, lim F (x) =1.

x®-¥

x®+¥

6.

Если

все

возможные

значения

случайной величины

принадлежат

интервалу (a; b), то F(x) = 0 для x £ a, F(x) = 1 для x ³ b.

Плотностью

распределения

вероятностейнепрерывной

случайной

величины X

называют функцию f(x)

– первую

производную

от

функции

распределения F(x)

F (x + D x) - F (x)

f (x) = F '(x) = lim

.

Dx®0

D x

Вероятность попадания случайной величины в заданный интервал

b

P(a £ X < b) = ò f (x)dx.

a

Нахождение

функции

распределения

вероятностей

по

известно

плотности

9

x

F (x) = ò f (t)dt .

-¥

Свойства плотности распределения вероятностей:

1. Плотность распределения вероятностей– неотрицательная функция;

¥

2.ò f (x)dx =1 (условие нормировки).

-¥

Математическое ожидание непрерывной случайной величины

¥

M ( X ) = òxf (x)dx.

-¥

Дисперсия непрерывной случайной величины

¥	¥
D( X ) = ò(x - M ( X ))2 f (x)dx = òx2 f (x)dx - M ( X )2 .
-¥	-¥

1.6.Основные виды непрерывных распределений

I.Равномерное распределение.

Плотность	распределения				равномерно					распределенной	случайной
величины
			ì0, x < a;
			ï			1
			ï
		f (x) = í						, a	£ x £ b;
			ïb			- a
			ï0,			x > b.
			î
Функция распределения равномерно распределенной случайной величины
			ì0, x < a;
			ï			- a
			ïx
		F (x) = í						, a	£ x £ b;
						- a
			ïb
			ï1, x > b.
			î
Математическое		ожидание			равномерно					распределенной	случайной
величины

10

M(X) = (b + a)/ 2.

Дисперсия равномерно распределенной случайной величины

D(X) = (b – a)2/12.

Вероятность попадания в интервал(α; β) Í [a; b] равномерно распределенной случайной величины

P(α < X < β) = β - α . b - a

II.Нормальное распределение

Плотность	распределения			нормально						распределенной	случайной
величины
	f (x) =		1						-(x-a )2
									e 2σ2 .
			σ 2π
Функция распределения нормально распределенной случайной величины
			1				x -(t -a 2)
	F (x) =						òe 2σ2 dt.
		σ		2π
						-¥

Математическое ожидание нормально распределенной случайной величины

M(X) = a.

Дисперсия нормально распределенной случайной величины

D(X) = s2.

Вероятность попадания в интервал(α; β) нормально распределенной случайной величины

	æb - a ö			æ a - a ö
	P(α < x < β) = F (b) - F (a) = Fç		÷	- Fç		÷,
		s			s
	è		ø	è		ø

где

11

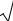
		2π	x
			ò
F(x) =		1		e-t 2 / 2 dt – функция Лапласа (см. таблицу в Приложении).

0

Свойства функции Лапласа:

1)F(–x) = – F(x);

2)F(x) = 0,5 при достаточно больших x.

III.Показательное распределение

Плотность	распределения	показательно	распределенной	случайной
величины

ì0, x < 0;

f (x) = íîλ e-λ x , x ³ 0.

Функция	распределения	показательно	распределенной	случайной
величины

ì0, x < 0;

F (x) = íî1 - e-λx , x ³ 0.

Математическое	ожидание	показательно	распределенной	случайной
величины

M(X) = 1/λ.

Дисперсия показательно распределенной случайной величины

D(X) = 1/λ2.

Вероятность попадания в интервал(α; β) (α, β >0) показательно распределенной случайной величины

P(α < x < β) = e-λα - e-λβ .

12