КУРС сопромата с примерами

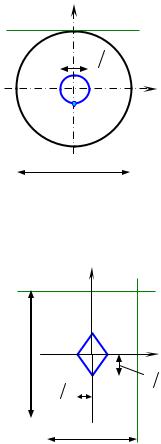
соответствующие им координаты точек ядра сечения (точки 1, 2, 3):

	i2			i2y
yя = yP = −	z	;	zя = zP = −		.	(8.13)
				zн.л.
	yн.л.

Так как при переходе нейтральной линии с одной стороны на другую (например, от н.л 3 к н.л 4) она поворачивается вокруг угловой точки сечения, то точка приложения силы перемещается по прямой (на рис. 8.10 отрезок 3 – 4), образуя контур ядра.

Пример 8.4. Построить ядро сечения для круга диаметром d.

Решение. Квадрат радиуса инерции круга:

iz2 =	Iz		=	πd 4	4	= d 2 .
	A			64	πd 2
						16
Задаем положение нейтральной линии 1–1, касательной к окружно-
сти. Ее координаты:
zн.л 1 = ∞; yн.л 1 = d/2.						1	y	1
Координаты точки ядра сечения:

zя1

= −

i2y

= −

d 2

= 0;

d 4

zн.л.1

16 ∞

z

2

2

1

yя1 = −

iz

= − d

2 = − d .

yн.л.1

16 d

8

d

Из симметрии сечения относительно его центра тя-

жести следует,

что при

других положениях ней-

тральной линии на окружности диаметром d точки ядра сечения образуют

концентрический с ней круг диаметром d/4.

Пример 8.5. Построить ядро сечения для

1

y

2

прямоугольника с размером сторон b×h.

Решение. Квадраты радиусов инерции:

1

iz2 =

I

z

=

bh3 1

=

h2

;

i2y

=

I y

=

b3h 1

=

b2

.

h

2

z

12 bh

12

A

12 bh

12

A

h 6

Задаем положение нейтральной линии 1-1, ка-

b 6

1

сательной к верхней грани прямоугольника. Ее ко-

ординаты: zн.л 1

= ∞;

yн.л1 = h/2. Координаты соот-

b

2

ветствующей точки ядра сечения:

i2y

b2

i2

h

2 2

h

zя1 = −

= −

= 0;

yя1 = −

z

= −

= −

.

zн.л1

12 ∞

yн.л1

12 h

6

Аналогично для нейтральной линии 2-2: zн.л 2 = b/2;

yн.л 2 = ∞.

i2y

b2

2

b

i2

h2

z

я

2

= −

= −

= −

;

y

я2

= −

z

= −

= 0.

yн.л2

zн.л2

12 h

6

12 ∞

100

Учитывая симметрию прямоугольного сечения относительно осей z и y, задаем положения нейтральных линий на противоположных сторонах прямоугольника и получаем еще две точки. Соединяя все точки, получаем

ядро сечения в виде ромба с диагоналями, равными h/3 и b/3.

I

h

III

IV				y			II	Пример 8.6. Построить ядро сечения для
							I	швеллера № 20.
				3				Решение. Из таблицы сортамента выпишем ис-
2					4			ходные данные и выполним рисунок швеллера.
							z	Последовательно задаем положение нейтраль-
								ной линии (I-I, II-II, III-III, IV-IV), касающейся контура
				1				сечения, и вычисляем координаты точек ядра сечения.
								Расчеты представлены в табличном виде.
							III	Ядро сечения имеет вид четырехугольника,
					z0
								асимметричного относительно оси ординат. Положе-
				b
								ние ядра сечения зависит лишь от формы и раз-
IV							II	меров поперечного сечения, но не зависит от вели-
								чины приложенной силы.

yн.л. = h/2 = 20/2 = 10 см;

zн.л. = ∞;

i2y

I-I

1

yя

= −

iz2

= −

8,072

= −6,51 см;

zя

= −

= −

2,2

2

= 0;

yн.л.

10

zн.л.

∞

II-

yн.л. = ∞;

zн.л. = b – z0= 7,6–2,07 = 5,53 см;

yя

= −

iz2

= −

8,072

= 0 ;

i2y

2,2

2

II

2

zя

= −

= −

= 0,845 см;

yн.л.

∞

zн.л.

5,53

III-

yн.л. = –h/2 = –20/2= –10 см;

zн.л. = ∞;

i2y

yя

= −

iz2

= −

8,072

= 6,51 см;

2,2

2

III

3

zя

= −

= −

= 0;

yн.л.

−10

zн.л.

∞

IV-

yн.л. = ∞;

zн.л. = – b = –2,07 см;

yя

= −

iz2

= −

8,072

= 0 ;

i2y

2,22

IV

4

zя

= −

= −

= 2,34 см;

yн.л.

∞

zн.л.

− 2,07

Расчет на прочность при внецентренном нагружении

Поверочный расчет выполняют, используя условие прочности

σ =

N

±

M z

±

M y

≤ [σ].

Wy

A

Wz

Проектный расчет обладает особенностью, связанной с тем, что геометрические характеристики, входящие в условие прочности содержат искомый размер поперечного сечения в разной степени. Площадь А измеряется в м2, а моменты сопротивления W в м3. Попытка выразить искомый

101

размер из условия прочности приводит к трансцендентной функции, то есть аналитической функции, не являющейся алгебраической.

Проектный расчет выполняют методом итераций1 [от лат. iteratio –

повторение]. В первом приближении, пренебрегая одним из внутренних усилий, – продольной силой N – подбирают размер сечения только из условия прочности при изгибе. Полученный размер подставляют в исходное уравнение и выполняют следующую пробу. Процесс повторяют до тех пор, пока невязка – разность размеров последующей и предыдущей проб, не достигнет заданной наперед малости.

Пример 8.7. (Винокуров А. И. Сборник задач … 5.35).

Подобрать диаметр стержня выпускного клапана. При расчете использовать усилие F в момент открывания клапана в конце рабочего хода поршня.

Дано:

p = 1,5 МПа;	e = 12 мм;
D = 35 мм;	[σ] = 210 МПа

F	F				Решение. Сила давления газов на та-
			релку клапана			= p π D2 =1,5	π352 =1443 Н.
e	e			F = p A
					клап	4	4
1	1	М			Внутренние усилия в сечении 1-1 стер-
	N		жня клапана (по модулю):
						N = F; M = F·e.
	d		Условие прочности:
		σmax		= N	+ M ≤ [σ];	σmax = F 4 + F e 32 ≤ [σ].
p	D			A	W	πd 2	πd 3
		4F					4F
				(d +8e)≤ [σ],
		πd 3				откуда d ≥ 3 π[σ](d +8e).

По обе стороны от знака неравенства искомый диаметр – имеем трансцендентное уравнение, которое решаем методом приближений:

d0 = 0; d1 ≥ 3 4π 1443210 (0 +8 12)= 9,435 мм. d2 ≥ 3 4π 1443210 (9,435 +8 12)= 9,735 мм. d3 ≥ 3 4π 1443210 (9,735 +8 12)= 9,744 мм.

1 Метод последовательных приближений, при котором каждое новое приближение вычисляют исходя из предыдущего; начальное приближение выбирается в достаточной степени произвольно.

102

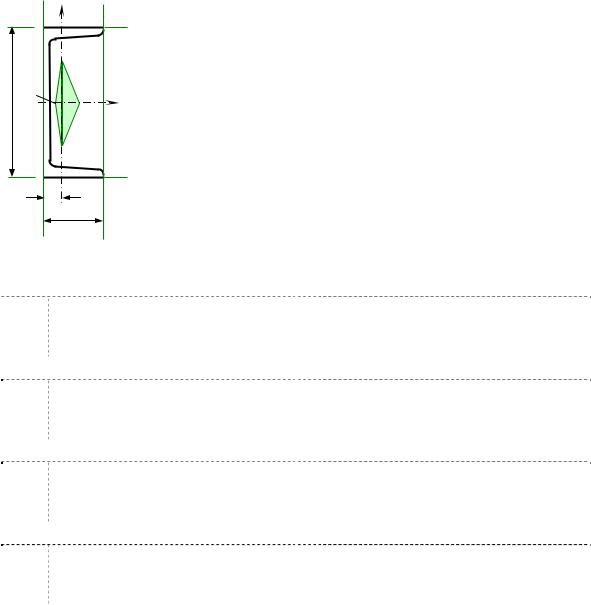
Разность между последним и предпоследним приближениями

9,744 − 9,735

100 = 0,0924 % .

9,744

Процесс подбора прекращаем, принимаем d = 10 мм.

σ = F 4

+ F e 32

Проверка:

=

1443 4 + 1443 12 32

=18,4 +176,4 =194,8 МПа.

πd 2

πd 3

π 100

π 1000

Напряжения изгиба больше напряжений растяжения в

σизг

=

176,4

= 9,6 раза.

σраст

18,4

Пример 8.8. (Винокуров А. И. Сборник задач …

5.38.).

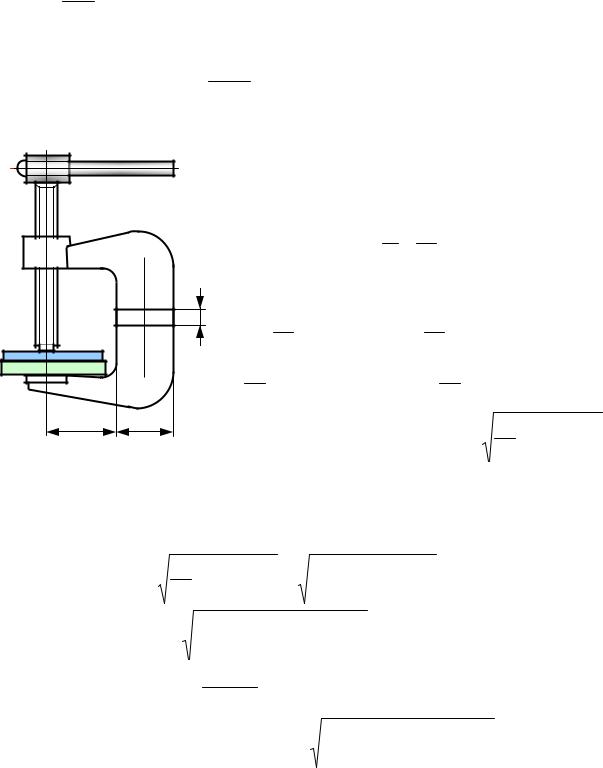
Из расчета на прочность определить размер

h скобы струбцины.

Решение.Условие прочности при вне-

центренном растяжении плоской фигуры

σ =

F

+ M

≤[σ],

A

W

b

где

A = b·h; W = b·h2/6;

M = F(a+h/2).

Условие прочности:

σ =

F

+ F (a +h / 2)6 =

F

+ 6Fa

+ 3Fh

≤[σ];

bh

bh2

bh

bh2

bh2

F h

+6

a

+3

h

≤[σ];

F

h

+6

a

≤[σ].

h2

b

h2

4

b

b

a

b

b

h

Требуемый размер скобы:

h ≥

F

4

h

+ 6

a

b

b

.

[σ]

Размер h в обеих части неравенства. Полученное уравнение

– транс-

цендентное. Решаем его методом последовательных приближений. В пер-

вом приближении принимаем h в скобках под корнем равным нулю: h0 = 0.

Тогда

h =

F

4

0

+

6

a

=

16000

0

+6

90

= 77,46 мм;

b

b

90

16

1

[σ]

h2 =

16000

4

77,46

+6

90

= 97,17 мм.

90

16

16

Невязка подбора

h2 − h1 100 = 97,17 − 77,46100 = 25,4 % .

h1

77,46

Следующее приближение

h3 =

16000

4

97,17

+ 6

90

=101,58 мм.

90

16

16

103

Невязка подбора

h3 − h2

100 = 101,58 − 97,17100 = 4,5 % .

h3

97,17

Следующее приближение

h4 =

16000

4

101,58

+ 6

90

16

16

=102,54 мм.

90

Невязка подбора

h4 − h3

100 = 102,54 −101,58100 = 0,95 % .

h4

101,58

Последняя невязка менее 1 %, поэтому выходим из цикла подбора.

Принимаем h = 103 мм.

F

M

Проверка:

σ =

+

=

16000

+

16000 6

90 +

103

A

W

16 103

16

2

; σ = 9,71 + 80,03 =89,74 МПа <[σ].

1032

Сопоставим вклады от изгиба и растяжения в общее напряжение:

σизгσ = 8980,,7403 = 0,892. σрастσ = 899,,7174 = 0,108.

Напряжения от изгиба в 8,24 раза превышают напряжения от растяжения. Полученное соотношение можно сделать более благоприятным снизив долю растягивающих напряжений от изгиба за счет уменьшения

плеча е изгибающего момента. На практике применяют тавровое и двутавровое сечения, смещая центр тяжести с ближе к линии действия силы и располагая больше материала в области растягивающих напряжений, к которым хрупкие материалы более чувствительны.

Линия действия силы

с

с

е

с

Рис. 8.11. Примеры выполнения поперечного сечения бруса, подверженного действию внецентренного растяжения

104

8.3. ИЗГИБ С КРУЧЕНИЕМ

Изгиб с кручением – вид сложно-

го сопротивления, при котором в поперечном сечении бруса возникают изгибающие и крутящий моменты.

Рассмотрим случай, при котором внешние силы располагаются в плоскости поперечного сечения, но не пересекают геометрическую ось х (рис. 8.12, а). Силу F разложим на ее составляющие Fz, Fy. Методом сечений определим внутренние усилия в произвольном се-

чении х (рис. 8.12, б).

Спроецировав все силы на координатные оси и составив уравнения моментов относительно координатных осей, найдем внутренние усилия. Из шести внутренних усилий не равно нулю пять.

Fz	y х
		а
	е
F	Fy
x		z
		y
	Mz	б

My Qz Qy В

x T z

Рис. 8.12. Определение внутренних усилий при изгибе с кручением

Σ x = 0;	N = 0;	Σ Mx = 0; T = F·e;		τQy
Σ y = 0;	Qy = Fy;	Σ My = 0; My= Fz·x;
					τQz
Σ z = 0;	Qz = Fz;	Σ Mz = 0; Mz= Fy·x.	σ′
					τ	а
На выделенном элементе В (рис. 8.12, б) показаны			σ″
						T
действующие по его граням напряжения (рис. 8.13, а).
От поперечных сил и крутящего момента возникают ка-			σ′			б
сательные напряжения τQy, τQz, τT. От изгибающих мо-
ментов – нормальные напряжения σ′ и σ″. Для длинных			σ″	τT
валов и балок (ℓ > 10 d) влиянием поперечных сил часто			Рис. 8.13. Ана-
пренебрегают. Таким образом, учитывают только три			лиз напряжен-
момента: крутящий и два изгибающих. От них возника-			ного состояния

ют три напряжения: одно касательное и два нормальных (рис. 8.13, б).

Расчет на прочность при изгибе с кручением

Из рисунка 8.13, б следует, что в произвольном сечении возникает

плоское напряженное состояние

M y

σ

x

= σ

M z

+σ

M y

=

M

z

y +

z;

σ

y

= 0;

σ

z

= 0;

Iz

I y

τxz =

τT =

T

ρ.

I p

105

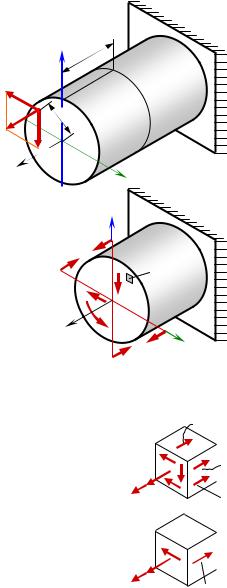
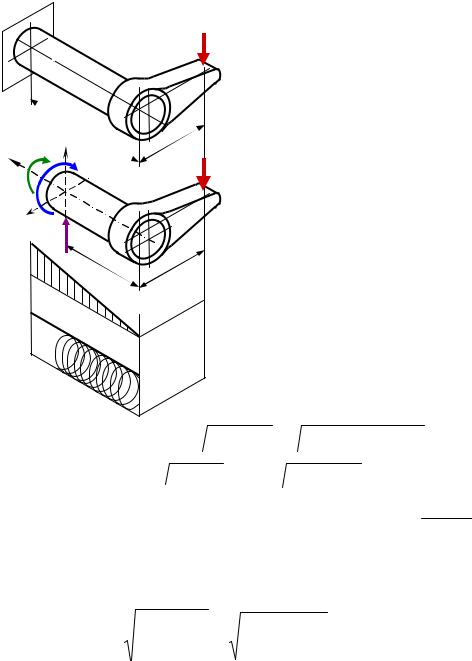
Как при изгибе, так и при кручении круглого сечения опасными являются точки на периферии. Для круга и кольца

Wz = Wy = Woc;

Wp = 2Woc.

σ

M y ,max

=

M y

;

σ

M z ,max

=

M

z

;

τ

T ,max

=

T

.

Woc

Woc

2Woc

Условие прочности для пластичных материалов по III теории проч-

ности (наибольших касательных напряжений):

σэкв = σ1 −σ3 ≤ [σ],

где

σ

=

σ

x +

σ

2

+ τ2 ;

σ

=

σ

x −

σ

2

x

3

x

+ τ2 .

1

2

2

xz

2

2

xz

Тогда

σ

экв

=

σx

+

1

σ

2

+ 4τ2

−

σx

−

1

σ

2

+ 4τ2

;

2

x

T

2

x

T

2

2

σэкв = σx2 + 4τT2 ≤ [σ].

Поскольку для круглого и кольцевого сечений не существует точки, одинаково удаленной от обеих осей инерции z, y, то используют результи-

рующий момент – геометрическую сумму векторов изгибающих моментов

относительно осей z, y:

	Мрез =		M 2y + M z2 .		(8.12)
Тогда	σx =	M рез		.
		Woc

σ

экв

=

M 2y + M z2

+4

T 2

≤ [σ], или σ

экв

=

M 2y + M z2 +T 2

≤ [σ].

W 2

(2W )2

Woc

oc

oc

Условие прочности при совместном действии изгиба и кручения:

σэкв =

M прив

≤ [σ].

(8.13)

Wос

Мприв – приведенный момент, действие которого эквивалентно совместному действию My, Mz, T в соответствии с используемыми теориями прочности.

По III теории прочности (наибольших касательных напряжений)

Мприв, III = M 2y + M z2 +T 2 .

(14)

По IV теории прочности (энергетической)

Мприв, IV = M 2y + M z2 +0,75 T 2 .

(15)

Приведенного момента в действительности не существует, изобразить его нельзя, вектора он не имеет. Величина приведенного момента за-

106

висит от используемой теории прочности. Результаты расчетов по III и IV теориям прочности близки, отличаются примерно на 5–10 %.

Пример 8.9. (Вольмир А. С. Сборник задач … 6.52). Вал с кривошипом подвергается действию силы F = 3,5 кН. Определить диаметр вала по третьей теории прочности при [σ] = 160 МПа; ℓ = 50 см, а = 10 см.

ℓ

xy T

Mz

z

F·ℓ Q x

F·a

		Решение. Внутренние усилия оп-
	F	ределяем методом сечений.
		Рассекаем вал на две части в произ-
	а	вольном сечении х,
		Отбрасываем одну из частей (поз. б ри-
	a	сунка),
		Заменяем действие отброшенной части
	F	внутренними усилиями и в коорди-
		натной системе xyz составляем

бУравнения статики:

	a	∑x = 0 ;	N = 0;	∑M x = 0 ;		T = -F·a;
		∑y = 0 ;	Qy = F; ∑M y = 0 ;			My = 0;
	в	∑z = 0 ;	Qz = 0;	∑M z = 0 ;		Mz = -F·x.
	Mz	Строим эпюры			изгибающего			и
		крутящего	моментов,		действующих			в
	г	поперечных сечениях вала (поз. в					и г
	T	рисунка).	Находим	приведенный			мо-
		мент в опасном сечении – в защемлении:

M прив = M z2 +T 2 = (− FA)2 + (− Fa)2 = = F A2 + a2 = 3500 0,52 +0,12 =1785 Нм.

Из условия прочности при изгибе с кручением σэкв = Mприв = [σ] находим

Wос

			W		= M прив = π d 3 ,
				ос			[σ]		32
откуда	d ≥ 3	32Mприв		= 3		32 1785				= 0,0484 м.
		π[σ]				π 160 106

Округлив до большего значения, принимаем диаметр вала d = 50 мм.

107

9. ДИНАМИЧЕСКОЕ ДЕЙСТВИЕ СИЛ

Нагрузка статическая – постоянная или изменяющаяся медленно так, что силами инерции вследствие ускорения, можно пренебречь.

Нагрузка динамическая – быстро меняющая свое значение или место приложения.

Метод расчета на динамическую нагрузку основан на принципе Даламбера: всякое движущееся тело можно рассматривать как находящееся в состоянии мгновенного равновесия, если к действующим на него внешним силам добавить силу инерции, равную произведению массы тела на его ускорение (J = a m), направленную в сторону, противоположную ускорению. Для определения динамических напряжений при ударе используют закон сохранения энергии.

9.1. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ ТЕЛА. ДИНАМИЧЕСКИЙ КОЭФФИЦИЕНТ

		Nдин			Пример. Груз Q поднимают с постоянным ускорени-
					ем а тросом с площадью поперечного сечения A, изготов-
A, γ					ленным из материала с объемным весом γ. Определить на-
			x		пряжение в тросе.
					Решение. Методом сечений определяем внутреннее
					усилие в произвольном сечении троса
				a		Q		a
Q					Nдин = Q + J = Q +	g	a = Q 1 +		,
								g

где g – ускорение свободного падения.

В покое статическое усилие Nст = Q. За счет движения с ускорением усилие возрастает в отношении

Кдин =	Nдин	=1 +	a	.	(9.1)
	Nст
			g

Отношение динамического значения некоторого фактора (усилия, напряжения, перемещения) к соответствующему статическому значению этого фактора называют динамическим коэффициентом.

Напряжение в тросе

			Q		a
σ	дин	=	1	+		.	(9.2)
			A		g

Если учитывать вес троса, то внутренние усилия в нем:

Nст = Q + γ A x.

Динамическое напряжение в тросе

	σдин =	Nдин	=	NстKдин	= σстKдин.	(9.3)
		A		A
				108

δдин

H

δx,дин

x

δx,ст

Условие прочности			σстКдин ≤ [σ].
σдин ≤ [σ]
Для нашего примера
Q					a		≤ [σ].
σдин =	A	+ γ x 1		+				(9.4)
					g

9.2. УДАРНОЕ ДЕЙСТВИЕ НАГРУЗКИ

Удар – взаимодействие тел, при котором за очень малый промежуток времени скачкообразно возникают конечные изменения скорости соударяемых тел.

Приняты следующие допущения:

удар неупругий, то есть тела после соударения не отделяются друг от друга и движутся совместно. После соударения в некоторый момент времени скорость перемещения ударяющего груза становится равной нулю;

вид деформированной системы (эпюра перемещений) при ударе в любой момент времени подобен виду деформированного состояния системы при статическом нагружении:

δх, дин	=	δдин	= Кдин ,
δх, ст
		δст

F

δст

Q= F

где δх, дин, δх, ст – динамический и статический прогиб в произвольном сечении х; δдин, δст – динамический и статический прогиб в точке соударения;

масса ударяемого тела считается малой по сравнению с массой ударяющего тела;

напряжения при ударе не превосходят предела пропорциональности так, что закон Гука при ударе сохраняет силу;

потерей части энергии, перешедшей в теплоту колебания, пренебре-

гают.

Динамический коэффициент без учета сил инерции ударяемого тела

Груз Q, падая с высоты Н, деформирует систему на δдин. Работа, совершаемая грузом Q на перемещении (Н+δдин)

W = Q(H + δдин).

109