КУРС сопромата с примерами

Для вала постоянной жесткости сечения (произведение G·Ip) на длине

ℓ и постоянного крутящего момента Т угол закручивания вала
ϕ =	T A	.	(5.8)
	G I p

Полученную зависимость называют законом Гука при кручении.

Произведение GIp называют жесткостью сечения при кручении.

5.5. РАСЧЕТ ВАЛОВ НА ЖЕСТКОСТЬ

За меру жесткости принимают относительный угол закручивания, то есть угол, приходящийся на единицу длины вала

θ = ϕA = G TI p .

Условие жесткости: θ = G TI p ≤ [θ],

где [θ] имеет размерность рад/м. Чаще пользуются условием

θ =	T	180D		≤ [θD].	(5.9)
	G I p		π

Допускаемое значение угла [θ°] закручивания зависит от назначения вала. Принимают [θ°] = (0,3–1,0) град/м.

При расчете валов на прочность и жесткость часто задают мощность N, передаваемую валом и частоту его вращения n. Для вычисления крутящего момента по этим данным удобно воспользоваться таблицей

M =	N					Вт = Н м
	ω					с−1
M =	N 30			= 9549 N		кВт		= Н м
	n	π				об/мин
				n
M =	N	30		N		кВт
				= 973,8 n				= кГ м
	n	π 9,807
						об/мин
M =	N 30 0,736			= 7028 N		л.с.		= Н м
	n	π				об/мин
				n
M =	N 30 0,736			N		л.с.		= кГ см
	n π 9,807			= 71620 n
						об/мин

60

Пример 5.1. Расчета вала на прочность и жесткость

M1

M2

Mвед

M3

Из условия прочности и жестко-

e

f

g

h

сти выполнить проектный расчет: оп-

ределить диаметры валов в двух вариан-

х

тах исполнения – сплошного и полого с

I

II

II

а

коэффициентом пустотелости с = d/D =

а

b

c

0,8.

Результаты

округлить

согласно

ГОСТу. Построить эпюры углов закру-

T,

+

чивания вала. Валы сопоставить по ме-

6

таллоемкости и жесткости.

кН м –0

б

Дано:

5

+

12

М1 = 5 кН·м;

a = 0,6 м;

βс 10–3

М2 = 7 кН·м;

b = 0,8 м;

0

в

–

3,14

М3 = 6 кН·м;

с = 0,7 м;

8,79

[σ] = 160 МПа;

[θ] = 0,8 град/м.

βп 10–3

+

13,19

0

г

–

3,12

I.

Определение внутренних

усилий

13,11

8,7

Значение

ведущего

момента

Рис. 5.3. Схема нагружения вала (а),

Мвед определим из условия

эпюра крутящих моментов (б), эпюры

равновесия вала: Σ Мх = 0;

углов закручивания сплошного (в) и

Мвед – М1 – М2

– М3 = 0,

откуда

полого (г) валов

Мвед

= М1 + М2 + М3 = 5 + 7 + 6 =

= 18 кН·м.

Для расчетов на прочность и жесткость необходимо найти положение опасных сечений и величины крутящих моментов, действующих в этих сечениях вала (рис. 5.3, а). Воспользовавшись методом сечений определим внутренние усилия и построим эпюру крутящих моментов (рис. 5.3, б). Опасными являются все сечения на участке II, где действует Тmax = 12 кН·м.

II. Проектный расчет валов сплошного и полого сечений

Предварительно найдем допускаемое касательное напряжение, связанное с допускаемым нормальным напряжением. Принимаем по третьей теории прочности

[τ] = 0,5 [σ] = 0,5·160 = 80 МПа.

Из условия прочности и жесткости при кручении находим требуемые значения полярных момента сопротивления и момента инерции

τ

= Tmax ≤ [τ],

W

≥ Tmax = 12000

= 0,00015 м3 =1,5 10−4 м3 .

max

Wp

p

[τ]

80 106

θ =

T

180D

≤ [θ],

I p ≥

T

180D =

12 000 180

=1,074 10−5 м4 .

G I p

π

G [θ]

80 109 0,8

π

π

61

62

Результаты расчетов

Форма сечения

Сплошное

Полое

Момент

Wp,спл

=

πD

3

Wp,пол =

πD

3

(1 −c4 )

сопротивления

16

16

16W

p

Dпол ≥ 3

16Wp

Диаметр

Dспл ≥ 3

;

;

π(1 − с4 )

π

из условия

= 3 16 1,5 10−4

Dпол ≥ 3 16 1,5 10−4

прочности

Dспл

= 0,0914 м

= 0,1090 м

π

π (1 − с4 )

Момент

πD4

= πD4 (1 −с4 );

инерции

Iспл

=

Iпол

требуемый

32

32

D

≥ 4

32 Iспл

;

Dпол ≥ 4

32 Iпол

;

Диаметр

4

спл

π

π(1 − с )

из условия

32 1,074 10−5

32 1,074 10−5

жесткости

Dспл

≥ 4

Dпол ≥ 4

π

= 0,1023 м

π(1 − 0,84 )

= 0,1167 м

Диаметр

Dспл = 105 мм

Dпол = 120 мм

согласно ГОСТ

Площадь

A

=

πDспл2

;

A

=

πDпол2

(1 − с2 );

поперечного

спл

4

пол

4

π

π

(1 − 0,8

)= 40,7 см

сечения

Аспл

2

2

Aпол =

2

2

2

=

4 0,105

= 86,6 см

0,120

4

62

Углы закручивания характерных сечений вала сплошного и полого сечений

Icпп

=

πD4

;

Iпол =

πD4

(1 − с4 );

Момент инерции

32

32

принятый

Iспл

=

π 0,105

4

=1,193 10−5 м4

Iпол =

π0,120

4

(1 − 0,84 )=1,202 10−5 м4

32

32

Жесткость

G·Ip = 80·109·1,19·10-5 = 0,955·106 Н·м2

G·Ip = 80·109·1,20·10-5 = 0,961·106 Н·м2.

сечения

T a

−5 103 0,6

T a

− 5 103 0,6

φI

=

I

=

0,955 106

= −0,00314;

φI

=

I

=

0,961 106

= −0,00312;

Углы

G I p

G I p

T b

−12 103 0,8

T b

−12 103 0,8

закручивания

φII

=

II

=

0,955 106

= −0,01005;

φII

=

II

=

0,961 106

= −0,00999;

G I p

G I p

участков вала

T c

6 103 0,7

T c

6 103 0,7

63

φIII

=

III

=

0,955 106

= 0,00440

φIII

=

III

=

0,961 106

= 0,00437

G I p

G I p

βспл,e =0.

βпол,e =0.

Углы

βспл, f

= φI =−3,14 10−3.

βпол, f

= φI =−3,12 10−3.

β

= φ + φ

=−(3,14+10,05) 10−3 =

β

= φ + φ

=−(3,12+9,99) 10−3 =

закручивания

спл,g

I

II

пол,g

I

II

характерных

−3

−3

сечений вала

=−13,19 10 .

=−13,11 10 .

βспл,h = φI + φII + φIII =

βпол,h = φI + φII + φIII =

=−(3,14+10,05−4,40) 10−3 =−8,79 10−3

=−(3,12+9,99−4,37) 10−3 =−8,74 10−3.

Строим эпюры углов закручивания сплошного и полого валов (рис. 5.3, в и г)

63

Результаты расчета валов

	Наружный диаметр вала, мм			2	Угол закручивания крайнего сечения
Поперечное сечение вала				Площадь поперечного сечения, мм
	Из условия прочности	Из условия жесткости	Принято по ГОСТу
Сплошное	91,4	102	105	8659	0,00879
Полое	109	116,7	120	4072	0,00874

III. Сопоставление металлоемкости валов двух вариантов

Металлоемкость вала определяется его объемом, то есть произведением длины на площадь поперечного сечения. Поскольку длина вала неизменна, сопоставим площади поперечных сечений сплошного вала с полым

А		(π 4)D2			1052
спл	=		спл	=				= 2,13 .
		(π 4)D2	(1−с2 )		1202
Апол							(1−0,82 )
		пол

Выводы:

1.Из условий прочности и жесткости найдены диаметры вала двух вариантов исполнения, сплошного и пустотелого: 105 и 120 мм соответственно.

2.Вычислены деформации валов на каждом из участков, построены эпюры углов закручивания валов сплошного и пустотелого. Жесткости валов практически одинаковы.

3.Сопоставлены металлоемкости валов двух вариантов исполнения. Расход металла для вала сплошного сечения вдвое больше, чем для вала пустотелого.

Примечание. Полученный ре-	τmax	τmax
зультат по сопоставлению металлоем-
кости валов ожидаем, поскольку доста-
точно большой объем материала, сосре-
доточенный около центра тяжести се-
чения, испытывает напряжения ниже
допускаемого и вклад его в общую

прочность конструкции невелик. Поэтому целесообразно убирать неработаю-

щий материал из этой области. Конструкции из полого сечения созданы природой: камыш, тростник, бамбук, злаковые культуры, трубчатые кости птиц и млекопитающих. В авиации и космонавтике используют полые валы, в строительстве – пустотные плиты перекрытий.

64

6. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ

При растяжении стержня напряжения во всех точках одинаковы, поэтому его напряженное состояние определяется внешней нагрузкой и площадью поперечного сечения, но не зависит от его формы.

В случае изгиба и кручения брусьев напряжения в точках поперечного сечения зависят от его формы и размеров, а при изгибе еще и от его ориентации к направлению нагрузок. Кроме площади сечение характеризуется:

статическим моментом площади; моментами инерции; радиусами инерции; моментами сопротивления.

У большинства характеристик физического смысла нет, но есть геометрическая интерпретация и аналогия с физическими и механическими понятиями.

	6.1. СТАТИЧЕСКИЙ МОМЕНТ ПЛОЩАДИ СЕЧЕНИЯ
y	dA	A	Статический момент площади – распро-
			страненная на всю площадь сумма произведений эле-

zментарных площадок dA на расстояние от них до этой оси

	y	z	Sz = ∫ y d A,	S y = ∫z d A.	(6.1)
	0
			A	A
	Рис. 6.1		Это понятие аналогично моменту силы относительно

оси. Если предположить, что А – вес пластины, имеющей форму нашего сечения, то статический момент Sz – это момент силы тяжести пластины относительно оси z. Размерность: единицы длины в третьей степени (см3; м3). Знаки: плюс, ноль и минус.

	Ось центральная – ось, относительно	y А				yC > 0
	которой статический момент площади равен		C			Sz > 0
	нулю.				C
					y
	Центр тяжести сечения – точка пере-	0	C			yC = 0
	сечения центральных осей.					z Sz = 0
	Если фигура имеет ось симметрии, то эта		А		C
					y
						yC < 0
	ось является центральной.		C
						Sz < 0
	Статический момент составного сечения
		Рис. 6.2. Связь знака стати-
	равен сумме статических моментов элементов
	этого сечения. Это следует из свойства опреде-	ческого момента площади
	ленного интеграла, который можно вычислять	с его положением в коор-
			динатной системе

по частям – свойство аддитивности (от англ.

add – прибавлять, присоединять, складывать). При известных статических

65

моментах частей сечения можно найти координаты центра тяжести состав-

ной фигуры:

zс =

S y

z

A + z

2

A +

+ z

n

A

yс

=

S

z

=

y

A + y

2

A +

+ y

n

A

A

= 1 1

2

n ;

1 1

2

n .

A1 + A2 + + An

A

A1 + A2 + + An

Пример 6.1. Определить положение центральных осей, параллель-

ных основанию и высоте фигуры.

Решение

Разбиваем сложную фигуру на две простые, в

Дано:

конкретном примере – на два прямоугольника. Их

H = 10 см;

h = 2 см;

центры тяжести расположены посредине высоты и

посредине ширины.

L= 8 см;

ℓ = 2 см.

Координаты центров тяжести

y

ℓ

и площади простых фигур

yС

z

= A = 2 =1 см;

1

2

2

С1

z2 = A+

L −A = 2 + 8

−2 = 5 см;

H

= H

2

2

С

zС

y

= 10 = 5 см;

1

2

2

1

С2

y2 = h = 2 =1 см;

y

C

h

y

2

2

A = A H = 2 10 = 20 см2;

z

1 z1

2

2

1

zC

y

A = (L −A)h = (8 −2)2 =12 см2.

2

z2

L

Статические моменты

площадей простых фигур

S

z1

= y A = 5 20 =100 см3; S

y1

= z A =1 20 = 20 см3;

1

1

1

1

S

z2

= y

2

A =1 12 =12 см3; S

y2

= z

2

A = 5 12 = 60 см3.

2

2

Координаты центра тяжести составной фигуры

zс =

S y1

+ S y2

=

20 +60

= 2,5 см; yс =

S

z1

+ S

z2

=

100 +12

= 3,5 см.

A1

+ A2

20

+12

20 +12

A1 + A2

Через найденную точку проводим центральные оси zC и yC, параллельные основанию фигуры и ее высоте.

Примечание. Центр тяжести фигуры, составленной из двух частей, лежит на линии, соединяющей центры тяжести простых фигур ее составляющих, причем расстояния до них обратно пропорциональны площадям

66

простых фигур. Если сложная фигура составлена из нескольких простых, то общий центр тяжести находится внутри многоугольника, вершинами которого являются центры тяжести простых фигур.

6.2. МОМЕНТ ИНЕРЦИИ СЕЧЕНИЯ

Момент инерции – распространенная на всю площадь сумма произведений элементарных площадок dA на квадраты расстояний от них до этой оси.

Осевые моменты инерции Iz = ∫ y2 d A,	I y = ∫z2 d A.	(6.2)
A	A
Полярный момент инерции I p = ∫ρ2 d A,		(6.3)
A

dA A

y1 y z

z1	y1 z1
ρ
0	y
	Рис. 6.2	z

где ρ – расстояние от площадки dA до точки (полюса), относительно которого вычисляется полярный момент инерции. Полярный момент инерции связан с осевыми моментами инерции

I p = ∫ρ2 d A= ∫(z2 + y2 )d A = ∫(z12 + y12 )d A,

A A A

то есть для любой пары взаимно перпендикулярных осей, проходящих через полюс 0

I p = Iz + I y = Iz1 + I y1 .

(6.4)

Центробежный момент инерции определяется интегралом произведений элементарных площадей на их расстояния до двух взаимно перпендикулярных осей

Izy = ∫z y d A.	(6.5)
A

Размерность моментов инерции – единицы длины в четвертой степени. Осевые и полярный момент инерции всегда положительны, центробежный момент инерции может принимать значения «+», «–» и ноль. Если фигура имеет ось симметрии, то относительно этой оси центробежный момент инерции равен нулю.

Пример 6.2. Найти моменты инерции прямоугольника относительно центральных осей, параллельных основанию и высоте.

Решение. dA – элементарная площадь; dA= b·dy.

	h 2	y3			h 2		b h3
Iz = ∫ y2 d A = ∫ b y2 d y = b						=		.
A	−h 2	3			−h 2	12

Аналогичное решение относительно оси у. Таким образом

y	dA
2	dy
h/	y
h/2	z
b
Рис. 6.3

67

Iz =	bh3	.	I y =	b3h	.	(6.6)
12			12

Пример 6.3. Найти моменты инерции круглого и кольцевого сечений.

Решение. Площадь элементарного кольца радиусом ρ и толщиной dρ: d A = 2πρ d ρ. Полярный момент инерции круга:

D 2

(D 2)4 = π D4 .

dA

y

I p = ∫ρ2 d ρ = ∫ 2πρ3 d ρ = 2π

A

0

4

32

dρ

ρ

Поскольку имеется связь I p = Iz + I y , а для круга

z

Iz = I y , то Iz = I y =

I p

.

2

D

Таким образом, полярный и осевые моменты инерции

круга

πD4

πD4

Рис. 6.4.

I p

=

,

Iz

= I y =

.

(6.7)

32

64

πD4

πd

4

πD4

d 4

d

Кольцо I

p

=

−

=

1 −

. Обозначая с =

– коэффициен-

32

32

32

D

4

D

том пустотелости, получим полярный и осевые моменты инерции кольца:

	I p =	πD4	(1 − с4 ),	Iz = I y =	πD4	(1 − с4 ).	(6.8)
		32			64

6.3. МОМЕНТ СОПРОТИВЛЕНИЯ

Момент сопротивления – отношение момента инерции к расстоянию до наиболее удаленной точки.

В расчетах на прочность при изгибе используют осевые моменты сопротивления

Wz

=

Iz

и Wy =

I y

.

(6.9)

ymax

zmax

Например, для прямоугольника

I y

b3h 2

b2h

W =

I

z

=

bh3 2

=

bh2

,

W

y

=

=

=

.

z

ymax

12 h

6

zmax

12 b

6

y

ymax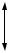

z

zmax

В расчетах на прочность при кручении сечений круглого профиля

	используют полярный момент сопротивления
	Wp =	I p	.	(6.10)
		ρmax

Так, для круга и кольца соответственно

68

Wp =

I p

=

πD4 2

=

πD3

. Wp =

I p

=

πD4 2

(1 −c4 )=

πD3

(1−c4 ).

32 D

16

32 D

16

ρmax

ρmax

Примечание. Для сечений некруглого профиля, например прямоугольного, моменты инерции и моменты сопротивления вычисляют по специальным формулам, включающим высоту и ширину профиля, а также коэффициент, зависящий от отношения высоты к ширине.

6.4. ЗАВИСИМОСТИ МЕЖДУ МОМЕНТАМИ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ

С – центр тяжести фигуры площадью А; оси z, y – центральные; a, b – расстояния между параллельными осями. Новые координаты для произвольной площадки dA:

y1 z1

b y z

C

A

0

Рис. 6.5

dA

a y

z

y1

z1 = z +b; y1 = y + a. I z1 = ∫ y12dA = ∫(y +a)2 d A;

A A

I z1 = ∫ y2 d A +2a ∫ y d A +a2 ∫d A.

A	A	A
I	II	III

Интеграл I – момент инерции фигуры относительно центральной оси; интеграл II – статический момент пло- z1 щади A относительно оси y равен нулю, поскольку эта ось является центральной;

интеграл III – площадь А фигуры.
Iz1 = Iz +a2 A; I y1 = I y +b2 A.	(6.11)

Момент инерции относительно произвольной оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.

Для центробежного момента инерции

Iz1y1 =I zy+a b A .

(6.12)

y	z		dA
y1
					y1
	z1
					z1
	α		y
0					z
y			B
y1					E z1
		D
					α
0	α				F
			C		z

6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ

Свяжем новые координаты z1, y1 элементарной площадки dA с координатами в исходной системе z, y:

z1 = 0E = 0D + DE = 0D + CF; y1 = BE = BF − EF = BF − DC.

Длины отрезков в исходной системе координат:

69