4.4 Понятие сетевого моделирования

Одним из важных преимуществ сетевого моделирования является возможность построения сетевых моделей, наглядно отображающие процессы коммерческой деятельности. Так, например, на рис. 4.4.1 представлен ориентированного графа движения денежных потоков на счетах бухгалтерского учета. Где в кружках указаны номера счетов бухгалтерского учет. А стрелками – проводки.

Значительное место в сетевом моделировании занимают задачи, связанные с планированием и составлением расписания выполнения работ или операций в коммерческой деятельности. В таких моделях множество работ всей совокупности задается отношениями предшествования между ними. Например, на рис 4.4.2 изображена сетевая модель комплекса работ по переводу торгового предприятия на самообслуживание.

. Обычно время и ресурсы выполнения каждой работы задается вначале. Кроме того, прежде чем работа может начаться , все ей предшествующие работы должны быть завершены. Например, доставка оборудования, событие 15 является предшествующей работой ( или Опорной) для работы по монтажу оборудования, Следовательно, при наличии полного перечня работ комплекса сеть можно построить, если точно установлены предшествующие для каждой работы. В таких случаях сетевая модель представляет собой отражение логической взаимосвязи всех входящих элементарных работ в комплексе от начала до конца. Сетевые графики представляют собой орггрфы без контуров, дугам и вершинам ( узлам) приписаны числовые значения, наибольшее распространение получил способ задания сетевых графиков в терминах дуги – операции, а вершины – события.

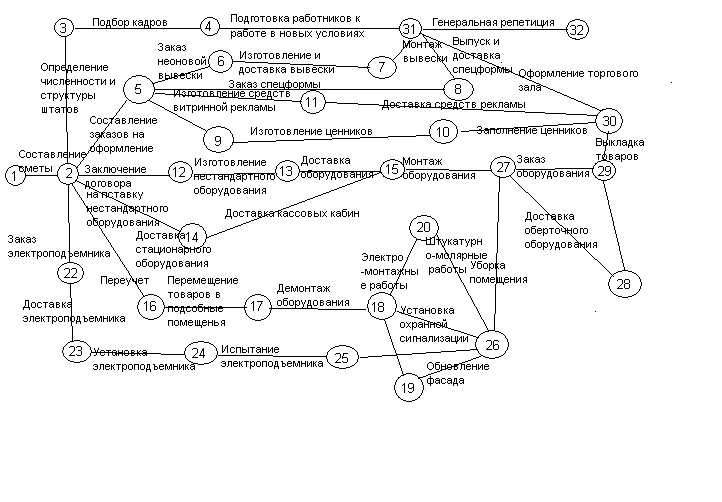
Исходное (1) – это такое событие, с которого начинается выполнение всего комплекса операций, а завершающее событие (32) соответствует достижению конечной цели, события обозначаются кружками, квадратами, ромбами, или другими геометрическими фигурами.

В сетевом моделировании различают следующие понятия:

1) фактическая работа (6, 7) изображена стрелкой(→), это процесс, требующий затрат ресурсов – времени, денег, людей, электроэнергии, товаров и т.д.;

2) работа – ожидание (—∙—∙→), это процесс, требующий только затрат времени, например ожидание, сушка, старение, затвердевание цементного раствора и т.п.;

3)критическая работа (), наиболее напряженная, нагруженная работа(13,15);

4) фиктивная работа(— — – →) обозначает логическую зависимость между работами (28,29), имеет нулевую продолжительность;

5) путь – любая непрерывная последовательность событий и работ;

6) критический путь – это, не имеющий резервов, включает только критические работы (1,2), (2,12), (12,13), (13,15), (15,27), (27,29), (29,30), (30,31), (31,32).

Приведенные определения, понятия и графические изображения являются основой методов сетевого планирования и управления, позволяющие проводить построение, анализ и оптимизацию сетевых моделей различных задач коммерческой деятельности.

4.5 Постановка сетевых задач коммерческой деятельности

4.5.1. Задача о максимальном потоке

Рассмотрим двухполюсную сеть S= (N,U) с одним входом (источником)sNи выходом (стоком)tN, дуги сети (i,j)Uимеют ограниченную пропускную способность

С. Задача о максимальном потоке заключается в поиске таких потоковпо дугам (i,j)cети, что результирующий поток из источника в сток является максимальным.

Математическая модель задачи о максимальном потоке выглядит следующим образом:

Найти такие значения , при которых

V =

при ограничениях:

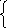0

.

Для решения этой задачи может быть использован метод построения увеличивающих цепей.

4.5.2. Задача о потоке минимальной стоимости

Пусть дана двухполюсная сеть S= (N,U)cисточникомsи стокомt.

Для каждой дуги (i,j)Uзадана пропускная способностьси стоимость доставки по ней единицы потокаr.Необходимо найти поток от источников в сток заданной величиныV, имеющей минимальную стоимость доставки. Очевидно, при этом величинаVне должна превышать максимального потокаV.

Математическая модель задачи имеет следующий вид:

4.5.3. Транспортная задача

Транспортная задача является одной из первых потоковых задач. Впервые была сформулирована и решена в 1941 г. Ф.Хичкоком и затем стала применяться в различных задачах перевозки и распределения. В этой задаче рассматриваются обычно как предложение грузов (товаров) от m-поставщиков в объёмах -и спрос отn-покупателей в объёмах -затраты на перевозку единицы груза отi- го поставщика кj-му покупателю составляют, а объёмы перевозимых грузов соответственно составляют, которые необходимо определить. Математическая модель имеет следующий вид.

Определить объёмы перевозок

___ ___

= ?i =1,m;j = 1,n ,

которые при условиях-ограничениях

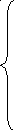
обеспечивали бы минимальные затраты на перевозку в соответствии с целевой функцией

Модель этой задачи может быть представлена в виде сети рис.4.5.1, если вершинам поставить в соответствие поставщиков и покупателей, а ориентированным дугам – дороги для перевозки грузов.

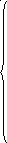
П

Р

Е

Д С

Л П

ОР

Ж О

Е С

Н

И

Е

Рис.4.5.1. Сетевая модель транспортной задачи

Эта задача является частным случаем задачи поиска потока минимальной стоимости. В то же время частным случаем транспортной задачи являются задачи о назначениях,

например задача оптимального распределения торговых агентов или маркетологов для изучения рынка по населённым пунктам.

4.5.4. Задача коммивояжера.

В коммерческой деятельности коммерсанты, торговые агенты постоянно проводят работу по поиску партнеров или клиентов для заключения договоров на поставку и покупку товаров. Для решения этих задач коммерсантам необходимо выезжать в командировки выполнять вояж по целой сети городов как по нашей стране, так и за рубежом. Поскольку продолжительность командировки и транспортные расходы следует сокращать, то необходимо составить кратчайший маршрут, предусматривающий посещение каждого пункта только один раз, и вернуться обратно. Задача коммивояжера заключается в определении такой последовательности объезда городов, которая обеспечит минимальное время переезда, или минимальную стоимость проезда, или минимальное расстояние переезда.

Постановка задачи. Пусть имеется nгородов. Расстояние между любой парой городов(i,j) известны и составляютгдеi=1,m; j=1,n; i≠j.Если прямого маршрута сообщения между городами не существует, а также для всехi=j полагаем, что= ∞. На этом основании расстояния между городами удобно представить в виде матрицыD= ().

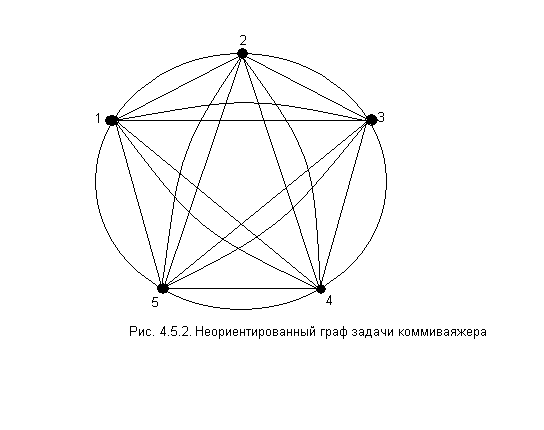
Если городам поставить в соответствие вершины графа (рис.4.5.2), а соединяющим их дорогам дуги, то в терминах теории графов задача заключается в определении гамильтонова контура минимальной длины. Гамильтоновым контуром называется путь, проходящий через все вершины графа, у которого начальная вершина совпадает с конечной, а длина контура определяется суммой длин всех дуг, входящих в контур. Таким образом, необходимо построить кольцевой маршрут проезда всех городов минимальной длины, начиная с любого пункта и в любую сторону.

Поскольку всего городов n, то коммивояжер, выехав из заданного города, должен побывать в остальных (n-1) городах только один раз. Следовательно, всего существует

(n-1)! Возможных маршрутов, среди которых один или несколько – оптимальные. В большинстве случаев можно предположить, что расстояние между городамиiиjявляется симметричным и равно расстоянию от городаjдо городаiявляется симметричным и равно расстоянию от городаjдо городаi, т.е.. Расстояние между городами запишем в виде матрицы и обозначим её черезD. Если в задачеnгородов, тоDявляется матрицей размером (nxn) с неотрицательными элементами, которые отображают длины дуг в сети городов. Приn= 5 количество возможных вариантов маршрутов равно (5 – 1)! = 24. Расстояние между городами заданы матрицей в табл.4.5.1.

Таблица 4.5.1.

i j	1	2	3	4	5
1 2 3 4 5	∞ 60 50 10 20	90 ∞ 30 70 40	80 40 ∞ 20 50	40 50 60 ∞ 20	100 70 20 50 ∞

Маршрут можно представить в виде замкнутого контура, представляющего собой кольцевой маршрут, например, для графа, изображенного на рис.4.5.2. Возможный вариант можно записать в виде совокупности соответствующих пар дуг:

М=.

Длина F( М) маршрута равна сумме соответствующих длин дуг матрицы расстояний, тогда целевую функцию можно записать так:

__ ____

i = 1,n; k = 1,(n-1)!

Для любого допустимого маршрута каждая строка и каждый столбец матрицы расстояний Dсодержат только по одному элементу. Решением задачи является определение кольцевого маршрута минимальной длины.

4.5.5. Распределение торговых агентов по городам

Торговая фирма продаёт товары в различных городах. В целях развития торговая фирма провела маркетинговые исследования в nгородах и установила покупательскую способность в каждом городе поусловных единиц. Затем фирма наняла на контрактной основеn торговых агентов для продвижения своих товаров на продажу в эти города. Профессиональный уровень агентов, конечно, различен и составляет долю реализуемых товаровi-тым агентом. Как распределить торговых агентов по городам, чтобы фирма получила максимальный доход от продажи товаров?

Введем управляющие переменные .

1, еслиiагент направлен вj-й город

= 0, в противном случае.

Введем параметр , который характеризует величину покупательных способностей, реализуемыхi-тым торговым агентом вj-том городе.

Математическая модель задачи имеет следующий вид.

__ __

Найти такие ,i= 1,n; j= 1,n, которые бы при условиях-ограничениях

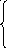
обеспечили бы максимальный доход от продажи в соответствии с целевой функцией

.

Первое и второе условие ограничений формализуют направление в каждый город по одному агенту.

Представленная математическая модель соответствует задаче о назначениях и может быть решена венгерским методом или методом потенциалов.

4.5.6. Формирование оптимального штата фирмы

Коммерческая фирма провела независимый анализ своей работы и установила профессиональную некомпетентность части сотрудников. Проведенные финансовые расчеты показали невыгодность обучения этих сотрудников. Фирма решила объявить конкурс на замещение вакантных должностей. Фирма провела отбор 300 человек из 15000 претендентов, поскольку считает, что обучение очень дорого.

В фирме n групп различных должностей: продавцов, кассиров, менеджеров, маркетологов, в каждой из которых повакантных единиц, . Претенденты проходили тестирование на профессиональную пригодность, по результатам которого их разделяли нат групп покандидатов в каждой группе, . Для каждого кандидата изi-й группы необходимы дополнительные затратына обучение для занятия j-й должности. Если= 0, претендент соответствует должности, а если= ∞, претендент не может вообще занимать рассматриваемую должность. Необходимо так распределить отобранных кандидатов по должностям, чтобы затраты на обучение были минимальными.

Математическую модель задачи можно записать так:

,

,

, ;

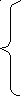
Решение этой задачи можно получить с помощью методов линейного программирования, в частности методов решения транспортной задачи . 4.5.7. планирование работ коммерческой деятельности

В коммерческой деятельности с целью исключения ущербов или неприятных неожиданностей необходимо составлять планы предстоящих работ, развернутых во времени. Обычно любое множество работ связано отношениями предшествования. Причем каждая работа может быть начата, если все предшествующие работы были завершены. В таких случаях сетевые методы позволяют решать как прямые, так и обратные задачи планирования работ коммерческой деятельности.

В результате решения прямых задач определяется оптимальный план комплекса работ при заданной схеме организации работ.

Решение обратной задачи связано с поиском оптимального плана схемы организации работ, обеспечивающего максимальную эффективность.

Множество возникающих задач коммерческой деятельности можно свести к одной из трех наиболее типичных постановок задач оптимизации.

1. Какое максимальное количество средств и каким образом может быть высвобождено при заданной организации работ при условии, чтобы общее время выполнения всего комплекса работ не возросло?

2. Как наилучшим образом использовать выделенные ограниченные ресурсы, чтобы время выполнения всего комплекса работ не превысило заданной величины?

3. Как распределить выделенные ресурсы между работами, чтобы время выполнения всего комплекса работ было бы минимальным?

При этом в исходных данных задач параметры работ могут быть заданы совершенно точно (детерминированный случай) или с некоторой степенью определенности, вероятности (стохастический случай).

Рассмотрим детерминированный вариант постановки задачи.

Подготовка задачи к решению начинается с формирования исходной информации на основе бесед со специалистами, детально представляющих специфику предстоящей работы. Например, специалист бухгалтерии могут пояснить движение денежных средств предприятия розничной торговли с указанием счетов и проводок бухгалтерского учета, что позволило построить ориентированный граф, представленный на рис. 4.5.3.

После описания содержания комплекса работ коммерческой деятельности следует выделить определяющие их характеристики. В качестве таковых могут быть:

В – общие ресурсы по выполнению комплекса работ;

- выделенные ресурсы для выполнения элементарной работы ( i j );

- длительность выполнения элементарной работы (i, j) выделенными рисунками ;

- коэффициент пересчета ресурса работы (i,j);

Т – время выполнения всего комплекса;

n – количество работ.

Затем проводят выбор главного экономического показателя, критерия эффективности, по которому определяют успех выполнения всего комплекса, например время выполнения работы Т или ресурсы В. В качестве критерия эффективности выбираем Т – время , которое необходимо найти минимальное из возможных .

В начале решения задачи рассматривается исходный вариант распределения общих ресурсов В по элементарным работам, что и определяет длительность их выполнения, поскольку известна связь.

Затем проводятся следующие операции:

а) составляется перечень всех работ, которые необходимо включить в сетевой график; б) указывается логическая очередность выполнения работ (предшествующие и последующие); в) определяются ресурсы для каждой работы, длительность их выполнения; г)определяются правилами пересчета ресурсов при их перераспределении между работами; д) все сведенья представляются в виде структурно-временной таблицы. Например, табл. 4.5.2 составлена для комплекса работ по переводу предприятия на самообслуживание.

Задача состоит в поиске минимального времени выполнения всего комплекса работ при заданных ограничениях в ресурсах В путем их оптимального перераспределения между работами.

На этом основании целевую функцию в обобщенном виде можно записать так:

Поскольку управляемыми параметрами являются ресурсы элементарных работ , определяющие длительность их выполнения , то необходимо найти новый вариант перераспределения выделенных ресурсов В путем переноса с одних работ (i, j) части ресурсов на другие работы (h, k), т.е. так, чтобы общий срок выполнения работ был минимальным из возможных.

Математическую модель задачи по переводу предприятия розничной торговли на самообслуживание можно представить таким образом:

найти такой вариант распределения ограниченных ресурсов В между элементарными работами

и такие неотрицательные значения длительности их выполнения

которые бы при заданных ограничениях

обращали бы в минимум функцию цели.

Решение задач этого класса может быть решено методами сетевого планирования, рассмотренными в разделе 4.6.3.