4.6 Методы решения сетевых задач

4.6.1. Построение максимального потока

На практике часто возникают задачи определения максимального количества товара, которое может быть перевезено от производителя потребителю. Аналогичными являются задачи определения максимальной пропускной способности системы автомагистралей, определения максимального количества нефти или газа, передаваемых по трубопроводам, информации, пропускаемой по компьютерной или телеграфной сети. Формально эти проблемы сводятся к задаче построения максимального потока в сети. Для решения необходимо ввести несколько понятий.

Пусть задана сеть S=(N, U) с множеством вершин N и множеством дуг U.

Определение.Дуга, соединяющая вершины сети S, называетсядопустимой дугой, если она обладает одним из следующих свойств:

1. направление дуги совпадает с направлением потока, и значением потока по этой дуге меньше её пропускной способности:

2. направление дуги противоположного направлению потока, и величина потока отлична от нуля:

Дуги, обладающие первым свойством, называют увеличивающими; дуги, обладающие вторым свойством, -уменьшающими.

Определение.Увеличивающие цепью, соединяющей вход и выход сети, называется простая цепь, все дуги которой являются допустимыми.

Пример. Построим увеличивающую цепь для сети S=(N,U), представленной на рис. 4.6.1.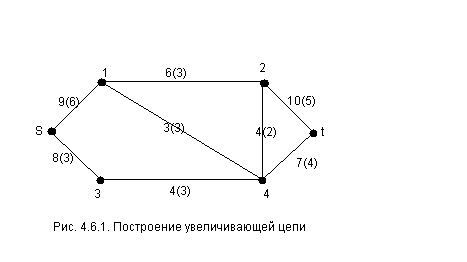

Над каждой дугой указана её пропускная способность, в скобках - поток по этой дуге.

Цепь (s, 1, 2, 4, t) является увеличивающей, так все её – допустимые:

- дуга (s, 1) – увеличивающая, так как она проходит по направлению потока, и поток по ней пропускной способности: 6<9;

- дуга (1, 2) – также увеличивающая дуга: 3<6;

- дуга (2, 4) – уменьшающая, так как она проходит против потока и поток по ней 2>0;

- дуга (4, t) – увеличивающая: 4<7.

Построим увеличивающую цепь для сети, представленной на рис.4.6.2. .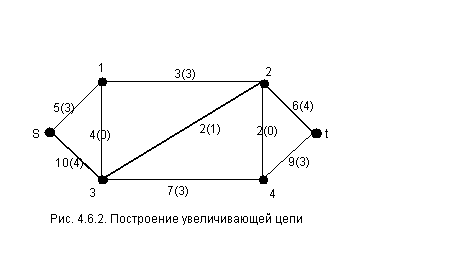

Цепь (s,3,2,t) – увеличивающая, так как все её дуги являются допустимыми увеличивающими дугами.

Определение максимального потока основано на увеличении потока вдоль увеличивающей цепи на величину.

Алгоритм построения максимального потока включает следующую последовательность:

1) задание начального значения потока. Удобно задавать нулевое значение;

2) построение увеличивающей цепи от входа к выходу сети. Если такой цепи нет, то максимальный поток построен, и его величина

в противном случае переходят к пункту 3;

3) увеличение вдоль построенной цепи значения потока на максимально возможную величину, при этом по каждой увеличивающей дуге уменьшается на.

Возврат к пункту 2.

Пример. Определим максимальный поток для сети (см. рис. 4.6.1). Начальный поток в сети задан, следовательно, пункт 1 алгоритма выполнен.

Увеличим поток вдоль цепи (s,1,2,4,t).

Вдоль дуги (s,1) поток можно увеличить на разницу между пропускной способностью этой дуги 9 и уже проходящим по ней потоком 6 ( 9 – 6 = 3 ).

Вдоль дуги (1, 2)аналогичным образом можно увеличить на 3 (6 – 3).

Дуга (2, 4) является уменьшающей. Максимальная величина, на которую можно уменьшить поток по ней, равна 2, т.е. значению уже проходящего потока.

По дуге (4, t) поток можно увеличить на 3 (7 – 4).

Таким образом, максимальная величина, на которую можно увеличить поток, составляет

При этом на каждой увеличивающей дуге поток увеличивается на эту величину, а по каждой уменьшающей – уменьшается.

Новое значение потока записано в скобках над дугой (рис. 4.6.3).

После такого перераспределения значение потока увеличилось на 2 и стало равным V = 11 (8+3 = 6 + 5), а условие сохранения потока в вершинах сети по-прежнему выполняется. Заметим, что если увеличить поток не на 2, а на 3, то по дуге (4,2) получим отрицательное значение -1 (2 – 3), что противоречит свойству неотрицательности потока.

Рассмотрим теперь цепь (s, 1, 2, t).

Эта цепь увеличивающая, так как все дуги – допустимые.

Поток вдоль этой цепи можно увеличить на

Новее значение потока указано на рис. 4.6.3.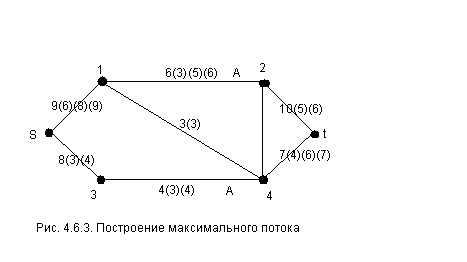

Заметим, что если увеличить поток на 5, то поток по дугам (s, 1) и (1, 2) превзойдет пропускную способность этих дуг.

Затем рассмотрим цепь (s,3,4,t):

Больше увеличивающих цепей нет, следовательно, максимальный поток построен. Его величина:

Минимальный разрез АА, соответствующий этому потоку, содержит дуги:{(1, 2); (1, 4); (3,4)}, а

его пропускная способность 6 + 3 + 4 = 13 соответствует величине максимального потока.

Из примера следует, что значение, на которое увеличивается поток вдоль увеличивающей цепи, определяется следующим образом:

Специалистам часто приходится изучать возможности сетей с незаданной жестко фиксированной ориентации, например, автомагистралей с двухсторонним движением с отсутствием сплошной разделительной полосы. Использование неориентированных сетей позволяет увеличить значение максимальных потоков по ним.

Построить максимальный поток в этом случае можно по следующему алгоритму:

1. заменить каждое ребро сети, не выходящее из источника и не входящее в сток, двумя противоположно направленными дугами, имеющими ту же пропускную способность, что и заменяемое ребро;

2. перейти к алгоритму построения максимального потока для ориентированной сети.

Пример. Построим максимальный поток для сети, представленной на рис. 4.6.4.

Начальное значение потока равно нулю V = 0.

Увеличивающие цепи:

Больше увеличивающих цепей построить нельзя.

Построим теперь максимальный поток для неориентированной сети с той же структурой рис. 4.6.5.

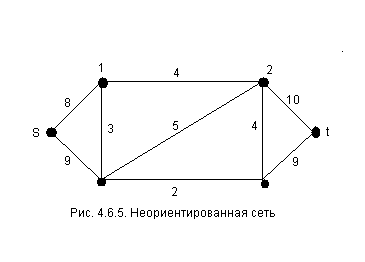
Заменяя ребра двумя противоположными направленными дугами, получаем следующую сеть рис. 4.6.6 .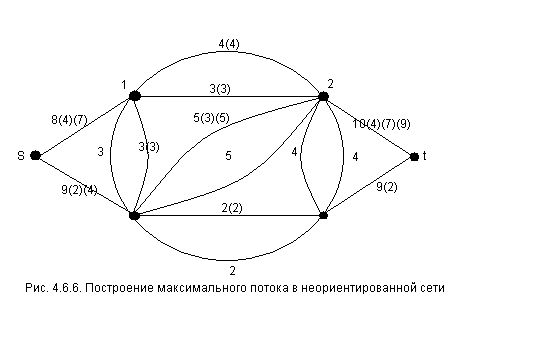

Увеличивающие цепи:

Больше увеличивающих цепей не существует. Максимальный поток . Оптимальная ориентация сети показана на рис. 4.6.7. .