
§ 4.12. Разрезы
Понятие разреза
играет важную роль при изучении вопросов,
связанных с отделением одного множества
вершин графа от другого. Такие задачи
возникают, например, при изучении потоков
в сетях (сетью
называется
связный орграф G=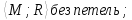 потоком
в сети G
называется функция
потоком
в сети G
называется функция
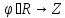 ,
которая ставит в соответствие дуги
некоторое число- вес дуги). В этих задачах
фундаментальную роль играют изучение
поперечных сечений сети (т.е. множеств
дуг, которые соединяют вершины двух
непересекающихся множеств вершин) и
нахождение ограниченного поперечного
сечения, которое является самым узким
местом. Эти узкие места определяют
пропускную способность системы в целом.
,
которая ставит в соответствие дуги
некоторое число- вес дуги). В этих задачах
фундаментальную роль играют изучение
поперечных сечений сети (т.е. множеств
дуг, которые соединяют вершины двух
непересекающихся множеств вершин) и
нахождение ограниченного поперечного
сечения, которое является самым узким
местом. Эти узкие места определяют
пропускную способность системы в целом.
Пусть G=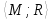 -
неорграф
-
неорграф
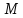 =
=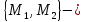 разбиение множестваM.
Разрезом
графа G
(по разбиению
разбиение множестваM.
Разрезом
графа G
(по разбиению
 )
называется множество всех ребер,
соединяющих вершины изM1
с вершинами из M2
(рис. 4.46). Отметим, что в связном графе
любой разрез непуст.
)
называется множество всех ребер,
соединяющих вершины изM1
с вершинами из M2
(рис. 4.46). Отметим, что в связном графе
любой разрез непуст.
Непустой разрез
K
неорграфа G
называется простым
разрезом
или коциклом,
если любое непустое собственное
подмножество K̕ K
не является разрезом ни по какому
разбиению. Другими словами, из K
нельзя удалить ни одно ребро с тем,чтобы
множество было непустым разрезом.
K
не является разрезом ни по какому
разбиению. Другими словами, из K
нельзя удалить ни одно ребро с тем,чтобы
множество было непустым разрезом.






M₁ Разрез M₂
рис. 4.46
Теорема 4.12.1.
В конечном
неорграфе G=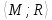 ,
имеющем с компонент связности, множество
ребер K
тогда и только тогда является коциклом,
когда граф
,
имеющем с компонент связности, множество
ребер K
тогда и только тогда является коциклом,
когда граф
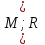 имеет (c+1)
компонент связности.
имеет (c+1)
компонент связности.
Понятие остова и коцикла являются противоположными в том смысле, что остову соответствует минимальное множество ребер, которые связывают посредством маршрутов все вершины связного графа, а коцикл состоит из минимального множества ребер, отделяющего некоторые вершины связного графа от остальных.
Следующие две почти очевидные теоремы дают информацию о связи остовов с разрезами, а также циклов с разрезами.
Теорема 4.12.2. В связном неорграфе остовное дерево имеет по крайней мере одно общее ребро с любым из разрезов графа.
Теорема 4.12.3. В связном неорграфе любой цикл имеет с любым разрезом четное число общих ребер.
В условиях,
указанных в предыдущем параграфе,
рассмотрим неорграф G
с остовом T.
Снова пусть
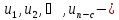 ветви
остоваT.
Удаляя из остова T
произвольную ветвь
ветви
остоваT.
Удаляя из остова T
произвольную ветвь
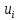 ,
получаем лесc(c+1)
компонентами связности, т.е. каждое
ребро
,
получаем лесc(c+1)
компонентами связности, т.е. каждое
ребро
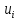 является разрезом остоваT
по некоторому разбиению
является разрезом остоваT
по некоторому разбиению
 ( рис. 4.47).
( рис. 4.47).






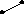

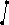
M₁ M₂
рис. 4.47
В графе G
могут найтись еще какие-то ребра
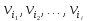 ( являющиеся хордамиT),
которые соединяют вершины из
( являющиеся хордамиT),
которые соединяют вершины из
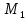 и
и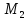 .
Множество
.
Множество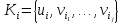 образует простой разрез, который
называетсяфундаментальным
разрезом
графа G
относительно ветви
образует простой разрез, который
называетсяфундаментальным
разрезом
графа G
относительно ветви
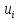 остоваT.
Множество
остоваT.
Множество
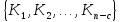 всех фундаментальных разрезов графаG
называется фундаментальным
множеством коциклов
графа G
относительно остова T.
Отметим, что мощность фундаментального
множества коциклов не зависит от выбора
остова T
и равна корангу
всех фундаментальных разрезов графаG
называется фундаментальным
множеством коциклов
графа G
относительно остова T.
Отметим, что мощность фундаментального
множества коциклов не зависит от выбора
остова T
и равна корангу
 *
*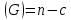 .
.
Аналогично
фундаментальным циклам каждому
фундаментальному разрезу
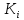 ставится в соответствие вектор
ставится в соответствие вектор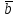 i
i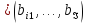 ,
определяемый по правилу
,
определяемый по правилу
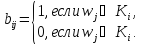
Фундаментальное
множество коциклов задается матрицей
фундаментальных разрезов
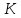 ,
строки которой являются векторами
,
строки которой являются векторами
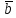 1,
1,
 2,
… ,
2,
… ,
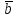 v*(G):
v*(G):
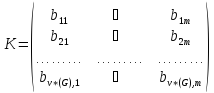 .
.
Поскольку
каждый фундаментальный разрез
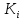 содержит ровно одну ветвь, а именно
содержит ровно одну ветвь, а именно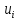 ,
матрица
,
матрица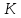 имеет вид
имеет вид
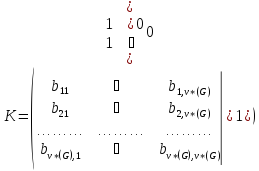 .
.
Таким
образом, K=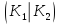 ,
где
,
где
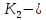 единичная
матрица порядка
единичная
матрица порядка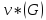 .
Отметим, что еслиC=
.
Отметим, что еслиC=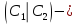 соответствующая
матрица фундаментальных циклов, то
соответствующая
матрица фундаментальных циклов, то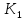 =CT2.
=CT2.
П р и м е р 4.12.1.
Найдем матрицу фундаментальных разрезов
графа G=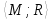 ,
изображенного на рис. 4.45. Поскольку
,
изображенного на рис. 4.45. Поскольку
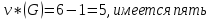 фундаментальных
разрезов. Ребру 4 соответствует коцикл
фундаментальных
разрезов. Ребру 4 соответствует коцикл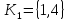 ,
так как при удалении ребра 4 из остоваT
множество вершин M
разбивается на две части∶
,
так как при удалении ребра 4 из остоваT
множество вершин M
разбивается на две части∶
 иM\
иM\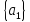 ,
а ребра 1 и 4 образуют разрез по разбиению
,
а ребра 1 и 4 образуют разрез по разбиению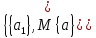 .
Аналогично ребру 5 соответствует коцикл
.
Аналогично ребру 5 соответствует коцикл ,
ребру 6-коцикл
,
ребру 6-коцикл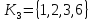 ,
ребру 7-коцикл
,
ребру 7-коцикл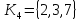 ,
ребру 8-коцикл
,
ребру 8-коцикл .
Следовательно, матрица фундаментальных
разрезов имеет вид
.
Следовательно, матрица фундаментальных
разрезов имеет вид
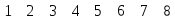
 .
.
