§ 4.15. Планарные графы.
Неорграф G называется планарным, если его можно изобразить на плоскости так, что никакие два ребра не будут иметь общих точек, кроме, может быть, общего конца этих ребер. Такое изображение графа на плоскости называется плоским. Таким образом, если граф имеет плоское изображение, то он является планарным.
П р и м е р
4.15.1. Граф
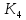 ( рис. 4.48а) планарен, поскольку может
быть изображен, как показано на рис.
4.48б.
( рис. 4.48а) планарен, поскольку может
быть изображен, как показано на рис.
4.48б. 


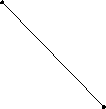


а б
рис. 4.48
Граф, описанный в примере 4.14.2,п.2, является планарным. Также планарным является граф, вершины которого –отверстия печатной платы, а ребра-проводники печатной платы, соединяющие отверстия.
Рассмотрим
операцию подразбиения
ребра в графе
G=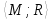 .
После подразбиения ребра
.
После подразбиения ребра
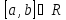 получается графG̕=
получается графG̕=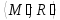 ,
где
,
где
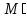 =
=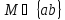 ,R̕=
,R̕=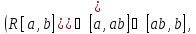 т.е. ребро
т.е. ребро
 заменяется на
заменяется на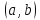 -
цепь длины два. Два графа называютсягомеоморфными,
если их можно получить из одного графа
с помощью последовательности подразбиений
ребер.
-
цепь длины два. Два графа называютсягомеоморфными,
если их можно получить из одного графа
с помощью последовательности подразбиений
ребер.
Не всякий неорграф является планарным. Критерий планарности описывает
Теорема 4.15.1 ( теорема Понтрягина-Куратовского).
Граф G планарен тогда и только тогда, когда G не содержит подграфа, гомеоморфного K5 или K3,3 ( рис. 4.49).





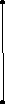
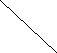





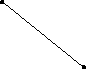

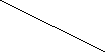






K₅K₃,₃
рис. 4.49
Эквивалентная форма критерия планарности описана в следующей теореме.
Теорема 4.15.2. Тогда и только тогда неорграф G планарен, когда G не содержит подграфов, стягиваемых (т.е. получаемых последовательностью отождествлений вершин, связанных ребрами) к графу K5 или K3,3 ( рис. 4.49).
Вместе с тем трехмерного евклидова пространства оказывается достаточно для изображения любого конечного и счетного графа без пересечения дуг вне их концов.
Теорема 4.15.3. Любой
граф ,состоящий
не более чем из
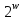 вершин, может быть изображен в пространстве
вершин, может быть изображен в пространстве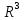 без пересечения дуг вне их концов.
без пересечения дуг вне их концов.
Д о к а з а т е л
ь с т в о. Пусть
G=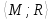 - граф, для которого
- граф, для которого
 . Расположим все
точки графа G
на некоторой
прямой
. Расположим все
точки графа G
на некоторой
прямой
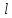 и каждой дуге
из
и каждой дуге
из
 разнозначно
сопоставим плоскость,
содержащую прямую
разнозначно
сопоставим плоскость,
содержащую прямую .
Искомое изображение графаG
получается после проведения всех дуг
в соответствующих плоскостях.
.
Искомое изображение графаG
получается после проведения всех дуг
в соответствующих плоскостях.
Известна оценка хроматического числа планарных графов.
Теорема 4.15.4
(теорема о четырех красках). Если G-
планарный граф, то χ(G)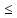 4.
4.
При исследовании
принципиальной электрической схемы
радиоэлектронного устройства с точки
зрения возможности ее реализации с
помощью печатного монтажа или монтажа
на слоях микросхемы важно знать ответ
на следующие вопросы: 1) является ли
граф, соответствующий рассматриваемой
принципиальной схеме, планарным? 2) если
граф планарен, то как получить его
изображение без пересечения ребер? На
первый вопрос принципиальный ответ
дает теорема Понтрягина-Куратовского,
а методы получения плоских изображений
планарных графов можно найти в книге
Б.Н. Деньдобренко, А.С. Малика
 .
.
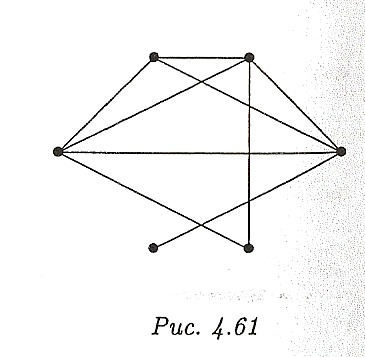
Если граф G непланарен, то для его геометрической реализации удаляют отдельные ребра ( переносят на другую плоскость). Минимальное число ребер, которое необходимо удалить из графа для получения его плоского изображения, называется числом планарности графа G. При вынесении этих ребер на вторую плоскость получают часть графа, которая также может оказаться неплоской. Тогда вновь решают задачу вынесения отдельных ребер на следующую плоскость и т.д. Минимальное число плоскостей m, при котором граф G разбивается на плоские части G1, G2, … , Gm (разбиение ведется по множеству ребер) , называется толщиной графа G.
Таким образом, толщина планарного графа равна 1.
П р и м е р 4.15.2. Каждый из графов K5 и K3,3 имеет толщину 2.
Задачи и упражнения
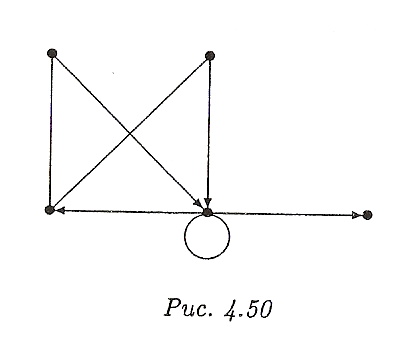
Представить граф ( рис. 4.50) в аналитической и матричной формах, списком дуг и структурой смежности.
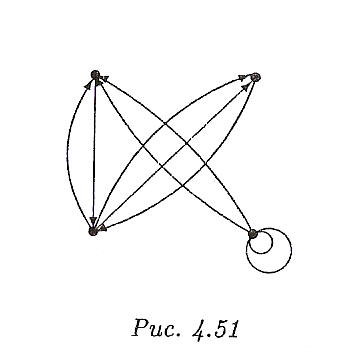
Составить матрицу инцидентичности для мультиграфа, изображенного на рис 4.51.
Найти все неизоморфные подграфы и части графа K3.
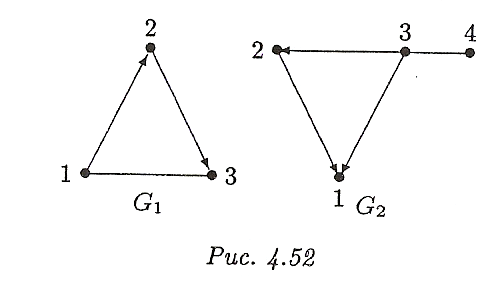
Представить в геометрической и матричной формах графы
 (рис. 4.52)
(рис. 4.52)
Для графов G1 и G2 из предыдущей задачи найти
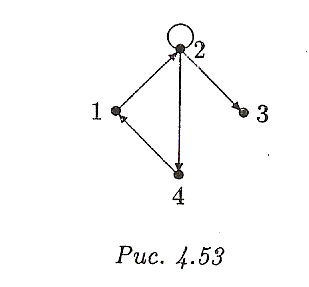
C помощью матрицы смежности графа ( рис. 4.53) найти его матрицы достижимости, контрдостижимости и сильных компонент.
Найти матрицу расстояний, диаметр, радиус, центральные и переферийные вершины графа, изображенного на рис. 4.54.

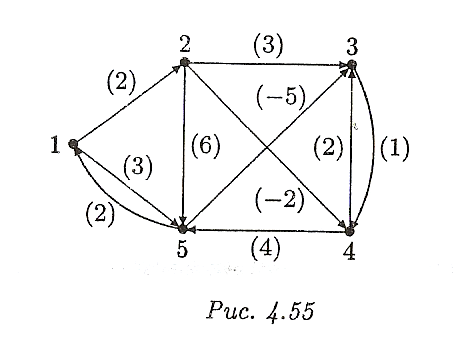
Найти все кратчайшие маршруты из вершины 2 для взвешенного графа ( рис. 4.55).
Доказать, что в любом конечном бесконтурном графе существуют вершины с нулевой полустепенью исхода и с нулевой полустепенью захода.
Проверить на эйлеровость и найти минимальное множество покрывающих цепей: а) графа K5; б) графа, изображенного на рис. 4.56.

Построить все неизоморфные трех-,четырех- и пятивершинные деревья.
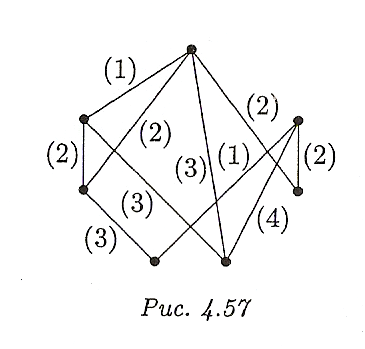
Найти остов минимального веса взвешенного графа ( рис. 4.57).
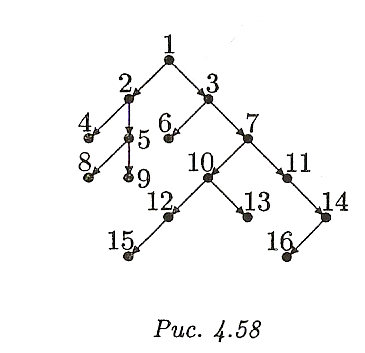
Найти упорядоченный лес, соответствующий бинарному дереву, изображенному на рис. 4.58.
Найти матрицы фундаментальных циклов и фундаментальных разрезов графа ( рис. 4.59).
Найти хроматическое число графа ( рис. 4.60).

Найти толщину графа. ( рис. 4.61).