
§ 4.14. Раскраски графов
Пусть G=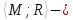 неорграф
без петель. Раскраской
(вершин)
графа G
называется
такое задание цветов вершинам G,
что если
неорграф
без петель. Раскраской
(вершин)
графа G
называется
такое задание цветов вершинам G,
что если
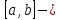 ребро,
то вершины
ребро,
то вершины
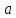 и
и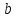 имеют различные цвета.Хроматическим
числом χ(G)
графа G
называется минимальное число цветов,
требующееся для раскраски G.
имеют различные цвета.Хроматическим
числом χ(G)
графа G
называется минимальное число цветов,
требующееся для раскраски G.
П р и м е р 4.14.1.
Так как в полном графе Kn
любые две различные вершины связаны
ребром, то χ(Kn)=n.

Многие практические задачи сводятся к построению раскрасок графов.
П р и м е р 4.14.2 1. Рассмотрим задачу составления расписания. Предположим, что нужно прочесть несколько лекций за кратчайшее время. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно ( например, их читает один и тот же лектор). Построим граф G, вершины которого биективно соответствует лекциям и две вершины смежны тогда и только тогда, когда соответствующие им лекции нельзя читать одновременно. Очевидно, что любая раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам одного цвета, могут читаться одновременно. Напротив, любое допустимое расписание определяет раскраску графа G. Оптимальные расписания соответствуют раскраскам с минимальным числом цветов, а число часов, необходимое для прочтения всех лекций, равно χ(G).
2.Рассмотрим
граф G,
вершины
которого-страны, а ребра соединяют
страны, имеющие общую границу. Числу
χ(G)
соответствует наименьшее число красок,
необходимых для раскраски карты так,
чтобы никакие две соседние страны не
были окрашены в один цвет. 
Существуют и практические задачи, связанные с раскраской ребер в мультиграфе.
Раскраска ребер
в мультиграфе G
может быть определена с помощью раскраски
вершин так называемого реберного
мультиграфа L(G).
Для произвольного неориентированного
мультиграфа G=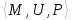 реберным
мульграфом
L(G)
называется тройка
реберным
мульграфом
L(G)
называется тройка
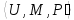 ,
где
,
где
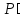
 U
U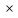 M
M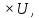 и выполняется
и выполняется
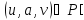 тогда и только тогда, когда в мультиграфеG
вершина
тогда и только тогда, когда в мультиграфеG
вершина
 является концом ребер
является концом ребер
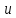 и
и .Раскраской
ребер мультиграфа
G
называется раскраска вершин мультиграфа
L(G).
.Раскраской
ребер мультиграфа
G
называется раскраска вершин мультиграфа
L(G).
П р и м е р 4.14.3.
Проводится монтаж аппаратуры. Чтобы не
перепутать проводники , необходимо их
окрасить таким образом, чтобы два
проводника, идущие к одной плате, имели
разные цвета. В этом случае вершинами
являются платы, а ребрами- проводники.

Неорграф G
называется бихроматическим,
если χ(G)=2.
Неорграф G=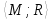 называется
двудольным,
если множество всех ребер графа G
образует разрез графа G,
т.е. для некоторого разбиения множества
вершин
называется
двудольным,
если множество всех ребер графа G
образует разрез графа G,
т.е. для некоторого разбиения множества
вершин
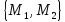 концы любого ребра принадлежат разным
частям разбиения.
концы любого ребра принадлежат разным
частям разбиения.
Теорема 4.14.1. Пусть G-неорграф без петель, имеющий хотя бы одно ребро. Тогда следующие условия эквивалентны:
G-бихроматический граф;
G-двудольный граф;
G не содержит циклов нечетной длины.
Следствие
4.14.2. Если
G-лес,
то χ(G)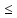 2.
2.
Оценим хроматическое число графа G через его параметры. Обозначим через deg(G) максимальную степень вершин графа G.
Теорема 4.14.3.
Для любого
неорграфа G
без петель выполняется неравенство
χ(G)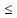 deg(G)+1.
deg(G)+1.
Рассмотрим простой алгоритм построения раскраски, который во многих случаях приводит к раскраскам, близким к минимальным.
Алгоритм последовательной раскраски.
Произвольная вершина
 графа G
принимает цвет 1.
графа G
принимает цвет 1.Если вершины
 раскрашены
раскрашены
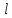 цветами 1,2, … ,
цветами 1,2, … ,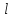 ,
,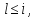 то
новой произвольно взятой вершине
то
новой произвольно взятой вершине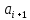 припишем минимальный цвет, не
использованный при раскраске вершин
из множества
припишем минимальный цвет, не
использованный при раскраске вершин
из множества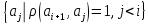 .
.
Для некоторых классов графов последовательная раскраска является минимальной. В общем случае это не так.
