Методические указания по выполнению расчетно-практи- ческой работы составлены в соответствии с программой курса математики и имеют своей целью выработать у студентов практические навыки решения задач математической статистики. Составлены из кратких теоретических сведений, примеров выполнения заданий и подбора заданий для самостоятельного решения.

1. Указания по выполнению первого задания:

Статистическая оценка параметров распределения. Гистограмма. Доверительный интервал

1.1. Краткие сведения, необходимые для выполнения работы

При конкретных практических исследованиях в распоряжении имеется ограниченное число реализаций случайной величины X, образующих выборочную совокупность (выборку). По выборке можно вычислить оценки соответствующих статистических характеристик генеральной совокупности. Выборка представляется простым статистическим рядом. Обычно такой ряд оформляется в виде табл. 1.1, в первой строке которой стоит номер опыта, а во второй – реализации случайной величины.

Таблица 1.1

i	1	2	3	…	n
xi	x1	x2	x3	…	xn

Состоятельные несмещенные оценки математического ожидания (выборочное среднее mx) и дисперсии (исправленная

выборочная дисперсия σ2x ) имеют следующий вид

~

=

1

n

(1.1)

mx

n

∑xi ,

i=1

~2

1

n

~

2

n

~

~ 2

σx

=

∑(xi

−mx ) =

(mx2

−(mx )

).

(1.2)

n −1

n −1 i=1

Эти формулы могут быть использованы для непосредственного расчета по данным простого статистического ряда. Расчет становится громоздким при большом объеме выборки n. В этом случае выборку удобнее оформлять в виде статистического (вариационного) ряда.

При этом выборка преобразуется следующим образом:

а). Весь диапазон изменения [xmin, xmax] случайной величины X делится на к интервалов, где к приближенно можно выбрать по формуле

к = 1 + 3,2lgn

(1.3)

с округлением до ближайшего целого. Длины всех интервалов выбираются равными

= (xmax − xmin ) / к

(1.4)

б). Подсчитывается mi(1≤ i ≤ к) – число реализаций случайной величины, попавших в i-й интервал. Если значение xi попадает на границу внутри диапазона (изменения Х) между i-м и (i+1)-м интервалами, то рекомендуется к mi и mi+1 прибавить по ½ или 1 к одному из них (так как с точки зрения статистики при больших объемах выборки это не принципиально). Определяется относительная частота, соответствующая каждому интервалу

P* = mi ,1 ≤i ≤ к		(1.5)
i	n

в). Статистический (вариационный) ряд оформляется в виде табл. 1.2

						Таблица 1.2
X	(x1;x2)	(x2;x3)	…	(xi;xi+1)	…	(xk;xk+1)
Mi	m1	m2	…	mi	…	mk
Pi*	P1*	P2*	…	Pi*	…	Pk*

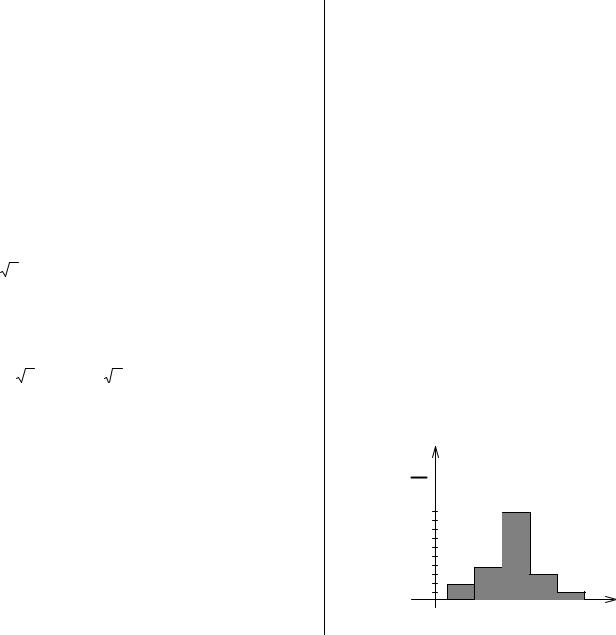
Этот ряд также может оформляться и графически в виде гис-
тограммы. Гистограмма изображается в виде прямоугольников,
			площадью		равной		отно-
	Pi *		сительной		частоте			Pi*
			соответствующих			интерва-
			лов (рис. 1).
			Замечание.			Количест-
			во интервалов, их длины, а
			также масштаб могут изме-
			няться	в	зависимости			от
x1	x2Рисx.31. Гистограмма… xk+1	x	решаемых задач.
			По		построенному
			статистическому			(вариаци-

онному) ряду несмещенная оценка математического ожидания (выборочное среднее) может быть вычислена как:

~		1		k		к	*
mx	=			∑xi mi =		∑xi Pi		,	(1.6)
			n
				i=1		i=1
где xi = (xi+1 + xi ) / 2 – середина i-го интервала, i=1,2,…,k.
		~		~	+ ε2 )	называется			доверительным
Интервал Iβ = (a				−ε1 ;a

интервалом с доверительной вероятностью β, если выполняется

соотношение		~
~	−ε1		+ε2 )=β,	(1.7)
P(a		< a < a
где a – точное значение некоторого параметра;				~
				a – оценка па-

раметра; ε1 ,ε2 – искомые числа.

Построение доверительного интервала для mx при неизвестной дисперсии основано на том, что величина

		~	− m x
Τ =		m x			(1.8)
	n		~
			σx

распределена по закону Стьюдента с ν=n−1 степенями свободы. По табл. 1 приложения для ν = n −1 и уровня значимости

	q можно найти такое tкр, что интервал							~
	~		~		~
			σx					σx		(1.9)
	I β = m x	− tkp		,	m x	+ tkp
			n					n

будет доверительным интервалом, соответствующим доверительной вероятности β.

Построение доверительного интервала для σx2 основано на том, что величина (n −1)σ~2x 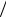σ2x распределена по закону χ2 (хи – квадрат) с ν=n–1 степенями свободы. Величина q называется уров-

нем значимости критерия проверки
	q =1−β.					(1.10)
По табл. 2 приложения для ν=n–1 и вычисленным по дан-
ному значению q вероятностям
P1	= 1 − q / 2,		P2	= q / 2		(1.11)
можно найти такие числа χ12 ,χ22 , что интервал
	~ 2			~ 2
	(n −1) σx	;	(n −1) σx			(1.12)
	2			2
Iβ =
	χ2			χ1

будет доверительным интервалом для σx2, соответствующим доверительной вероятности β.

1.2. Пример выполнения первого задания Произведено 20 независимых наблюдений над случайной

величиной Х, характеризующей отклонение длины детали от требуемой по техническим условиям. Результаты опытов представлены в виде простого статистического ряда:

i	1	2	3	4	5	6	7	8	9	10	11	12	13
xi	1	9	6	15	6	12	3	12	10	11	16	10	5
i	14	15	16	17	18	19	20
xi	11	11	7	12	14	21	12

Необходимо построить статистический (вариационный) ряд и гистограмму, найти оценки для математического ожидания и дисперсии, построить соответствующие доверительные интервалы для β = 0,95.

1.2.1. Преобразуем выборку в форму статистического (вариационного) ряда.

Здесь, используя (1.3),(1.4) k=1+3,2 lg20=1+3,2 1,3≈5,16≈5; = (xmax − xmin ) / 5 = (21−1) / 5 = 4 .

Найдем mi и Pi*. Для этого сформируем интервалы (mi – число попаданий в интервал). Результаты сведем в табл. 1.3.

							Таблица 1.3
Х			[1;5)	[5;9)	[9;13)	[13;17)	[17;21]
mi			2	4	10	3	1
Pi*=	mi		0,1	0,2	0,5	0,15	0,05
	n

Построим

гистограм-

Pi *

му (см. рис. 2).

~

~2

1.2.2. Вычислим mx

и

, используя (1.1),(1.2):

0,125

σx

~

= 3 0,1 + 7 0,2 + 11 0,5 +

mx

+15 0,15 + 19 0,05 = 10,4.

~2

20

2

2

2

0,0125

σx

= 19 (3

0,1 +7

0,2 +11

1

5

9

13

17

21

x

0,5 +152 0,15 +192 0,05 −

Рис.2

	2	)=	20	(123−108,16)≈15,621. Тогда	~
−(10,4)			19		σx	= 15,621 ≈ 3,952 .

1.2.3.Построим доверительный интервал для mx:

ν= n–1 = 20 – 1 = 19; β=0,95; tkp≈2,09 (по табл.1 прилож.).

Тогда, согласно (1.7)-(1.9)

~

~

~

~

σx

σx

I

= m

−t

;m

+t

;

n

β

x

kp

x

kp

n

				15,621			15,621
Iβ =		10,4	−2,09		;10,4	+ 2,09
								;
				20			20

Iβ = (10,4 – 1,847; 10,4 + 1,847) = (8,553; 12,247).

1.2.4. Построим доверительный интервал для σx2 (1.10)- (1.12):

ν=19, q = 1 – 0,95=0,05,

		Р1		= 1− 0,05		= 0,975 ; Р2 =			0,05 = 0,025 .
				2					2
Тогда, по табл. 2 приложения найдем: χ12 ≈ 8,83 χ22 ≈ 33,1.
		Следовательно:
		~2		~2		19 15,621 19 15,621
	(n −1)σx			(n −1)σx
			;			=		;		=(8,967;33,613)
	2			2
Iβ =							33,1		8,83
	χ2			χ1

1.3. Задания для выполнения работы Задача: Результаты независимых наблюдений над случай-

ной величиной Х, характеризующей отклонение длины детали от требуемой по техническим условиям, представлены в виде простого статистического ряда. Необходимо построить статистический (вариационный) ряд и гистограмму, найти оценки для математического ожидания и дисперсии, построить соответствующие доверительные интервалы для данного значения β.

Номера вариантов даны в заголовке таблицы заданий.

									Задания (варианты 1-12)																Таблица
№		1		2		3			4			5			6		7		8		9		10	11		12
1		-1,1		1,1		-2,6			3			3			2,5		-2,4		4,8		19,5		0	1		0,7
2		1,5		1,15		-2			1			2,5			2,52		-2,11		5,7		19,72		0,1	1,8		0,5
3		0,8		1,23		-3			1,1			-0,2			2,72		-1,5		4,2		20,1		0,4	3,5		0,517
4		0,1		1,37		-1,3			2,61			2			2,77		-1,23		7		20,21		0,57	1,9		0,52
5		-2		1,4		-2,1			2,4			1			3		-1,01		6		20,44		0,7	0,8		0,66
6		0		1,42		-0,5			1,2			0,7			3,1		-0,13		5		19,8		0,92	2,3		0,641
7		0,2		1,42		-2,2			1,22			0,7			3,34		0,44		4		20,05		1,15	1,8		0,53
8		0,4		1,63		-1			1,3			0,5			3,5		0,58		6,6		20,6		1,17	0		0,56
9		0,3		2,3		-0,9			2,3			1,3			3,52		1,29		6,3		22,3		1,3	1,1		0,565
10		-1		1,5		-1,6			2,21			0,1			2,58		1,78		5,7		22,1		1,6	2,4		0,58
11		-0,1		1,74		1			2,1			0,8			2,6		2		5,5		21,2		3	4,2		0,581
12		1		2,24		-1,7			1,34			0,6			2,61		2,98		6,4		21,35		0,2	2,4		0,61
13		-0,2		1,95		-0,6			1,38			0,2			3,641		3,51		5,9		21,58		0,23	3		0,53
14		-0,1		1,7		-1,8			1,39			1,1			3,94		3,53		5,8		21,62		0,3	1,2		0,51
15		-1,5		1,81		0,1			1,9			2,1			4,4		-1,98		5,5		20,71		0,59	4		0,54
16		0		1,9		0,7			1,84			1,5			2,65		-1,74		6,1		20,89		0,61	2,9		0,535
17		-1,2		1,88		-1,2			1,81			0,2			2,7		-0,84		7,8		21,1		1,05	6		0,55
18		0,2		2,27		-0,8			1,41			1			2,89		0,97		8		21,15		1,1	2,3		0,56
19		2		2,2		-1,5			1,51			-1			2,93		1,12		6,4		21,8		1,2	1,5		0,62
20		0,5		2,12		-1,9			1,6			0,3			3,15		-0,67		6,2		21,92		1,28	2		0,59
21				2,08					1,64						3,17		-0,29				21,17		1,45			0,575
22				2,01					1,7						3,27		2,3				22		1,81			0,571
23									1,75						2,89		2,54						2,3			0,57
									Задания (варианты 13-25)													Продолжение таблицы
№	13		14		15			16			17			18		19		20		21		22	23		24		25
1		2,1	7,5		4,1		1,2			2,52				3		-2,9		6		0,91		0	17,48		1		0,1
2		2,7	7,71		4,6		1,341			2,54				6,3		-3,06		4,1		0,92		0,05	17,34		3,5		0,02
3		2	7,95		4,63		1,35			2,61				7		-5,4		3		1,31		0,7	12,67		-1		0,08
4		1	8,2		4,94		1,4			2,62				6,2		-5,33		5		1,22		0,55	13,5		2		0,04
5		3,7	8,4		5,12		1,5			2,67				4		-5		6,2		1,2		0,3	14,51		2,8		0,13
6		2,2	8,54		4,12		1,62			2,7				4,7		-4,39		2		0,94		0,33	15,49		3		0,2
7		4,6	7,54		4,27		1,9			2,74				5		-4,26		5,1		1		0,29	15,58		2,4		0,28
8		3	7,8		5,17		1,22			2,68				2,2		-4		3,2		0,97		0,17	16,52		0,5		0,37
9		2,1	7,99		5,03		1,27			2,64				5,1		-5,21		5,3		1,1		0,12	16,65		1,7		0,5
10		3,5	8,71		5		1,28			2,63				5,5		-5,17		5,8		1,12		0,11	13,68		1,5		0,09
11		3,2	8,9		4,29		1,7			2,59				4,8		-4,05		4		1,18		0,1	14,31		0		0,1
12		3,4	9,31		4,31		1,6			2,58				5,2		-3,85		4,9		1,27		0,48	14,98		2,6		0
13		4,9	9,48		4,42		1,28			2,57				3,5		-3,44		5,7		1,29		0,43	14,47		2.4		0,11
14		2,8	9,8		4,67		1,31			2,56				4,9		-4,97		4,8		1,13		0,17	15,52		5		0,17

Продолжение табл.

Задания (варианты 13-25)

№	13	14	15	16	17	18	19	20	21	22	23	24	25
15	2,9	9,6	4,54	1,32	2,55	1	-4,65	5	1,05	0,16	16,49	1,9	0,25
16	7	9,35	4,82	1,33	2,57	5,3	-4,33	8	1,01	0,09	16,71	1,1	0,32
17	3	9,28	4,38	1,38	2,8	3,7	-4,15	4,3	1,09	0,07	16,01	2,4	0,39
18	4,8	8,2	4	1,35	2,65	4,7	-3,94	7	1,15	0,13	15,3	4	0,3
19	3,8	8,41	5,21	1,42	2,63	6	-3,17	4,4	1,17	0,37	15,21	2,3	0,22
20	2,9	8,62	5,22	1,58	2,6	4,9	-3,28	5,4	1,35	0,25	14,6	1,9	0,15
21		8,89	3,94	1,36	2,56		-3,37		1,37	0,2	13,15		0,14
22		9,24	3,8	1,47	2,53		-3,67			0,15	13,02		0,12
23			3,72	1,49	2,52					0,14	12,5		0,07

Окончание табл.

Задания (варианты 26-30)

№	26	27	28	29	30
1	3,37	-0,8	0,1	-1,12	1
2	5,3	1,5	0,12	-1,07	5
3	5,68	4	0,17	0,54	2
4	5,97	3	0,22	0,2	3,9
5	6,12	0,5	0,28	0,01	0,2
6	6,74	0,4	0,37	-0,14	2,6
7	6,99	0	0,4	-0,31	3
8	7,28	1	0,6	-0,65	2,5
9	8,21	3,2	0	-0,79	3,8
10	3,52	1,7	0,07	0,37	2,8
11	8,11	1,8	0,08	0,24	-1
12	7,2	-2	0,12	-0,13	2,9
13	6,31	2	0,19	-0,14	4,2
14	7,21	2,5	0,25	-0,92	2,7
15	6,8	0,1	0,31	-0,74	2,4
16	6,28	2,8	0,47	-0,24	3,5
17	5,3	2,6	0,35	-0,05	4
18	4,01	3,5	0,23	0,15	2,9
19	4,24	2,7	0,2	0,19	3,7
20	4,34	1,7	0,18	-0,47	3,4
21	4,73		0,13	-0,85
22	5,26		0,09
23			0,1

Таблица значений β
№ вар.	β		№ вар.	β
1	0,9		23	0,85
2	0,95		24	0,7
3	0,8		25	0,75
4	0,7		26	0,85
5	0,85		27	0,95
6	0,75		28	0,9
7	0,9		29	0,8
8	0,85		30	0,95
9	0,7
10	0,75
11	0,85
12	0,95
13	0,9
14	0,8
15	0,95
16	0,85
17	0,7
18	0,75
19	0,85
20	0,95
21	0,9
22	0,8

2. Указания по выполнению второго задания:

Выравнивание статистических рядов

2.1. Краткие сведения, необходимые для выполнения работы

На практике часто приходится решать вопрос, как при ограниченном объеме выборке подобрать для данного статистического (вариационного) ряда теоретическую кривую функции плотности распределения, в некотором смысле наилучшим образом описывающую статистику.

Вид теоретической кривой определяется из соображений, связанных с существом задачи, а также может быть оценен по построенной гистограмме. Задача сводится к тому, чтобы заменить гистограмму плавной кривой, имеющей достаточно простое аналитическое выражение, и в дальнейшем пользоваться ею

в качестве плотности распределения.
Согласно методу моментов, если f(x) зависит		от двух па-
раметров, то эти параметры выбираются так, чтобы
~	~	(2.1)
mx = mx ;	Dx = Dx .

Для проверки согласованности теоретического и статистического распределений статистический ряд оформляется в виде табл. 2.1.

				Таблица 2.1
X	(x1;x2 )	(x2;x3)	…	(xk;xk+1)
mi	m1	m2	…	mk
Pi*	P1*	P2*	…	Pk*
Pi	P1	P2	…	Pk

где Pi – теоретические вероятности попадания случайной величины в i интервал [xi;xi+1], то есть

xi+1		xi+1	+∞
P1 = ∫	f (x)dx;	Pi = ∫ f (x)dx (i = 2,..., k −1);	Pk = ∫ f (x)dx . (2.2)
−∞		xi	xk

Замечание: Если предполагается, что закон распределения показательный, а xmin ≠ 0 , необходимо «сдвинуть» все исходные зна-

чения случайной величины Х на xmin , т.е. xi =xi −xmin, i =1,...,n и для них строить статистический ряд в виде таблицы, а также использовать в вычислениях.

Для наглядности теоретическое распределение можно оформить в виде графика, совмещая кривую плотности вероятностей и гистограмму. Для этого надо вычислить значения теоретической кривой в граничных точках интервалов разбиения.

В качестве критерия проверки вопроса о согласованности теоретического и статистического распределений чаще всего используется критерий χ2 Пирсона (хи-квадрат). При его использовании берется сумма квадратов отклонений Pi* - Pi статистиче-

ских вероятностей			P*	от гипотетических P	i	, взятых с «весами»:
			i
k	*		2			k		2
χ2 = n∑	(Pi	− Pi )		(2.3) или χ2 = ∑			(mi	−nPi )	. (2.4)
		Pi						nPi
i =1						i =1

Критерий χ2 имеет ν = k − L −1 степеней свободы, где L – количество оцениваемых параметров в законе распределения. (Например, при нормальном законе распределения оценивается дисперсия и математическое ожидание, то есть L = 2). Для распределения χ2 составлены таблицы (табл.2 прилож.). Пользуясь ими, можно для каждого значения χ2 и числа степеней свободы ν найти вероятность р того, что величина, распределенная по закону χ2 , превзойдет это значение. Если эта вероятность достаточна велика, то гипотезу можно признать не противоречащей опытным данным, в противном случае – гипотеза отбрасывается как неправдоподобная.

Можно при проверке воспользоваться следующим: по таблице 2 приложения находится граница χ2кр критической области для заданного уровня значимости критерия q и числа степеней свободы ν . Если χ2 < χ2кр , то можно признать расхождения ме-

жду теоретическим и статистическим распределениями несущественными, то есть выборочный материал не противоречит гипотезе о том, что случайная величина X имеет плотность распределения f(x). В противном случае эта гипотеза не подтверждается.

Подчеркнем, что большое значение вероятности р (например, близкое к единице) не свидетельствует о большом правдоподобии гипотезы.

2.2. Пример выполнения второго задания Для исходных данных из примера 1.2 необходимо подоб-

рать теоретическую функцию распределения (выровнять ряд с доверительной вероятностью β).

2.2.1. Преобразуем выборку в форму статистического (вариационного) ряда. (см. п. 1.2.1)

Гистограмма имеет вид:

Pi *

0,125
0,0125
1	5	9 10,4	13	17	21	x
		Рис. 3

Вычислим m~x и σ~2x (см.

п. 1.2.2);

m~x = 10,4; σ~2x ≈15,621 . Тогда σ~ x = 15,621 ≈ 3,952 .

2.2.2.Учитывая вид гистограммы, выберем в качестве теоретического закона нормальный закон распределения, тогда функция плотности вероятности запишется в виде

			1			− ( x − m x ) 2		(2.5)
f ( x ) =					е		2 σ2x
		σ x	2 π
~	= mx	и	~	= σx , получим теоретическую
Приравнивая mx			σx

кривую в виде (2.5)

	1			−( x −10 , 4 ) 2
f ( x ) =			å	2 15 , 621 .
	3,952	2 π

Построим график этой кривой, для этого вычислим значения f(x) в точке максимума и в граничных точках разбиения на интервалы.

Результаты вычисления сведем в таблицу:

X	1	5	9	10,4	13	17	21
≈ f (x)	0,00597	0,0397	0,0948	0,10095	0,0813	0,025	0,00277

Для упрощения вычислений можно использовать табл. 3 приложения.

Изобразим график на рис. 3. Получим плавную кривую плотности вероятности нормального распределения.