Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

282	r. englman and a. yahalom

313.E. Sjo¨quist, Phys. Lett. A 286, 4 (2001).

314.H. Pothier, P. Lafarge, C. Urbina, D. Esteve, and M. H. Devoret, Europhys. Lett. 17, 1183 (1992).

315.C. Liu, Z. Dutton, C. Behroozi, and L. V. Hau, Nature (London) 409, 490 (2001).

316.D. F. Phillips, A. Fleischhauer, A. Mair, R. L. Walsworth, and M. D. Lukin, Phys. Rev. Lett. 86, 783 (2001).

317.D. DiVicenzo and B. Terhal, Phys. World, March 1998, 53 (1998).

318.D. Bohm, Quantum Theory, Prentice-Hall, New York, 1966, Section 12.6.

319.E. Schro¨dinger, Ann. Phys. 81, 109 (1926). English translation appears in Collected Papers in Wave Mechanics, E. Schro¨dinger, ed., Blackie and Sons, London, 1928, p. 102.

320.W. Gordon, Z. Phys. 41, 117 (1926).

321.W. Greiner, Relativistic Quantum Mechanics: Wave Equations, Springer-Verlag, Berlin, 1997.

322.N. N. Bogoliubov and D. V. Shirkov, Introduction to the Theory of Quantized Fields, Interscience, New York, 1959.

323.W. Gordon, Z. Phys. 50, 630 (1928).

324.P. R. Holland, The Quantum Theory of Motion, Cambridge University Press, Cambridge, UK, 1993.

325.R. L. Seliger and G. B. Whitham, Proc. R. Soc. London Ser. A 305, 1 (1968).

326.E. Madelung, Z. Phys. 40, 322 (1926).

327.I. Talmi, Simple Models of Complex Nuclei, Harcourt, Academic, Chur, 1993.

The Role of Degenerate States in Chemistry: Advances in Chemical Physics, Volume 124.

Edited by Michael Baer and Gert Due Billing. Series Editors I. Prigogine and Stuart A. Rice. Copyright # 2002 John Wiley & Sons, Inc.

ISBNs: 0-471-43817-0 (Hardback); 0-471-43346-2 (Electronic)

QUANTUM REACTION DYNAMICS FOR MULTIPLE ELECTRONIC STATES

ARON KUPPERMANN and RAVINDER ABROL

Arthur Amos Noyes Laboratory of Chemical Physics, Division of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA

CONTENTS

I.Introduction

II. n-Electronic State Adiabatic Representation

A.Born–Huang Expansion

B.Adiabatic Nuclear Motion Schro¨dinger Equation

C.First-Derivative Coupling Matrix

D.Second-Derivative Coupling Matrix III. Adiabatic-to-Diabatic Transformation

A.Electronically Diabatic Representation

B.Diabatic Nuclear Motion Schro¨dinger Equation

C.Diabatization Matrix

D.Application to Two Electronic States

IV. Two-Electronic-State Quantum Reaction Dynamics Formalism for Triatomic Reactions

A.Symmetrized Hyperspherical Coordinates

B.Partial Wave Expansion

C.Propagation Scheme and Asymptotic Analysis V. Summary and Conclusions

Acknowledgment

References

I.INTRODUCTION

Electronic transitions (excitations or deexcitations) can take place during the course of a chemical reaction and have important consequences for its dynamics. The motion of electrons and nuclei were first analyzed in a quantum mechanical framework by Born and Oppenheimer [1], who separated the

283

284	aron kuppermann and ravinder abrol

motion of the light electrons from that of the heavy nuclei and assumed that the nuclei moved on a single adiabatic electronic state or potential energy surface (PES). This Born–Oppenheimer (BO) approximation can break down due to the presence of strong nonadiabatic couplings between degenerate electronic states (due to conical or glancing intersections between those states) or between the near-degenerate ones (due to avoided crossings). These couplings allow for the motion of nuclei on coupled multiple adiabatic electronic states, with the BO approximation replaced by the Born–Huang expansion [2,3] in which an arbitrary number of electronic states can be included.

These nonadiabatic couplings that give rise to electronic transitions can be classified into two categories: (1) Radial couplings, which have been treated by Zener [4], Landau [5], and others [6–11], arise due to translational, vibrational, and angular motions of the atomic or molecular species involved in the chemical process. These couplings allow for transitions to occur between electronic states of the same symmetry. (2) Rotational couplings, which have been studied by Kronig [12] and others [13–19], arise as a result of a transformation of molecular coordinates from a space-fixed (SF) frame to a body-fixed (BF) one due to the conservation of total electron plus nuclear angular momentum. These couplings allow for transitions between electronic states of the same as well as of different symmetries.

An important consequence of the presence of degenerate electronic states is the geometric phase effect. For a polyatomic system involving N atoms, where N 3, any two adjacent adiabatic electronic states can be degenerate for a set of nuclear geometries even if those electronic states have the same symmetry and spin multiplicity [20]. These intersections, occur more frequently in such polyatomic systems than was previously believed. The reason is that these systems possess three or more internal nuclear motion degrees of freedom, and only two independent relations between three electronic Hamiltonian matrix elements (in a simple two electronic state picture) are sufficient for the existence of doubly degenerate electronic energy eigenvalues. As a result, these relations can easily be satisfied explaining thereby the frequent occurrence of intersections. If the lowest order terms in the expansion of these elements in displacements away from the intersection geometry are linear (as is usually the case), these intersections are conical, the most common type of intersection. Assuming the adiabatic electronic wave functions of the two intersecting states to be real and as continuous as possible in nuclear coordinate space, if the polyatomic system is transported around a closed loop in that space (a so-called pseudorotation) that encircles one conical intersection geometry, these electronic wave functions must change sign [20,21]. This change of sign requires the adiabatic nuclear wave functions to undergo a compensatory change of sign, known as the geometric phase (GP) effect [22–26], to keep the

quantum reaction dynamics for multiple electronic states 285

total wave function single valued. This sign change of the nuclear wave function, which is a special case of Berry’s geometric phase [25], is also referred to as the molecular Aharonov–Bohm effect [27] and has important consequences for the structure and dynamics of the polyatomic system being considered, as it greatly affects the nature of the solutions of the corresponding nuclear motion Schro¨dinger equation [26].

The dynamics of chemical reactions on a single ground adiabatic electronic PES has been studied extensively over the last few decades using accurate quantum mechanical time-dependent and time-independent methods. These studies have been successfully applied to triatomic [28–30] and tetraatomic [31,32] reactions in the absence of conical intersections. In the last few years, these studies have been extended to triatomic reactions on a single adiabatic PES including the geometric phase effect [33–37] and to include one or more excited adiabatic electronic PESs [38–42]. These latter studies have been made possible by the availability of ab initio non-adiabatic couplings, the calculation of which has been reviewed previously by Lengsfield and Yarkony [43]. The singular nature of these couplings at the conical intersections of two electronic states, introduces numerical difficulties in the solution of the corresponding coupled adiabatic nuclear motion Schro¨dinger equations. These difficulties are circumvented by transforming the electronically adiabatic representation into a quasidiabatic one [44–55], in which couplings still exist but do not display the singular behavior of the adiabatic representation.

In this chapter, we present a rigorous quantum formalism for studying the dynamics of a polyatomic system (comprising of N atoms) on n electronically adiabatic states, in the absence of spin–orbit interactions. These can be introduced subsequently as perturbative corrections, if they are not too large. In Section II, we present the adiabatic n-electronic-state coupled nuclear motion Schro¨dinger equations and discuss the properties of firstand second-derivative non-adiabatic couplings in this adiabatic representation. Section III deals with the adiabatic-to-diabatic transformation that produces an optimal diabatic representation, in which the nonremovable couplings are minimized. The application of this transformation to the lowest two adiabatic electronic states of H3 [55] is also presented. In Section IV, we introduce the full three-dimensional (3D) quantum reactive scattering formalism for a triatomic system on two adiabatic electronic PESs, capable of providing state-to-state differential and integral cross-sections. This formalism is an extension of the time-independent hyperspherical formalism of Kuppermann and co-workers [33] for a triatomic reaction on a single adiabatic electronic PES, that has been used to perform accurate quantum mechanical reactive scattering calculations (with and without the GP effect included) on the H þ H2 system and its isotopic variants (D þ H2 and H þ D2) [33–37] to obtain differential and integral cross-sections. The cross-sections obtained with the GP effect included were in much better

286	aron kuppermann and ravinder abrol

agreement with the experimental results [56–59] than those obtained with the GP effect excluded. The two-electronic-state reactive scattering formalism and the associated nuclear motion hyperspherical coordinate coupled equations presented in Section IV should provide cross-sections that can be compared with those obtained from a one-electronic-state formalism and yield the energy range of validity of the one-electronic-state BO approximation.

II.n-ELECTRONIC STATE ADIABATIC REPRESENTATION

A.Born–Huang Expansion

Consider a polyatomic system consisting of Nnu nuclei (where Nnu 3) and Nel electrons. In the absence of any external fields, we can rigorously separate the

motion of the center of mass G of the whole system as its potential energy

function V is independent of the position vector of G (r ) in a laboratory-fixed

G

frame with origin O. This separation introduces, besides rG, the Jacobi vectors

R0l ðR0l1 ; R0l2 ; . . . ; R0lNnu 1 Þ and r0 ðr01; r02; . . . ; r0Nel Þ for nuclei and electrons, respectively [26]. These Jacobi vectors are simply related to the position vectors

of those nuclei and electrons in the laboratory-fixed frame. The parameter l refers to an arbitrary clustering scheme for the Nnu nuclei [60,61] and helps specify different product arrangement channels during a chemical reaction.

^
We will omit the kinetic energy operator T		of the center of mass G, since no
G

external fields act on the system and consider only its internal kinetic energy

	^int	given by [26]
	operator T
			^int	^int	^	ð1Þ
	^int	^	T	¼ Tnu	þ Tel
			are, respectively, internal nuclear			and electronic kinetic
	where, Tnu	and Tel

energy operators in the Jacobi vectors mentioned above. If these Jacobi vectors

R0li ði ¼ 1; 2; . . . ; Nnu 1Þ and r0j ðj ¼ 1; 2; . . . ; NelÞ are transformed to their mass-scaled counterparts [61] Rli and rj, the kinetic energy operators have

relatively simple expressions given by

^int

h2

2

^

h2

2

Tnu

¼

2m

rRl

and

Tel

¼

2n

rr

ð2Þ

where

X

X

2

Nnu 1

2

2

Nel

2

ð3Þ

rRl

rRli

and

rr

j¼1

rrj

i¼1

with the Laplacians on the left of these equivalence relations being independent of the choice of the clustering scheme l. The transformation of Jacobi vectors to

quantum reaction dynamics for multiple electronic states 287

the mass-scaled ones is defined by

¼

m

1=2

nj

1=2

Rli

li

Rl0

and

rj ¼

rj0

ð4Þ

m

i

n

where

1

Nnu

1=ðNnu 1Þ

M

1=Nel

m ¼

Y

Mi!

and n ¼ mel

ð5Þ

M

i

1

M þ Nelmel

¼

are the effective reduced masses of the nuclei and electrons, respectively, with Mi being the mass of the ith nucleus. mli and nj in Eq. (4) are the effective masses [26] associated with the corresponding vectors R0li and r0j, with

	nj ¼	½M þ ðj 1Þmel&mel	6	Þ
		M þ jmel
			ð

In Eqs. (5) and (6), M is the total mass of the nuclei and mel is the mass of one electron. By using Eq. (2), the system’s internal kinetic energy operator is given in terms of the mass-scaled Jacobi vectors by

^int		h2				h2
		2			2
T	¼		rRl				rr	ð7Þ
		2m				2n

If V is the total Coulombic potential between all the nuclei and electrons in the system, then, in the absence of any spin-dependent terms, the electronic

^ el

Hamiltonian H is given by

^ el		h2
		2
H	ðr; qlÞ ¼		rr	þ Vðr; qlÞ	ð8Þ
		2n

where, ql is a set of 3ðNnu 2Þ internal nuclear coordinates obtained by removing from the set Rl three Euler angles that orient a nuclear body-fixed frame with respect to the laboratory-fixed (or space-fixed) frame. Due to the small ratio of the electron mass to the total mass of the nuclei, n mel. This approximation is used in the ab initio electronic structure calculations that use the electronic Hamiltonian given in Eq. (8) but with the n replaced by mel. Figure 1 illustrates for a three-nuclei, four-electron system, the corresponding nonmass-scaled Jacobi vectors. The nuclear center of mass G is distinct from

the overall system’s center of mass G. This distinction of the centers of mass and the difference between n and mel is responsible for the so-called mass polarization effect in the electronic spectra of these systems that produces

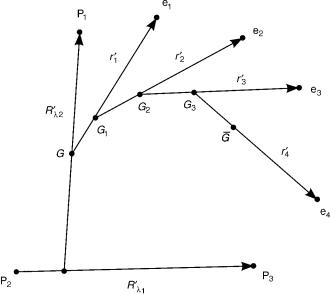
288	aron kuppermann and ravinder abrol

Figure 1. Jacobi vectors for a three-nuclei, four-electron system. The nuclei are P1 , P2 , P3 , and the electrons are e1, e2, e3, e4.

relative shifts in the energy levels of 10 4 or less. In actual scattering calculations, these differences are normally ignored as they introduce relative changes in the cross-sections of the order of 10 4 or less [26].

					functions		el;ad
	The electronically		adiabatic	wave			ci	ðr; qlÞ are	defined as
						^ el
	eigenfunctions of the electronic Hamiltonian H						with electronically adiabatic
	potential energies eiadðqlÞ as their eigenvalues:
	^ el		el;ad		ad		el;ad	ðr; qlÞ	ð9Þ
	H	ðr; qlÞci		ðr; qlÞ ¼ ei		ðqlÞci

The electronic Hamiltonian and the corresponding eigenfunctions and eigenvalues are independent of the orientation of the nuclear body-fixed frame with respect to the space-fixed one, and hence depend only on ql. The index i in Eq. (9) can span both discrete and continuous values. The celi ;adðr; qlÞ form a complete orthonormal basis set and satisfy the orthonormality relations

hciel;adðr; qlÞjciel0 ;adðr; qlÞir						i and i0
¼	>	di i		Þ	for		discrete	ð10Þ
		ð	i0		for	i and i0	continuous
	8 d ;i0
	>	0			for	i discrete and i0 continuous or vice versa
	:
	<

quantum reaction dynamics for multiple electronic states 289

The total orbital wave function for this system is given by an electronically

adiabatic n-state Born–Huang expansion [2,3] in terms of this electronic basis set celi ;adðr; qlÞ as

	X
Oðr; RlÞ ¼	Zi	wiadðRlÞciel;adðr; qlÞ	ð11Þ
P
where, i is a sum over the discrete and an integral over the continuous values

R

of i. The wadi ðRlÞ, which are the coefficients in this expansion, are the adiabatic nuclear motion wave functions. The number of electronic states used in the Born–Huang expansion of Eq. (11) can, in most cases of interest, be restricted to a small number n of discrete states, and Eq. (11) replaced by

Xn

Oðr; RlÞ wiadðRlÞciel;adðr; qlÞ	ð12Þ
i¼1

where n is a small number. This corresponds to restricting the motion of nuclei to only those n electronic states. In particular, if those n states constitute a subHilbert space that interacts very weakly with higher states [62], this would be a very good approximation. The orbital wave function O satisfies the Schro¨dinger equation

^int	ðr; RlÞ	O	ðr; RlÞ ¼ E		O	ðr; RlÞ	ð13Þ
H
where
^ int	ðr; RlÞ ¼		^int	ðr; RlÞ þ Vðr; qlÞ			ð14Þ
H			T

is the internal Hamiltonian of the system that excludes the motion of its center of mass and any spin-dependent terms and E is the corresponding system’s total energy.

B.Adiabatic Nuclear Motion Schro¨dinger Equation

Let us define vadðRlÞ as an n-dimensional nuclear motion column vector, whose components are wad1 ðRlÞ through wadn ðRlÞ. The n-electronic-state nuclear motion Schro¨dinger equation satisfied by vadðRlÞ can be obtained by inserting Eqs. (12) and (14) into Eq. (13) and using Eqs. (7)–(10). The resulting Schro¨dinger equation can be expressed in compact matrix form as [26]

	h2		þ 2Wð1ÞadðRlÞ $Rl þ Wð2ÞadðRlÞg þ feadðqlÞ EIg vadðRlÞ
		fIrR2 l
	2m
¼ 0			ð15Þ

290	aron kuppermann and ravinder abrol

where I, Wð1Þad, Wð2Þad, and ead are n n matrices and $Rl is the column vector gradient operator in the 3ðNnu 1Þ-dimensional space-fixed nuclear configuration space. The parameter I is the identity matrix and eadðqlÞ is the diagonal matrix whose diagonal elements are the n electronically adiabatic PESs eadi ðqlÞ ði ¼ 1; . . . ; nÞ being considered. All matrices appearing in this n-electronic state nuclear motion Schro¨dinger equation (15) are n-dimensional diagonal except for Wð1Þad and Wð2Þad, which are, respectively, the firstand second-derivative [26,43,63–68] nonadiabatic coupling matrices discussed below. These coupling matrices allow the nuclei to sample more than one adiabatic electronic state during a chemical reaction, and hence alter its dynamics in an electronically nonadiabatic fashion. It should be stressed that the effect of the geometric phase on Eqs. (15) must be added by either appropriate boundary conditions [26,33] or the introduction of an appropriate vector potential [23,26,69].

C.First-Derivative Coupling Matrix

The matrix Wð1ÞadðRlÞ in Eq. (15) is an n n adiabatic first-derivative coupling matrix whose elements are defined by

wði;1jÞadðRlÞ ¼ hceli ;adðr; qlÞj$Rl celj ;adðr; qlÞir i; j ¼ 1; . . . ; n ð16Þ

These coupling elements are 3ðNnu 1Þ-dimensional vectors. If the Cartesian components of Rl in 3ðNnu 1Þ space-fixed nuclear congifuration space are

Xl1; Xl2; . . . ; Xl3ðNnu 1Þ, the corresponding Cartesian components of wði;1jÞadðRlÞ are

h	i
wið; jÞ	ðRlÞ l¼ ci	;	ðr; qlÞ		ci	;	ðr; qlÞ r	l ¼ 1; 2; . . . ; 3ðNnu 1Þ
				qXll
1 ad	el ad			q el ad				17
								ð Þ

The matrix Wð1Þad is in general skew-Hermitian due to Eq. (10), and hence its diagonal elements wði;1iÞadðRlÞ are pure imaginary quantities. If we require that the celi ;ad be real, then the matrix Wð1Þad becomes real and skew-symmetric with the diagonal elements equal to zero and the off-diagonal elements satisfying the relation

wið;1jÞadðRlÞ ¼ wjð;1iÞadðRlÞ	i ¼6 j	ð18Þ
As with any vector, the above nonzero coupling vectors ðwið;1jÞadðRlÞ;		i 6¼ jÞ can
be decomposed, due to an extension beyond	three dimensions [26] of the

quantum reaction dynamics for multiple electronic states 291

Helmholtz theorem [70], into a longitudinal part wði;1jÞ;lonad ðRlÞ and a transverse one wði;1jÞ;traad ðRlÞ according to

wið;1jÞadðRlÞ ¼ wið;1jÞ;lonad ðRlÞ þ wið;1jÞ;traad ðRlÞ

ð19Þ

where, by definition, the curl of wði;1jÞ;lonad ðRlÞ and the divergence of wði;1jÞ;traad ðRlÞ vanish

curl wið;1jÞ;lonad ðRlÞ ¼ 0	ð20Þ
$Rl wið;1jÞ;traad ðRlÞ ¼ 0	ð21Þ

The curl in Eq. (20) is the skew-symmetric tensor of rank 2, whose k, l element is given by [26,71]

hcurl wið; jÞ;lon	ðRlÞik;l ¼ qXll		hwið; jÞ;lonðRlÞik	qXlk		hwið; jÞ;lonðRlÞil	ð22Þ
1 ad		q	1 ad		q	1 ad
	k; l ¼ 1; 2; . . . ; 3ðNnu 1Þ
As a result of Eq. (20), a scalar potential ai; jðRlÞ exists for which
	wið;1jÞ;lonad ðRlÞ ¼ $Rl ai; jðRlÞ						ð23Þ

At conical intersection geometries, wði;1jÞ;lonad ðRlÞ is singular because of the ql- dependence of celi ;adðr; qlÞ and celj ;adðr; qlÞ in the vicinity of those geometries

and therefore so is the Wð1ÞadðRlÞ $Rl term in Eq. (15). As a result of Eq. (19),

Wð1Þad can be written as a sum of the corresponding skew-symmetric matrices

Wðlon1Þad and Wðtra1Þad, that is,

Wð1ÞadðRlÞ ¼ Wlonð1ÞadðRlÞ þ Wtrað1ÞadðRlÞ

ð24Þ

This decomposition into a longitudinal and a transverse part, as will be discussed in Section III, plays a crucial role in going to a diabatic representation in which this singularity is completely removed. In addition, the presence of the first derivative gradient term Wð1ÞadðRlÞ $Rl wadðRlÞ in Eq. (15), even for a nonsingular Wð1ÞadðRlÞ (e.g., for avoided intersections), introduces numerical inefficiencies in the solution of that equation.

D. Second-Derivative Coupling Matrix

The matrix Wð2ÞadðRlÞ in Eq. (15) is an n n adiabatic second-derivative coupling matrix whose elements are defined by

wið;2jÞadðRlÞ ¼ hciel;adðr; qlÞjrR2 l cjel;adðr; qlÞir

i; j ¼ 1; . . . ; n

ð25Þ