Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

302 aron kuppermann and ravinder abrol

section as wð1ÞadðRlÞ. For a triatomic system, this vector is six dimensional (6D).

As discussed in Section II.A, the adiabatic electronic wave functions celi ;ad and celj ;ad depend on the nuclear coordinates Rl only through the subset ql (which in the triatomic case consists of a nuclear coordinate hyperradius r and a set of two internal hyperangles nl), this permits one to relate the 6D vector wð1ÞadðRlÞ to another one wð1ÞadðqlÞ that is 3D. For a triatomic system, let aIl ðaIl; bIl; cIlÞ be the Euler angles that rotate the space-fixed Cartesian

frame into the body-fixed principal axis of inertia frame Il, and let $Il be the

Rl

6D gradient vector in this rotated frame. The relation between the space-fixed

$R	and $Il	is given by
l	R
	l
		~	Il	Il	ð60Þ
		$Rl ¼ Rða		Þ $Rl

where RðaIlÞ is a 6 6 block-diagonal matrix whose two diagonal blocks are

both equal to the 3 3 rotational matrix RðaIlÞ. The $Il operator can be

Rl

written as [83]

Il

Il

ðnlÞp

Il

Il

^Il

ða

Il

Þ

ð61Þ

$Rl ¼ G

ðqlÞ þ H

ðnlÞJ

^

In this expression, GIl

and

HIl are

both 6 3

rectangular matrices

whose

elements are known functions of the internal hyperangles nl.

^Il

is a 3 1

p

column vector operator whose elements contain first derivatives with respect to

the three	ql coordinates and	^Il		is the 3		1 column vector operator whose
		J
		^Il		^Il		^Il	of the system’s nuclear motion
elements are the components Jx			, Jy		, and Jz

^

angular momentum operator J in the Il frame. From these properties, it can be

shown that

wð1ÞadðRlÞ ¼ RðaIlÞGIlðnlÞwð1ÞadðqlÞ

ð62Þ

and that

Wð1Þad

ð

R

lÞ $Rl v

ad

ð

R

GIl

ðxlÞ

Wð1Þad

ð

q

l

Il

ad

ð

R

lÞ

ð

63

Þ

lÞ ¼

Þ $Rl v

where

wð1Þad

q

el;ad

ð

r; q

lÞj

p^Il

ð

q

el;ad

ð

r; q

lÞir

ð

64

Þ

ð

lÞ ¼ hc1

lÞc2

is a 3D column vector and Wð1ÞadðqlÞ is a 2 2 skew-symmetric matrix whose only nonzero element is the wð1ÞadðqlÞ vector. By using the symmetrized hyperspherical coordinates defined in Section IV.A for a triatomic system, the

quantum reaction dynamics for multiple electronic states 303

elements of p^Il are the spherical polar components of the 3D gradient associated with the polar coordinates r; y; fl [84]:

0

q

1

qr

p^Il

¼

1

q

ð

65

Þ

B

1r qy q

C

@

A

B

r sin y

qfl

C

The corresponding cartesian gradient $ql is given by

$ql

¼

siny cosfl

cosy cosfl

sinfl

1p^

I

ð66Þ

0 siny sinfl

cosy sinfl

cosfl

l

@

cosy

siny

0

A

in a space whose polar coordinates are r; y; fl.

The wð1ÞadðqlÞ vector can also be decomposed into a longitudinal and a transverse part

wð1ÞadðqlÞ ¼ $ql aðqlÞ þ wtrað1ÞadðqlÞ

ð67Þ

where, aðqlÞ is a scalar potential. It can be shown using Eq. (58) and the two- electronic-state counterpart of Eq. (47) that bðqlÞ ¼ aðqlÞ. The diabatization angle bðqlÞ can be obtained by taking the divergence of Eq. (67) and solving for the resulting Poisson equation

rq2l bðqlÞ ¼ sðqlÞ

ð68Þ

where

sðqlÞ ¼ rql wð1ÞadðqlÞ

ð69Þ

is known because wð1ÞadðqlÞ has been accurately calculated and fitted over the entire ql space of interest [84]. The nuclear–electronic rotational couplings associated with the rotation of the H3 molecular plane relative to a space-fixed frame vanish identically if the mass-scaled nuclear and electronic coordinates of Eqs. (4) and (5) are used and the electronically adiabatic PESs are calculated accordingly. This is not, however, done in standard electronic structure calculations, as mentioned after Eq. (8), and as a result such couplings do not vanish. We have, however, in our electronic wave function calculations [84], found them to be at least two orders of magnitude smaller than the jwð1ÞadðqlÞj.

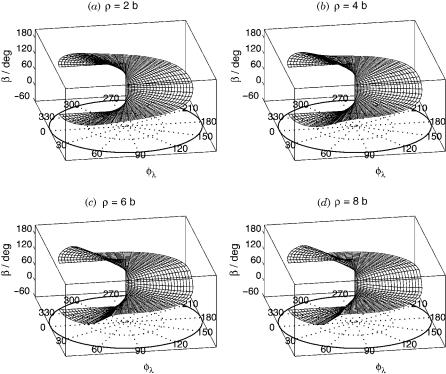
304	aron kuppermann and ravinder abrol

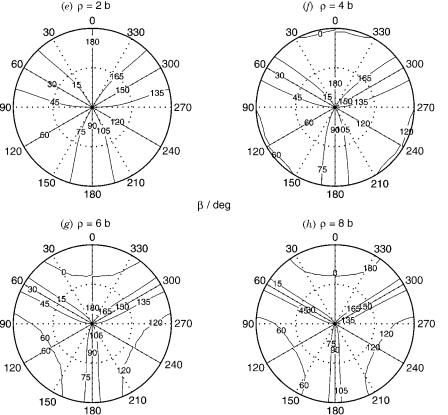
Figure 2. The diabatization angle bðr; y; flÞ, in degrees, for the H3 system at (a) r ¼ 2 b, (b) r ¼ 4 b, (c) r ¼ 6 b, and (d) r ¼ 8 b. The equatorial view of b contours is also given at (e) r ¼ 2 b, (f) r ¼ 4 b, (g) r ¼ 6 b, and (h) r ¼ 8 b.

This justifies the use of the simpler ql language over the Rl one. The solution of the Poisson equation and the boundary conditions used are explained in detail elsewhere [55]. Here, we will present some selected results.

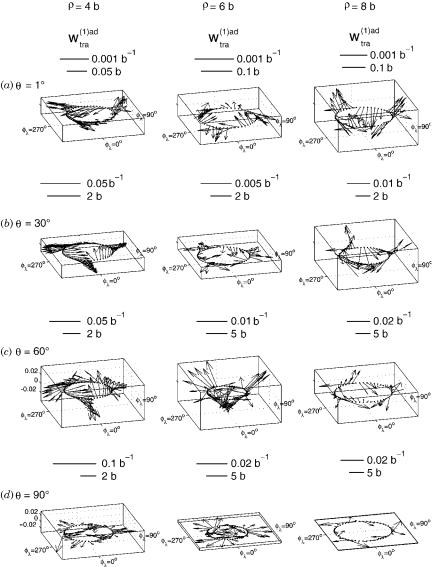
The internal coordinates used in the calculation are the hyperradius r, and the hyperangles y and fl, described in Section IV.A. The equation y ¼ 0 corresponds to conical intersection geometries and y ¼ 90 to collinear ones. For a fixed r and y, as fl is varied from 0 to 2p, the system executes a loop in internal configuration space around the corresponding conical intersection geometry. In Figure 2, the diabatization angle b is displayed for several values of r as a function of y and fl. Use of this b and Eq. (67), furnishes the transverse part wðtra1ÞadðqlÞ over the entire dynamically important region of internal configuration space. This is displayed in Figure 3. These sets of b and wðtra1ÞadðqlÞ were obtained using an optimal mixture of Dirichlet and Neumann

quantum reaction dynamics for multiple electronic states 305

Figure 2 (Continued)

conditions for the solution of the above-mentioned Poisson equation. Using pure Dirichlet conditions instead gives a different transverse part, displayed in Figure 4. Comparison with Figure 3 clearly shows that the optimal boundary conditions significantly reduce the magnitude of the transverse part as compared to all-Dirichlet condition. Comparison of the average magnitude of the transverse vector over the entire internal configuration space for both the optimal and the all-Dirichlet boundary conditions, shows that the optimal condition average was 4.7 times smaller than the all-Dirichlet one. This result indicates that use of the optimal mixed set of Neumann and Dirichlet boundary conditions for solving the Poisson Eq. (68) does indeed significantly reduce the average magnitude of the transverse part of the first-derivative coupling vector.

306	aron kuppermann and ravinder abrol

Figure 3. Transverse (nonremovable) part of the ab initio first-derivative coupling vector, wðtra1Þadðr; y; flÞ as a function of fl for r ¼ 4, 6, and 8 b and (a) y ¼ 1 (near-conical intersection geometries), (b) y ¼ 30 , (c) y ¼ 60 , and (d) y ¼ 90 (collinear geometries).

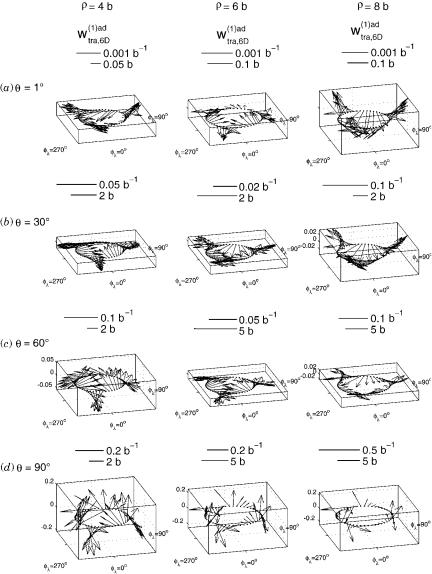
quantum reaction dynamics for multiple electronic states 307

Figure 4. Same as Figure 3 for transverse (nonremovable) part of the ab initio first-derivative coupling vector wðtra1Þ;ad6Dðr; y; flÞ, obtained using the all-Dirichlet boundary conditions.

308	aron kuppermann and ravinder abrol
The vector	wð1Þad q	lÞ	[or	wð1Þad		q	lÞ	] can	also	provide	a good first
	ð			1;2		ð				2 ad	ðqlÞ, which in
approximation to the second-derivative coupling matrix Wð Þ
a two-electronic-state approximation is given by
	Wð2ÞadðqlÞ ¼			w1ð21Þad		q			w1ð22Þad q
				wð2;Þad	ðqlÞ				wð2;Þad	ðqlÞ !	ð70Þ
				2;1	ð lÞ				2;2	ð lÞ

In the two-electronic-state Born–Huang expansion, the full-Hilbert space of adiabatic electronic states is approximated by the lowest two states and furnishes for the corresponding electronic wave functions the approximate closure relation

jc1el;adðr; qlÞihc1el;adðr; qlÞj þ jc2el;adðr; qlÞihc2el;adðr; qlÞj 1

ð71Þ

By using this equation and the fact that for real electronic wave functions the diagonal elements of Wð1ÞadðqlÞ vanish, it can be shown that

wð12;1ÞadðqlÞ ¼ wð22;2ÞadðqlÞ ¼ wð11;2ÞadðqlÞ wð11;2ÞadðqlÞ

wð12;2ÞadðqlÞ ¼ wð22;1ÞadðqlÞ ¼ 0

ð72Þ

For the H3 system, since wð11;2ÞadðqlÞ is known over the entire ql space [84], Eq. (72) can be used to obtain the two equal nonzero diagonal elements of the Wð2ÞadðqlÞ matrix. Since this matrix appears with a multiplicative factor of

ð h2=2mÞ in the adiabatic nuclear motion Schro¨dinger equation giving it the units of energy, both ð h2=2mÞ wð12;1ÞadðqlÞ and ð h2=2mÞ wð22;2ÞadðqlÞ can be labeled as eð2Þad. In Figure 5, this quantity is displayed in units of kilocalories

per mole (kcal/mol) for several values of r as a function of y and fl. It shows the singular behavior of the diagonal elements of Wð2ÞadðqlÞ at conical intersection geometries (y ¼ 0 ). Being a repulsive correction to the adiabatic energies, this singular behavior prevents any hopping of the nuclei from one electronic state to another in the close vicinity of the conical intersection.

By using the diabatic version of the closure relation (71), and Eq. (59), the elements of the diabatic second-derivative coupling matrix Wð2ÞdðqlÞ of Eq. (36) can be expressed as

wð12;1ÞdðqlÞ ¼ wð22;2ÞdðqlÞ ¼ wð11;2Þad;traðqlÞ wð11;2Þad;traðqlÞ

wð12;2ÞdðqlÞ ¼ wð22;1ÞdðqlÞ ¼ 0

ð73Þ

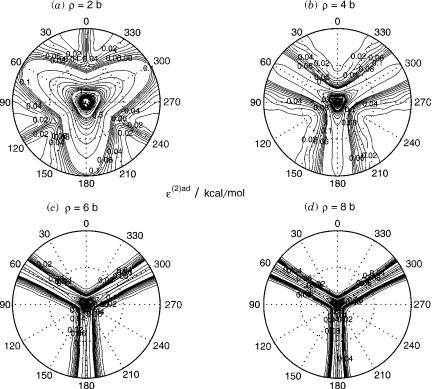
quantum reaction dynamics for multiple electronic states 309

Figure 5. Second-derivative coupling term eð2ÞadðqlÞ defined at the end of Section III.D for the H3 system at (a) r ¼ 2 b, (b) r ¼ 4 b, (c) r ¼ 6 b, and (d) r ¼ 8 b. The following contours are displayed 0–0.1 kcal/mol every 0.01 kcal/mol, 0.1–1.0 kcal/mol every 0.1 kcal/mol and 1.0–10.0 kcal/mol every 0.5 kcal/mol.

where, both ð h2=2mÞ wð12;1ÞdðqlÞ and ð h2=2mÞ wð22;2ÞdðqlÞ can be labeled as eð2ÞdðqlÞ. The values of this (approximate) eð2ÞdðqlÞ calculated from this

equation are smaller than 0.08 kcal/mol over the entire nuclear configuration space involved, and to a very good approximation can be neglected.

IV. TWO-ELECTRONIC-STATE QUANTUM REACTION DYNAMICS

FORMALISM FOR TRIATOMIC REACTIONS

In a two-lowest-electronic-state Born–Huang description for a chemical reaction, the nuclei can move on both of two corresponding PESs during the reaction, due to the electronically non-adiabatic couplings between those states. A reactive scattering formalism for such a reaction involving a triatomic system

310	aron kuppermann and ravinder abrol

is presented below. This formalism is an extension of the time-independent coupled-channel hyperspherical method [26,33–37] that has been used in the past to study triatomic reactions on a single adiabatic electronic state.

A.Symmetrized Hyperspherical Coordinates

Consider a triatomic system with the three nuclei labeled Aa, Ab, and Ag. Let the arrangement channel Al þ AnAk be called the l arrangement channel, where lnk is a cyclic permutation of abg. Let R0l; r0l be the Jacobi vectors associated with this arrangement channel, where r0l is the vector from An to Ak and R0l the vector from the center of mass of AnAk to Al. Let Rl; rl be the corresponding mass-scaled Jacobi coordinates defined by

	Rl ¼	ml;nk		1=2		rl ¼	mnk		1=2
				Rl0	and				rl0	ð74Þ
		m					m

where mnk is the reduced mass of AnAk, ml;nk the reduced mass of the Al; AnAk pair, and m the system’s overall reduced mass given by

m ¼		m mbmg				1=2
		a
	ma	mb	þ	mg
		þ

ml being the mass of atom Al (l ¼ a; b; g). We define a set of symmetrized hyperspherical coordinates r; ol; gl [85,86] by

r ¼ Rl2 þ rl2 1=2	ð75Þ
and
Rl ¼ r cosðol=2Þ rl ¼ r sinðol=2Þ 0 ol p	ð76Þ

where r is independent of the arrangement channel [60,61]. The corresponding internal configuration space Cartesian coordinates are defined by

Xl ¼ r sinol cos gl
Y ¼ r sinol singl	ð77Þ
Zl ¼ r cosol

where gl is the angle between Rl and rl (or R0l and r0l) in the 0 to p range and ol; gl are the polar angles of a point in this space. The alternate internal configuration space symmetrized hyperspherical coordinates y; fl are defined

	quantum reaction dynamics for multiple electronic states 311
as	the polar angles associated with the interchanged
			axes OXl ¼ OZl,
		for which
OYl ¼ OXl, and OZl ¼ OYl
		¼ Zl ¼ r siny cosfl
	Xl
		¼ Xl ¼ r siny sinfl	ð78Þ
	Yl
		¼ Y ¼ r cosy
	Z

The coordinates r, y and fl are limited to the ranges
0 r < 1 0 y p=2	0 fl < 2p	ð79Þ
The relation between y; fl and ol; gl is [using Eqs. (77) and (78)]
siny cosfl ¼ cosol
siny sinfl ¼ sinol cosgl		ð80Þ
cosy ¼ sinol singl

Let GxIlyI zIl be a body-fixed frame Il, whose axes are the principal axes of inertia of the three nuclei and whose Euler angles with respect to the space-fixed frame Gxsf ysf zsf are al; bl; cl with G being the center of mass of the three nuclei. The senses of these axes are chosen to result in a 1:1 correspondence between r; y; fl; al; bl; cl coordinates and the space-fixed Cartesian coordinates of Rl and rl. In addition, the Il axes are labeled so as to order the corresponding principal moments of inertia according to

Izl Ixl Iy

ð81Þ

Furthermore, let l refer collectively to the five hyperangles ðy; fl; al; bl; clÞ, ql to the three internal coordinates ðr; y; flÞ and Rl to all six hyperspherical coordinates.

The coordinates r; l are called the principal axes of inertia symmetrized hyperspherical coordinates. The nuclear kinetic energy operator in these coordinates is given by

h

2

^2

ð lÞ

T^

R

2

T^

82

lÞ ¼

2m rRl ¼

2mr2

ð

Þ

nuð

rðrÞ þ

^

where, TrðrÞ is the hyperradial kinetic energy operator

^

h2 1 q

5

q

TrðrÞ ¼

2m r5 qr r

qr

ð83Þ