Березкин Основы теории информации и кодирования 2010

			1		1	LX	Const	1
	p( yi ) p(xk ) p( yi / xk )			p( yi / xk )		pk			.
	X	X	LX		LX k 1		LX	LY

Симметричный канал – это канал симметричный по входу и выходу.

ТЕОРЕМА 9.3. Пропускная способность дискретного стационарного канала симметричного по входу удовлетворяет неравенст-

LY

ву C log2 LY pi log2 pi , где pi – элементы матрицы

i 1

p( yi / xk ) , i 1, LY . Знак равенства имеет место для симметрич-

ного канала, т.е. максимальная пропускная способность канала реализуется, если распределение событий на выходе равномерное.

ДОКАЗАТЕЛЬСТВО. Представим взаимную энтропию с учетом свойства симметрии:

H ( X ;Y ) H (Y ) H (Y / X );

H (Y / X ) H (Y / xk ) p(xk ) pi log2			L
		pi p(xk ) Y pi log2 pi ;
X	Y	X	i 1
	L
	H (X ;Y ) H (Y ) Y pi	log2 pi .

i 1

Известно, что энтропия ансамбля не превосходит логарифма его мощности H (Y ) log2 LY . Тогда для взаимной энтропии имеем

	L
неравенство	H ( X ;Y ) log2 LY Y pi log2 pi .	Поскольку

i 1

Cmax H (X ;Y ) , то пропускная способность дискретного ста-

{p( xk )}

ционарного канала симметричного по входу также удовлетворяет

L
неравенству C log2 LY Y pi log2 pi . Энтропия	H (Y ) log2 LY
i 1

тогда и только тогда, когда все события на выходе равновероятны,

т.е. p( yi )	1	. Распределение	p(xk ) , при котором p( yi )	1	,
	LY			LY

может в общем случае и не существовать. Если же такое p(xk )

201

существует, то канал обязательно симметричный и

LY

C log2 LY pi log2 pi .

i1

Вкачестве примера рассмотрим дискретный двоичный симметричный канал (ДСК), который задается матрицей условных вероятностей

p( yi / xk )						1 p	p		.
						p	1 p

Матрице соответствует граф переходных вероятностей, приведенный на рис. 9.2. Пропускная способность ДСК вычисляется по

					L
формуле C log2		Y		Y			pi log2 pi 1 p log2	p (1 p) log2 (1 p) .
					i 1
							1 p
(0) x1								(0)	y
									1
					p
					p
(1) x2								(1)	y
							1 p		2

Рис. 9.2. Граф-схема ДСК

Графическая иллюстрация пропускной способности C приведена на рис. 9.3.

1 C

p

1/2 1

Рис. 9.3. График Сдля ДСК

202

9.4. ВЫЧИСЛЕНИЕ ИНФОРМАЦИОННОЙ ПРОПУСКНОЙ СПОСОБНОСТИ СТАЦИОНАРНОГО КАНАЛА

Матрица

условных вероятностей дискретного

канала

p( yi / xk )

по существу представляет собой матрицу

pik

неиз-

менных параметров реального канала. Поэтому взаимную энтропию можно представить в следующем виде:

H ( X ;Y ) f1[ p( xk )] f2 [ p( xk )] ,
							;
где f1[ p( xk )] H (Y )		p( xk ) pik log 2			p( xk ) pik
Y		X			X
f2 [ p( xk )] H (Y / X ) p( xk ) pik log 2 pik .
X	Y

В общем случае, при определении информационной пропускной способности канала, приходится решать следующую экстремаль-

ную задачу с ограничением:								)] ;
C max f		[ p(x		)] f		[ p(x
	{ p( xk )} 1		k		2		k
	p(xk ) 1.
	X

Самый простой способ нахождения условного экстремума состоит в применении метода неопределенных множителей Лагранжа, суть которого состоит в нахождении безусловного экстремума функ-

ционала [ p(xk ), ] f1[ p(xk )] f2[ p(xk )] [1 p(xk )] :

								X
		0						0 , где – неопределенный множитель. Как
				,
	p(xk )
				k	1,LX

правило, данный метод позволяет достичь желаемого результата. Однако следует отметить, что при формулировке экстремальной

задачи совершенно не учитывается условие p(xk ) 0 . Поэтому

при нахождении экстремума можно получить вероятности отрицательные и больше единицы при выполнении в целом условия

p(xk ) 1 . В этом случае поиск экстремума необходимо про-

X

водить на границах области H (X ;Y ) . Встречаются такие случаи крайне редко, и на практике такой подход используется достаточно

203

широко. Тем более, что введение дополнительного ограничения необоснованно усложняет решение задачи в целом.

Найдем пропускную способность для дискретного двоичного симметричного канала со стиранием (ДСКС). ДСКС или канал с контролем задается матрицей условных вероятностей

p(y	/ x )						1 p q	p	q		.
i	k						p	1 p q	q

Матрице соответствует граф переходных вероятностей, приведенный на рис. 9.4.

(0) x1		1 p q		y1 (0)
	p		q

y3 (C )

(1) x2 1 p q

Рис. 9.4. Граф-схема ДСКС

Информационная пропускная способность ДСКС, который является каналом симметричным по входу, вычисляется по более простой схеме:

		LY	pi ;
C max H(Y) pi log2
	p(xk )	i 1
	p(xk ) 1.
		X

Распределение p(x1 ) z , p(x2 ) 1 z , максимизирующее H (Y ) , максимизирует H (X ;Y ) и определяет пропускную способность

канала C . Определим безусловные вероятности

p( y1) z(1 p q) (1 z) p z(1 2 p q) p;

204

p( y2 ) zp (1 z)(1 p q) (1 p q) z(1 2 p q);

p( y3 ) zq (1 z)q q.

Тогда

H (Y ) ln12{[z(1 2 p q) p]ln[z(1 2 p q) p]

[(1 p q) z(1 2 p q)]ln[(1 p q) z(1 2 p q)] q ln q}.

Безусловный экстремум в данном случае будет иметь вид

H (Y )

1

{[(1 2 p q)]ln[z(1 2 p q) p] (1 2 p q)

z

ln 2

(1 2 p q)]ln[(1 p q) z(1 2 p q)] (1 2 p q)} 0.

Откуда находим z 1/ 2 , так как

2z(1 2 p q) 1 2 p q . Наконец,

3

C H(Y)

z 1/ 2

pi log2 pi

i 1

1 q

log2

1 q

3

2

2

2

q log2 q

pi log2 pi

i 1

(1 q)[1 log2 (1 q)] (1 p q)log2 (1 p q) p log2 p.

Поверхность C F[ p, q] приведена на рис. 9.5 [9].

Рис. 9.5. Поверхность Сдля ДСКС

205

9.5. КОДИРОВАНИЕ ПРИ НАЛИЧИИ ШУМОВ

Подведем некоторые итоги. Была введена модель канала передачи информации. Под скоростью передачи информации понимаем среднее количество информации, приходящееся на один канальный символ. Обозначим скорость передачи информации через R H (X ;Y ) H (X ) H (X /Y ) . Очевидно, что R H (X ) , ибо

нельзя принять больше информации, чем посылается.

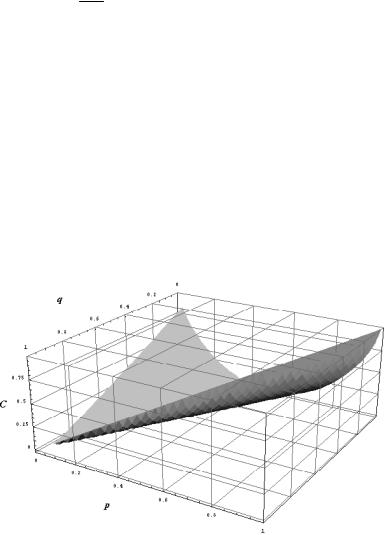
Под пропускной способностью канала C max H ( X ;Y ) по-

{ p( xk )}

нимается максимальное среднее значение информации на символ, которое можно передать по данному каналу. Пропускную способность канала при передаче можно достичь надлежащим выбором источника информации и соответствующим выбором метода кодирования.

Ненадежность передачи по каналу определяется как H (X /Y ) H (X ) R и соответствует неопределенности, которая

имеется на приемном конце по отношению к переданному сообщению после оценки принятого сигнала. Ненадежность удовлетворяет соотношению 0 H ( X / Y ) H (X ) .

ТЕОРЕМА 9.4 (основная теорема Шеннона). Если дискретный источник создает сообщения со скоростью H ( X ) и если

H ( X ) C , то существует такая система кодирования, что сооб-

щения источника могут быть переданы по каналу с произвольно малой ненадежностью. Если H (X ) C , то можно закодировать

сообщения таким образом, что ненадежность передачи по каналу станет меньше, чем H (X ) C где 0 сколь угодно мало, и

не существует способа кодирования, обеспечивающего ненадежность передачи, меньше чем H (X ) C .

Примем теорему без доказательства, но дадим ее более подробную интерпретацию. Итак, теорема утверждает справедливость

неравенств H C H(X /Y) H(X ) C . Существование

вполне определенной пропускной способности для канала с шумом на первый взгляд кажется нереальным. Однако ясно, что можно уменьшить вероятность ошибки, посылая информацию в избыточной форме. Так, например, многократно повторяя передачу сооб-

206

щений и статистически обрабатывая принятые сообщения, вероятность ошибки может быть сделана очень малой. Естественно ожидать, что для того чтобы приблизить вероятность ошибки к нулю, нужно неограниченно увеличивать избыточность кодирования и, следовательно, уменьшать скорость передачи к нулю.

На самом деле это не так. Введенная пропускная способность C имеет вполне определенное значение. Основная теорема для дискретного канала с шумом утверждает, что при надлежащем кодировании по каналу можно передавать информацию со скоростью C со сколь угодно малой частотой ошибок или со сколь угодно малой ненадежностью. Графическая иллюстрация основной теоремы приведена на рис. 9.6. Любая точка заштрихованной области может быть получена при надлежащем выборе способа кодирования, остальные точки, в принципе, получены быть не могут. Наибольший интерес, конечно, представляют точки, лежащие на выделенном горизонтальном отрезке и принадлежащие окрестности выделенной наклонной линии. Именно эти точки соответствуют основной теореме Шеннона.

H ( X / Y )

H C

H (X )

C H

Рис. 9.6. Область допустимых значений ненадежности

Вернемся к рассмотрению уже разобранного примера, когда на вход ДСК поступает равноплотный двоичный код и 1 % символов искажается при передаче.

Информационная								пропускная способность			такого канала
p( y / x )						0,99		0,01		была определена через	H (X ;Y ) . Хотя
i k						0,01	0,99

207

теперь вполне определенно можно записать, что его пропускная

2
способность равна C log2 2 pi log2	pi 0,919 , а ненадеж-
i 1

ность передачи – H (X /Y ) H (X ) C 0,081.

Для того чтобы уменьшить H (X / Y ) до нуля (рис. 9.7), необходимо уменьшить энтропию источника H ( X ) , что неизбежно при-

ведет к неравновероятному использованию двоичных символов и, следовательно, к избыточности. Именно эта избыточность в дальнейшем и должна использоваться для помехоустойчивого кодирования.

H (X )

1	H ( X / Y )

0,919

			0,081
			p	H C
	0,5	1		H(X)
			0,919	1

Рис. 9.7. Иллюстрация основной теоремы Шеннона

Основная теорема Шеннона не дает конкретного метода построения кода, обеспечивающего передачу со скоростью, равной пропускной способности канала. Однако это не уменьшает фундаментального значения теоремы, которая в области помехоустойчивого кодирования стимулирует поиск новых оптимальных корректирующих кодов и дает оценку их эффективности.

ЗАДАЧИ

9.1. Вывести формулы оценки информационной пропускной способности дискретного двоичного канала (ДК) (рис. 9.8) без па-

мяти. Построить поверхность C F[ p1 , p2 ] .

208

9.2. Определить информационную пропускную способность канала, состоящего из двух последовательно соединенных двоичных симметричных каналов (ДСК).

(0)	x1			1 p1			y1	(0)
		p1				p2
(1)	x						y2	(1)
				1 p2
	2

Рис. 9.8. Граф-схема ДК

9.3.Сообщения равноплотным двоичным кодом передаются на вход канала. В процессе передачи из-за искажений 1 % символов принимается неправильно. Вычислить информационную пропускную способность двоичного симметричного стационарного канала.

9.4.Два одинаковых двоичных симметричных канала соединены параллельно, т.е. один и тот же символ передается по обоим каналам. Какова информационная пропускная способность такой системы, если информация стирается, когда на выходе символы не совпадают?

9.5. Два одинаковых двоичных симметричных канала соединены параллельно, т.е. один и тот же символ передается по обоим каналам. Какова информационная пропускная способность такой системы, если в случае искажений ошибка по обоим каналам не обнаруживается?

9.6. Определить информационную пропускную способность канала, заданного матрицей условных вероятностей

p( yi / xk )

1

1 p

1 p

p

p

.

2

p

p

1 p

1 p

9.7. Определить информационную пропускную способность канала, заданного матрицей условных вероятностей

209

					1 p	p	0	0
p( yi / xk )					p	1 p	0	0		.
					0	0	1 p	p
					0	0	p	1 p

9.8. Определить информационную пропускную способность канала, заданного матрицей условных вероятностей

					1 p	p	0		.
p( yi / xk )					p	1 p 0
					0	0	1

210