Березкин Основы теории информации и кодирования 2010

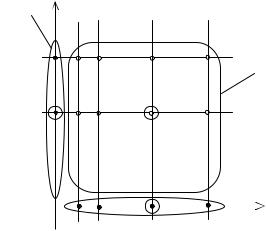
p(xk yi ) p(xk ) ;				p(xk yi ) p( yi ) ;
yi Y				xk X
p(xk / yi )	p(xk yi )		;	p( yi / xk )	p(xk yi )	.
	p( yi )
					p(xk )

Все приведенные соотношения удобно интерпретировать графически (рис. 6.2).

Y
ym	(xk , yi )	XY
p( yi ) yi	p(xk yi )

y2

y1 X

x1 x2 ... xk ... xn p(xk )

Рис. 6.2. Графическая иллюстрация декартового произведения

Произведение множеств XY образовано совокупностью точек (xk , yi ) . Каждый столбец этой совокупности соответствует точке

xk X , а каждая строка – точке yi Y . Другими словами, точки

множеств X и Y могут рассматриваться как координаты точек

(xk , yi ) XY .

Вероятность p(xk ) есть сумма вероятностей p(xk yi ) по всем

точкам столбца с		xk . Аналогично, p( yi ) есть сумма вероятностей
p(xk yi )	по всем элементам строки с yi . Условная вероятность
p(xk / yi )	равна	вероятности, предписанной точке (xk , yi ) –

141

p(xk yi ) , деленной на сумму по строке yi , а условная вероятность p( yi / xk ) равна p(xk yi ) , деленной на сумму по столбцу xk .

Подобным образом можно определить произведение большего числа множеств и ввести соответствующие распределения.

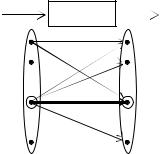
Введем способ измерения информации, содержащейся в yi относительно xk . Будем трактовать xk и yi как случайные собы-

тия или сообщения на входе и выходе некоторой системы. В этом нет ничего принципиально нового, с таким подходом мы встречаемся в кибернетике достаточно часто (рис. 6.3).

xk X	Система	yi Y
	x1	y1
	x2	y2
	...	...
	xk	yi
	...	...
	xn	ym

Рис. 6.3. Передача информации через систему

Встанем на позиции внешнего наблюдателя, который следит за системой со стороны и которому известны события и на входе, и на выходе. С позиции этого наблюдателя определим, в какой сте-

пени yi определяет xk . Другими словами, определим меру количества информации, переданной через систему, или какую информацию в количественном смысле содержит yi относительно xk .

Предполагается, что вход системы в некотором смысле определяет ее выход. Это требование вполне естественно, иначе о какойлибо передаче сообщений не могло быть и речи.

Пусть некоторый источник информации может порождать семь различных равновероятных сообщений, которые кодируются двоичным кодом и посимвольно передаются адресату (табл. 6.1).

Предположим, что передается сообщение с номером 2. Априорная вероятность получить это сообщение равна 1/7. После того как

142

принят первый символ "0", из рассмотрения исключаются коды с номерами 4, 5, 6, 7, начинающиеся с символа "1", и вероятность получения кода 2 возрастает. Расчет этой вероятности прост и сво-

дится к простой нормировке p(u		/ y0 )			1/	7		1/ 3 . По-
	2	1	1/ 7		1/	7	1/ 7

сле принятия второго символа "1" вероятность получения кода 2 равна 1/2 , а после принятия последнего символа "0" неопределенность полностью исчезает. В этом случае вероятность приема сообщения с номером 2 при последовательной посимвольной передаче изменяется от 1/7 до 1.

Сообщение

uk

u1 u2 u3 u4 u5 u6 u7

Вероятность сообщения

p(uk )

1/7

1/7

1/7

1/7

1/7

1/7

1/7

Таблица 6.1

	Двоич-				Вероятность появления на выходе k - го
					сообщения при условии появления одного,
	ный
						двух и трех символов
	код
					p(uk / y10 )	p(uk / y10 y12 )	p(uk / y10 y12 y30 )
	y y	2	y	3
	1
	001				1/3	0	0
	010				1/3	1/2	1
	011				1/3	1/2	0
	100				0	0	0
	101				0	0	0
	110				0	0	0
	111				0	0	0

Разобранный пример показывает, что информация, содержащаяся в yi (010) относительно xk (u2 ) , сводится к изменению ве-

роятности от априорного значения p(xk ) p(u2 ) 1/ 7 к апосте-

риорному p(xk / yi ) p(u2 / y10 y12 y30 ) 1.

Удобной мерой этого изменения оказался логарифм отношения

апостериорной вероятности p(xk / yi ) к априорной		p(xk ) . Коли-
чество информации, содержащееся в событии	yi	относительно
события xk , определяется как J (xk ; yi ) loga	p(xk / yi )		и носит
	p(xk )

название взаимной информации.

143

Основание логарифма определяет единицу измерения количества информации. Если берется двоичный логарифм, то информация измеряется в битах, если натуральный логарифм, то в натах, если десятичный логарифм, то в дитах (хартли). Количественно эти меры соотносятся следующим образом:

1 нат = 1,44 бит;

1 дит = 2,30 нат = 3,32 бит.

На практике чаще применяют двоичный логарифм, так как он непосредственно дает количество информации в битах, что хорошо согласуется с двоичной логикой вычислительных машин. В теоретических расчетах удобнее пользоваться натуральным логарифмом из-за простоты операций дифференцирования и интегрирования.

Наконец, выбранная логарифмическая мера количества информации удобна по следующим причинам:

1. Многие технические параметры зависят линейно от логарифма числа возможностей. Например, добавление одного разряда к регистру удваивает число возможных состояний регистра. Тем самым прибавляется единица к логарифму этого числа при осно-

вании два n 1 log2 2n 1.

2.Логарифмическая мера ближе к нашему интуитивному представлению о подходящей мере. Мы измеряем количества с помощью линейного сравнения с принятыми эталонами. Естественно для нас считать, что два одинаковых запоминающих устройства должны обладать вдвое большей памятью для хранения информации, чем одно; а два идентичных канала должны иметь удвоенную пропускную способность.

3.С математической точки зрения логарифмическая мера более проста, так как многие операции, в частности операции предельного перехода, осуществляются наиболее просто при использовании логарифмов.

6.2.ОСНОВНЫЕ СВОЙСТВА ВЗАИМНОЙ ИНФОРМАЦИИ

1.Взаимная информация обладает свойством симметричности:

	J (x	; y ) log		p(xk /	yi ) p( yi )	log		p(xk yi )
			2 p(x		) p( y )		2 p(x ) p( y )
	k	i
				k	i			k	i

144

p(xk yi ) p(xk ) p( yi )

log	2	p(xk ) p( yi / xk )	log	2	p( yi / xk )	J ( y ; x ) .
		p(xk ) p( yi )			p( yi )		i	k
Другими словами, информация, содержащаяся в							yi	относительно

xk , равна информации, содержащейся в xk относительно yi . Поэтому J (xk ; yi ) называют взаимной информацией между событиями xk и yi . Взаимная информация является мерой статистической связи двух событий, сообщений. Действительно, если события независимы, то и J (xk ; yi ) 0 .

2. Взаимная информация положительна J (xk ; yi ) 0 , если ус-

ловная вероятность появления одного события при условии, что второе событие уже произошло, больше безусловной вероятности

его появления – p(xk / yi ) p(xk ) . Взаимная информация отрицательна J (xk ; yi ) 0 , если условная вероятность осуществления события меньше безусловной вероятности – p(xk / yi ) p(xk ) .

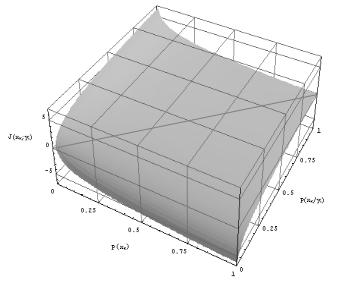
Характер зависимости взаимной информации от апостериорной и априорной вероятностей приведен на рис. 6.4.

Рис. 6.4. Взаимная информация

145

Для определения других свойств взаимной информации положим, что (xk , yi , z j ) – упорядоченная тройка множества XYZ , и

введем в рассмотрение модель, в которой будем считать, что xk – событие на входе системы, а yi , z j – символы, порождаемые на

выходе этой системы.

3. Условная взаимная информация определяется следующим

образом: J (x ; z		/ y ) log		p(xk	/ yi z j )		.
			2 p(x
k	j	i			k	/ y )
						i

4. Свойство аддитивности. Пусть J (xk ; yi z j ) – взаимная ин-

формация события xk и пары ( yi , z j ) . Выразим взаимную информацию J (xk ; yi z j ) через информацию, которую несет символ yi относительно события xk , и информацию, которую несет символ

z j относительно того же события xk

:

J (x

; y z

) log

p(xk / yi z j ) p(xk

/ yi )

log

p(x /

y )

j

2

2

k

i

k

i

p(xk ) p(xk / yi )

p(xk )

log

p(xk / yi z j )

J (x

; y

) J (x

; z

/ y

) .

(6.1)

2 p(xk / yi )

k

i

k

j

i

Информация, содержащаяся в символах

yi и z j

, равна сумме ин-

формации, содержащейся в символе

yi

относительно

xk , и ин-

формации,

содержащейся в символе

z j , при условии,

что yi из-

вестно.

Порядок символов в (6.1) безразличен, поэтому

J (xk ; yi z j ) J (xk ; yi ) J (xk ; z j / yi ) J (xk ; z j ) J (xk ; yi / z j ) .

Суммируя оба выражения, получаем

J (xk ; yi z j ) 1

[J (xk ; yi ) J (xk ; z j ) J (xk ; yi / z j ) J (xk ; z j / yi )].

2

В силу свойства симметричности можно рассматривать J ( yi z j ; xk ) как количество информации, которое содержится в xk относи-

тельно пары ( yi , z j ) : J ( yi z j ; xk ) J ( yi ; xk ) J (z j ; xk / yi ) .

146

Рассмотрим пример. Пусть на вход кодера может поступать семь сообщений, которые он кодирует в трехразрядный двоичный код (табл. 6.2). На выходе кодера порождается последовательность в виде трех символов. Используя свойство аддитивности информации, вычислим, какое количество информации несет кодовая по-

следовательность 010 относительно сообщения u2 , и какое коли-

чество информации несет каждый двоичный символ об этом сообщении.

Сообщение

uk

u1 u2 u3 u4 u5 u6 u7

Вероятность сообщения

p(uk )

1/2

1/8

1/8

1/16

1/16

1/16

1/16

						Таблица 6.2
Двоич-				Вероятность появления на выходе k -го со-
				общения, при условии появления одного, двух
ный					и трех символов
код
				p(uk / y10 )	p(uk / y10 y12 )	p(uk / y10 y12 y30 )
y y	2	y	3
1
001				2/3	0	0
010				1/6	1/2	1
011				1/6	1/2	0
100				0	0	0
101				0	0	0
110				0	0	0
111				0	0	0

Если кодер работает идеально, без ошибок, то сообщение u2

несет относительно кодовой последовательности или кодовая последовательность относительно сообщения следующее количество информации:

J (u		; y0 y1 y0 ) log		p(u	2	/ y0 y1 y0 )	log		1	3 .
						1 2 3
						p(u2 )			p(u2 )
	2	1 2 3	2					2

Посимвольный вклад, т.е. количество информации, которое несет каждый последующий символ о сообщении u2 , имеет вид

J (u		; y0 ) log			P(u		2	/ y	0 )		log				1/ 6	log			4 / 3;
								1
															1/ 8
	2	1		2	P(u2 )								2					2
J (u		; y1	/ y0 ) log				P(u		2	/ y0 y1 )					log		1/ 2		log		3;
											1	2
						2 P(u					/ y0 )						2 1/ 6
	2	2	1							2										2
												1

147

J (u		; y0	/ y0 y1 ) log		P(u	2	/ y0 y1 y0 )				log		1		log		2.
								1	2	3
				2 P(u				/ y0 y1 )					1/ 2
	2	3	1 2				2					2				2
									1	2

Используя свойство аддитивности, получаем

J (u2 ; y10 y12 y30 ) J (u2 ; y10 ) J (u2 ; y12 / y10 ) J (u2 ; y30 / y10 y12 ) 3 .

6.3. СОБСТВЕННАЯ ИНФОРМАЦИЯ

Введем теперь в рассмотрение понятие собственной информа-

ции. Очевидно, что p(xk / yi ) 1 . Следовательно,
J (x	; y ) log		p(xk / yi )		log		1	log		p(x ) J (x ) .
		2 p(x )				2 p(x )
k	i								2	k	k
			k				k
Назовем J (xk ) log2 p(xk )					количеством собственной информа-

ции xk .

Таким образом, информация какого-либо события измеряется логарифмом величины, обратной величине вероятности появления этого события (рис. 6.5). Отсюда следует, что чем меньше вероятность появления события, тем больше информации оно в себе содержит.

J (xk ) log2 p(xk )

	1			p(xk )
		log2	p(xk )

Рис. 6.5. Собственная информация

Если вернуться к примеру кодера с безошибочным кодированием, сообщение на его входе xk требует для своего однозначного

определения количества информации J (xk ) log2 p(xk ) . Взаимная информация между xk и yi становится равной собственной информации, т.е. J (xk ) J (xk ; yi ) , когда p(xk / yi ) 1. Тогда yi

148

однозначно определяет xk , а J (xk ) log2 p(xk ) можно трактовать как максимальное количество информации, которое нужно иметь о сообщении xk .

Используя понятие собственной информации, можно несколько иначе интерпретировать взаимную информацию:

J (x

k

; y ) log

2

p(xk / yi )

log

2

p(x

k

) log

2

p(x

k

/ y )

i

p(xk )

i

J (xk ) J (xk / yi ) ,

где J (xk / yi ) log2 p(xk / yi ) . Информация, содержащаяся в событии yi относительно xk , равна разности между количествами информации, требуемой для идентификации xk до и после того, как становится известным событие yi .

Симметричное представление взаимной информации приводит

	к формулам:			p(xk yi )
	J (x	; y ) log				J (x ) J ( y ) J (x y );
			2 p(x ) p( y )
	k	i				k	i	k i
				k	i
	J (xk yi ) log2 p(xk yi )				J (xk ) J ( yi ) J (xk ; yi ).

6.4. МЕРА ИНФОРМАЦИИ КАК СЛУЧАЙНАЯ ВЕЛИЧИНА

Как можно видеть из предыдущих подразделов, введенные меры количества информации являются случайными величинами, т.е. числовыми функциями элементов выборочного пространства.

Мера информации является довольно необычной случайной величиной, так как ее значение зависит от вероятностной меры, однако с ней можно обращаться так же, как с любой случайной величиной.

Например, собственная информация является случайной величиной, так как зависит от распределения вероятностей событий.

Мера информации J (xk ), xk X принимает на множестве X различные значения log2 p(xk ) с вероятностью p(xk ) и имеет распределение p{J (xk ) J}.

149

Аналогичным образом определяется и взаимная информация как случайная величина J (xk ; yi ), (xk , yi ) XY , которая на множе-

	стве XY принимает различные значения log2	p(xk / yi )	с вероят-
		p(xk )

ностью p(xk yi ) и имеет распределение p{J (xk ; yi ) J}.

Собственная и взаимная информации имеют среднее значение, дисперсию и моменты всех порядков:

m[J (xk )] J (xk )p(xk ) J (X );

xk X

D[J (xk )] [J (xk ) J ( X )]2 p(xk );

xk X

m[J (xk ; yi )]	J (xk ; yi )p(xk yi ) J (X ;Y );
	( xk , yi ) XY
D[J (xk ; yi )]	[J (xk ; yi ) J ( X ;Y )]2 p(xk yi );
	( xk , yi ) XY

...

В качестве примера рассмотрим источник информации со статистикой, представленной в табл. 6.3.

						Таблица 6.3
		Вероятность		Собствен-	Распределение
Сообщение		сообщения		ная инфор-	вероятностей
uk		p(uk )		мация	p{J (uk ) J}
				J (uk )
u1		1/2		1	p{J (uk ) 1} 1/ 2
u2		1/8		3
u3		1/8		3	p{J (uk ) 3} 1/ 4
u4		1/16		4
u5		1/16		4	p{J (uk ) 4} 1/ 4
u6		1/16		4
u7		1/16		4
Распределение		количества		собственной		информации

p{J (uk ) J} представлено на рис. 6.6. Функция распределения F(J ) p{J (uk ) J} (рис. 6.7) определяется обычным образом с

150