Загребаев Методы матпрограммирования 2007

2.1.2.Сведение матричной игры

кзадаче линейного программирования

Как правило, любая матричная игра может быть сведена к паре двойственных задач линейного программирования. Чтобы преобразование было корректным, необходимо выполнение условия v > 0. Это условие обязательно выполняется, если все элементы платежной матрицы неотрицательны. Добиться неотрицательности можно путем прибавления достаточно большой константы ко всем элементам матрицы, что не меняет множества оптимальных стратегий игроков, так как приводит к игре стратегически эквивалентной ис-

ходной [28], [29].

В теории игр доказывается следующая теорема.

Теорема 2.1. Пусть множество V ′ состоит из тех и только тех чисел v′ , для которых существует такая стратегия Y игрока 2, что справедливы неравенства

′	(2.6)
H (i, Y ) ≤ v , i =1, m,

тогда значение цены матричной игры v равно наименьшему из чисел

множества V ′, а вектор Y * , для которого эти неравенства справедливы при v′ = v , является оптимальной стратегией игрока 2.

Таким образом, чтобы найти v и Y * , надо определить минимальное значение v′ , удовлетворяющее неравенствам (2.6), которые удобнее записать так:

n
∑aij y j		′	i =1, m .						(2.7)
	≤ v ,
j=1
Разделим обе части неравенства						(2.7) на v′			и положим
u j = y j / v′, тогда оно примет вид
n
∑aij u j ≤1,			i =	1, m			.		(2.8)
j=1
С учетом того, что
n	1 n					1
∑u j =		∑ y j =					,		(2.9)
						v′
j=1	v′ j=1

111

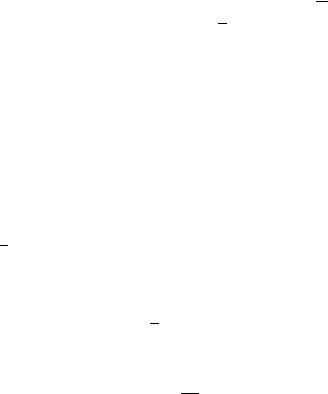
задача минимизации v′ сводится к задаче максимизации v1′ или,

что то же самое, максимизации функции f (u ) , т.е. получили зада-

чу линейного программирования, которую можно сформулировать в виде:

найти

					n
										(2.10)
max f (u )= ∑u j
					j=1
при ограничениях:
n
	∑aiju j ≤1, i =1, m;
j=1
	u		≥ 0,M j =
		j				1, n.

Пусть u * = (u1* , ..., un* )– оптимальное решение полученной зада-

чи линейного программирования, тогда искомая цена игры определяется соотношением:

v =	1			.	(2.11)
	f (	u	* )

Исходя из этого, компоненты оптимальной стратегии второго

игрока можно представить в виде
y*j = vu*j , j =1, n .	(2.12)

Необходимость упомянутого ранее условия неотрицательности ( ν > 0 ) для корректности проведенных преобразований очевидна.

Приведенную выше теорему 2.1 можно аналогичным образом применить и к стратегиям первого игрока. Из неё следует, что для

определения цены игры ν и оптимальной стратегии X * необходимо найти максимальное значение числа ν′′ , удовлетворяющее неравенствам:

m	′′
∑aij xi ≥ ν , j =1, n.
i=1

112

В результате, полагая t i = xi 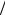ν′′ , приходим к следующей задаче

линейного программирования: найти

				m						(2.13)
min ϕ(t )= ∑ti
				i=1
при ограничениях:
m
					j =1, n;
∑aij ti ≥1,
i=1
	ti ≥ 0, i			=1, m.

Тогда, если t * = (t1* , ..., tm* ) – оптимальное решение этой задачи,

то цена игры определяется соотношением аналогичным выраже-

нию (2.11):

v =	1	,	(2.14)
	ϕ(t * )

и, соответственно, компоненты оптимальной стратегии первого игрока задаются в виде

xi* = vti* , i =		.	(2.15)
	1, m

Как видно, вторая задача (2.13) является двойственной к первой (2.10), поэтому справедливо равенство:

f (

u

* )= ϕ(t

* ).

(2.16)

Как отмечено в разд. 1.5 данной книги, решение двойственных задач линейного программирования осуществляется одновременно, путем однократного применения симплекс-метода.

Таким образом, сведение любой матричной игры к задаче линейного программирования приводит к необходимости, с одной стороны, максимизации функции f (u ):

		n
max f (u )= ∑u j
		j=1

113

при ограничениях:

n
	∑aiju j ≤1 i =1, m;
j=1
	u		≥ 0, j =
		j		1, n,

где u j = y j 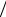ν′.

С другой стороны, минимизации функции ϕ(t ):

						m
		min ϕ(t )				= ∑ti
	при ограничениях:					i=1
	m
			≥1,			j =1, n;
	∑aij ti
	i=1
		ti ≥ 0, i =1, m,

где ti = xi 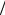v′′.

Легко видеть, что вторая задача является двойственной к первой, более того, и первая и вторая задача прекрасно сводятся к канонической форме записи задачи линейного программирования, которая успешно решается методами, изложенными в гл. 1 настоящего издания.

2.2. Оптимальное распределение запасов реактивности при работе системы ядерных реакторов

впеременном суточном графике нагрузки

2.2.1.Физическая постановка задачи

Вусловиях широкого ввода ядерно-энергетических мощностей и растущего разуплотнения графиков нагрузок энергосистем, использование атомных электростанций (АЭС) в базовой части графика нагрузок будет представлять все большие трудности. Поэтому часть электростанций вынуждена будет работать в соответствии с суточными и сезонными колебаниями потребности в электроэнергии.

При этом, решение проблемы маневренности энергоблоков АЭС возможно только после проведения комплекса научно-исследова-

114

тельских и опытно-конструкторских работ. Основные из них следующие:

1)снятие ограничений на число циклов пуск-остановка для всего оборудования АЭС;

2)улучшение схем пусков и остановок АЭС и снижение потерь тепла при расхолаживании блоков за счет рационального использования остаточного энерговыделения ядерного топлива и теплоаккумулирующей способности графитовой кладки;

3)решение проблемы выбора оптимального типа топлива, защитных оболочек для него и конструкций тепловыделяющих элементов с учетом работы реакторов при переменных нагрузках;

4)приведение в соответствие с требованиями эксплуатации систем управления и защиты реакторов и обеспечение реакторов необходимым запасом реактивности.

Первые три проблемы носят, в основном, теплотехнический и прочностной характер, в то время как последняя связана с физикой ядерного реактора и обусловлена нестационарным отравлением реактора ксеноном.

Обеспечение реактора оперативным запасом реактивности, позволяющим компенсировать нестационарное отравление ксеноном, приводит к снижению энерговыработки реактора. Потерю энерговыработки реактора, работающего в переменном графике нагрузки, по сравнению с энерговыработкой при работе на номинальной мощности, можно связать с резервируемым запасом реактивности соотношением

∆Q =	∆ρ	,	(2.17)
	a
где a – темп выгорания, 1/(кВт сут); ∆ρ			– запас реактивности,

отн. ед.; ∆Q = Qm −Q – разность между энерговыработкой при работе в базисном режиме ( Qm ) и режиме переменных нагрузок ( Q ),

кВт сут.

Величина резервируемого запаса реактивности, а следовательно, и потеря энерговыработки реактора, зависит от требуемой длительности работы реактора на пониженной мощности W, от степени

снижения мощности реактора ε = W , где Wн – номинальная мощ-

Wн

115

ность реактора, от величины плотности потока нейтронов при работе на номинальной мощности и других характеристик реактора.

В рамках точечной модели запас реактивности, обеспечивающий работу реактора на пониженной мощности εWн в течение произвольного времени после снижения мощности равен

∆ρ = xм − xр ,

(2.18)

где xм и xр – максимальная и равновесная концентрации ксенона,

	нормированные на	ν f Σ f	;	Σ f	– макроскопическое сечение деле-
		σX

ния активной зоны реактора; ν f – среднее число вторичных ней-

тронов на акт деления; σX – сечение поглощения ксенона, см2.

На АЭС, как правило, устанавливается несколько энергоблоков. В общем случае энергоблоки могут отличаться электрической мощностью, темпом выгорания, другими характеристиками и работать независимо друг от друга. Условием, связывающим реакторы, входящие в состав АЭС, является выработка заданного количества электроэнергии атомной электростанцией.

При ограниченном оперативном запасе реактивности, например, для реакторов с непрерывной перегрузкой или в конце кампании для реакторов с дискретной перегрузкой возникает задача оптимизации распределения запасов реактивности в системе реакторов с целью минимизации суммарной потери энерговыработки при удовлетворении заданному графику суточного снижения мощности.

Математически задача формулируется следующим образом: найти

min

∆ρ1 ... ∆ρN

при ограничениях:

N ∆ρ∑ ii=1 ai

N
∑	δi εi (∆ρi ) = α;
i=1	(2.19)

0 ≤ ∆ρi ≤ ∆ρi m , i =1, ..., N,

116

	где	N – число реакторов на станции; ∆ ρ i – оперативный запас
	реактивности i-го реактора;						εi – степень снижения мощности i-го
	реактора;		α		–	заданная	степень снижения мощности АЭС,
		N
		∑Wi
	α =	i=1	;	δ	i	– доля электрической мощности i-го реактора,
		N
		∑Wi н

i=1

δi = NWi н .

∑Wi н

i=1

Заметим, что оптимизация возможна только при < 0 < α <1 , так как при α = 0 и α =1 значения оперативных запасов реактивности

определены:

∆ρi = ∆ρi м, ∆ρi = 0.

Поэтому качественно понятно, что эффект от оптимизации будет сильнее всего сказываться в средней части диапазона изменения α . Вид зависимости ε(∆ρ) возможной степени снижения

мощности реактора от запаса реактивности, вообще говоря, определяется режимом изменения мощности реактора.

Наиболее простым режимом для анализа является снижение мощности реактора с максимально возможной скоростью до определенного уровня и поддержание реактора на данном уровне до момента выхода АЭС на номинальную мощность. Характер зависимости ε(∆ρ) при различных плотностях потоков нейтронов этом

случае показан на рис. 2.1.

Как видно из рисунка, при малых плотностях потока нейтронов зависимость ε(∆ρ) представляет собой практически линейную

функцию. С увеличением плотности потока нейтронов нелинейность в характере зависимости ε(∆ρ) увеличивается.

В данном разделе рассмотрено решение задачи для системы реакторов с линейной зависимостью возможной степени снижения мощности от запаса реактивности. (Решение задачи для системы

117

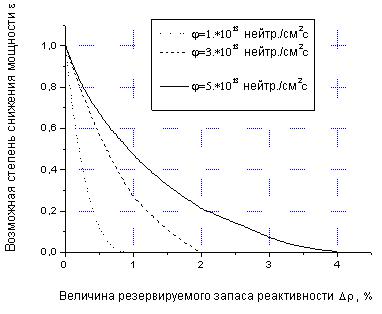
реакторов с нелинейной зависимостью ε(∆ρ) рассмотрено в разд. 4.2.)

Рис. 2.1. Зависимость возможной степени снижения мощности от величины резервируемого запаса реактивности

2.2.2.Оптимальное распределение запасов реактивности

всистеме реакторов с линейной зависимостью возможной степени снижения мощности от запаса реактивности

Вэтом случае математическая постановка задачи такова: найти

min ∑N ∆ρi

∆ρi i=1 ai

при ограничениях:

118

N
∑δi εi (∆ρi ) = α;	(2.20)
i=1
0 ≤ ∆ρi ≤ ∆ρi m ,	i =1, ..., N,

где εi = 1 − Ki ∆ρi .

Как видно из соотношения (2.20) оптимизационная задача относится к классу задач линейного программирования и может быть решена симплекс-методам (см. разд. 1.2). Однако вследствие того, что задача содержит всего одно уравнение связи между переменными, она может быть решена для произвольного числа реакторов, входящих в систему, достаточно просто без применения ЭВМ [66].

Решение задачи. Графическая интерпретация. Введем для удобства новые переменные

zi =	∆ρi	, i =1, ..., N,
	∆ρi м

имеющие смысл относительных запасов реактивности. Примем во внимание, что в широком диапазоне изменения плотностей потоков

	ϕ > 6	÷ 7 10	12	нейтр.			∆ρм (ϕ) линейна,
нейтронов						зависимость
				см2
					с

т.е. ∆ρм = b ϕ, где b = const.

Запишем оптимизационную задачу (2.20) для новых переменных:

найти

	N	ϕ	i zi
min ∑
z1...zN i=1		ai
при ограничениях:
N
∑δi (1	− zi ) = α;			(2.21)
i=1

0 ≤ zi ≤1 i =1, ..., N.

N

Учитывая, что ∑δi =1 , и обозначив

i=1

119

yi = δi zi ,

µi = δϕi ai i ,

приведем оптимизационную задачу (2.21) к стандартному виду задач линейного программирования:

найти

		N
zmin...z		∑µi yi
1	N i=1
при ограничениях:
N
∑δi (1	− zi ) = α;		(2.22)
i=1
0 ≤ zi ≤1		i =1, ..., N.

Перенумеруем реакторы, входящие в систему, в порядке возрастания коэффициентов µi .

N

Пусть 1− α ≤ δ1 , тогда ясно, что сумма S = ∑µi yi минимальна,

i=1

если

y1 =1− α, y2 = ... = yi = ... = yN = 0.

Действительно, если распределение {yi } имеет любой другой вид, например

y1 = γ1, y2 = γ2 , ..., yN	=1− α − N∑−1γi ,	причем γ1 =1− α,
	i=1
N
то минимизируемая сумма ∑µi yi имеет величину
i=1
		N −1
S'= µ1γ1 + µ2 γ2				,
	+... + µN 1− α − ∑γi
		i=1
при оптимальном же распределении
		N −1
S'= µ1γ1 + µ1γ2
	+... + µ1 1− α − ∑γi		.
		i=1

120