Загребаев Методы матпрограммирования 2007

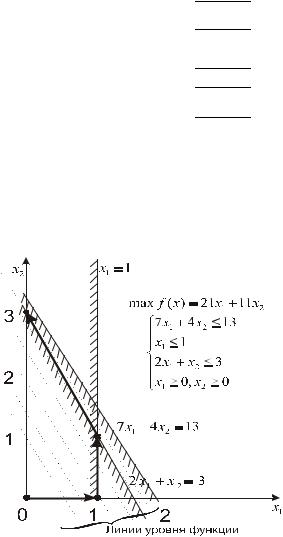
6. Составим табл. 1.7, которая образуется при удалении из базиса элемента x1 и ввода в базис элемента x4 .

						Таблица 1.7
Базис	Свободный	x1	x2	x3	x4		x5
	член
x3	1	–1	0	1	0		–4
x4	1	1	0	0	1		0
x2	3	2	1	0	0		1
f (x)	33	1	0	0	0		11

Поскольку в последней строке табл. 1.7 отрицательных коэффициентов нет, то процесс решения задач закончен. При этом x1 = 0 ,

x2 = 3 , x3 =1, x4 =1 , x5 = 0 ( x1, x5 – свободные переменные). Оптимальное значение целевой функции – f (x) = 33 .

Геометрическая интерпретация решения задачи представлена на рис. 1.5.

Рис. 1.5. Геометрическое представление задачи

31

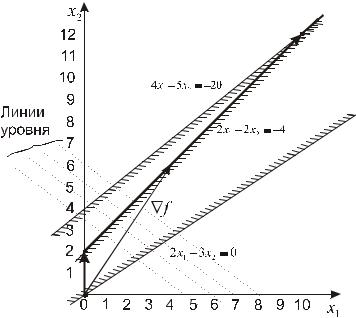
Задача 2. Найти max функции f (x) = 3 + 4x1 + 6x2 при ограничениях:

2x1 − 3x2 ≤ 0;

2x1 − 2x2 ≥ −4;4x1 − 5x2 ≥ −20;

x1 ≥ 0, x2 ≥ 0.

Геометрическая интерпретация задачи 2 приведена на рис. 1.6.

Рис. 1.6. Геометрическое представление задачи 2

Решение будем проводить в соответствии с порядком, изложенным при решении предыдущей задачи.

2x1 − 3x2 + x3 = 0,
1. 2x1 − 2x2 − x4 = −4, r = 3 .
4x − 5x		2	− x	5	= −20.
	1

32

2.x3 , x4 , x5 – базисные; x1 , x2 – свободные

x3 = 0 − 2x1 + 3x2 ;
x4 = 4 + 2x1 − 2x2 ;							f (x) = 3 + 4x1 + 6x2 – целевая функция.
x	5	= 20 + 4x		− 5x	2	;
			1
Составим соответствующие табл. 1.8 – 1.10.
													Таблица 1.8
Базис			Свободный				x1		x2		x3	x4		x5
			член
		x3		0			2		–3		1	0		0
		x4		4			–2		2		0	1		0
		x5	20				–4		5		0	0		1
	f (x)			3			–4		–6		0	0		0
													Таблица 1.9
Базис			Свободный				x1		x2		x3	x4		x5
			член
		x3		6			–1		0		1	3/2		0
		x2		2			–1		1		0	1/2		0
		x5	10				1		0		0	–5/2		1
	f (x)		15				–10		0		0	3		0
													Таблица 1.10
Базис			Свободный				x1		x2		x3	x4		x5
			член
		x3	16				0		0		1	–1		1
		x2	12				0		1		0	–2		1
		x1	10				1		0		0	–5/2		1
	f (x)		115				0		0		0	–-28		10
Как видно, в табл. 1.10 все αij									< 0	( j = 4) . Следовательно, зада-

ча не имеет решения.

33

Задача 3. Найти max функции f (x) = 2 + 4x1 + 2x2 + 2x3 при ограничениях:

2x1 − 3x2 +15x3 ≤ 3;2x1 + 2x2 + 8x3 ≤ 32;2x1 − 4x2 +16x3 ≤ 2;

x1 ≥ 0, x2 ≥ 0, x3 ≥ 0.

Решение будем проводить в соответствии с порядком, изложенным при решении задач 1 и 2.

2x1 − 3x2 +15x3 + x4 = 3;

1.

2x1

+ 2x2

+ 8x3 + x5 = 32;

r = 3 .

2x

− 4x

2

+16x

3

+ x

6

= 2,

1

x4

= 3 − (2x1 − 3x2 +15x3 );

2.

x5 = 32 − (2x1 + 2x2 + 8x3 );

f (x) = 2 − (−4x1 − 2x2 − 2x3 ).

x

6

= 2 − (2x − 4x

2

+16x

3

),

1

Составим соответствующие табл. 1.11 – 1.14.

									Таблица 1.11
Базис	Свободный		x1		x2	x3	x4	x5		x6
	член
x4	3	2			–3	15	1	0		0
x5	32	2		2		8	0	1		0
x6	2		2		–4	16	0	0		1
f (x)	2		–4		–2	–2	0	0		0
									Таблица 1.12
Базис	Свободный		x1		x2	x3	x4	x5		x6
	член
x4	1	0			1	–1	1	0		–1
x5	30	0		6		-8	0	1		–1
x1	1	1			–2	8	0	0		1/2
f (x)	6	0			–10	30	0	0		2

34

								Таблица 1.13
Базис			Свободный	x1	x2	x3	x4	x5		x6
			член
x2			1	0	1	–1	1	0		–1
x5			24	0	0	–2	–6	1		–5
x1			3	1	0	6	2	0		–3/2
f (x)			16	0	0	20	10	0		–8
								Таблица 1.14
Базис			Свободный	x1	x2	x3	x4	x5		x6
			член
x2			19/5	0	1	–7/5	–1/5	1/5	0
x6			24/5	0	0	–2/5	–6/5	1/5	1
x1			51/5	1	0	32/5	1/5	3/10	0
f (		)	272/5	0	0	84/5	2/5	8/5	0
	x

В соответствии с пунктом 3 алгоритма все γ j > 0 , значит, дос-

тигнуто оптимальное решение. Таким образом, имеем:

x1 = 515 , x2 = 195 , x3 = 0 , x4 = 0 , x5 = 0 , x6 = 245 ( x3 , x4 , x5 – свободные переменные).

Оптимальное значение целевой функции – f (x) = 54 52 .

1.3.Вырожденные задачи линейного программирования

1.3.1.Понятия вырожденности и зацикливания решения задач линейного программирования

Определение 1. Если хотя бы одно базисное решение xбi вы-

рожденное, то задача линейного программирования называется вырожденной, если все базисные решения xбi – невырожденные, то

задачу называют невырожденной.

35

Определение 2. Базисное решение xбi = (x1 , K, xr , K, xn ) на-

зывается невырожденным, если оно имеет точно r ( r = m – ранг системы ограничений) положительных координат. Если число положительных координат базисного решения меньше r , то решение называется вырожденным.

Пример. Рассмотрим задачу 2 из примера 1.2, которая не имеет решения.

Найти max f (x) = 3 + 4x1 + 6x2 . Система ограничений имеет вид:

x3 = 0 − (2x1 − 3x2 );
x4 = 4 − (2x1 − 3x2 );
x5 = 20 − (2x1 − 3x2 );	r = 3.

Первое базисное решение – вырожденное.

x3	= 0;
x4	= 4;		– базисное решение;
x5	= 20

x1 = 0; x2 = 0; x3 = 0

– свободные переменные.

Следовательно, по определению 1, задача – вырожденная (при решении этой задачи симплекс-методом, мы не столкнулись ни с какими особенностями; то что у задачи нет решения с вырожденностью никак не связано).

Рассмотрим ситуации, когда задача может обладать вырожденными базисными решениями.

1. Если ранг матрицы A меньше m (r < m) , то все базисные

решения задачи – вырожденные. Это не страшно, так как вырожденные задачи линейного программирования решаются не сложнее невырожденных. Такую ситуацию легко исключить, отбросив «лишние» уравнения.

2. Если ранг матрицы A равен m (r = m) ,то задача также может обладать вырожденными базисными решениями (см. пример), при-

36

чем это может обнаружиться не на первой итерации симплексметода, а позже.

К чему может привести применение симплекс-метода, если он попал в вырожденную точку?

Возможна (но необязательна) ситуация, когда симплекс-таблица принимает вид табл. 1.15.

Базис	Свободный
	член
x1	β1 > 0
.		.
.		.
.		.
xi	βi	= 0
.		.
.		.
.		.
xr	βr	> 0
f (x)		γ0

	x1	...	x j	...	xn
	α11	...	α1 j	...	α1n
	.	...	.	...	.
	.	...	.	...	.
	.	...	.	...	.
	.	...		...
	.	...	αij >0	...	αin
	.	...		...
	.	...	.	...	.
	.	...	.	...	.
	.	...	.	...	.
	.	...	αrj	...	αrn
	γ j	...	γ j	...	γn

Таблица 1.15

Примечание

Коэффициент αij будет раз-

решающим
элементом,		так
как	отношение
(β i	α ij = 0 )	–

минимально

γ j < 0 – ко-

эффициент, который выбираем

В результате получим следующее текущее базисное решение: x1 =β1 , ..., xi = 0, ..., xr = βr , xr +1 = x j =... = xn = 0 .

После изменения таблицы в соответствии с симплекс-методом базисное решение имеет вид.

x1 = β1 , ..., x j = 0, ..., xr = βr , xr +1 = 0, ..., xi = 0, ..., xn = 0 .

Таким образом, новое базисное решение совпадает с предыдущим (в столбце «свободный член» ничего не изменилось). Резуль-

37

татом итерации явилось то, что изменился базис точки. При этом значение целевой функции ( f (x) = γ0 ), естественно, не увеличи-

лось. (Коэффициенты αij и γ j изменились.)

Вычисления можно продолжать, надеясь, что в ходе очередной итерации удастся увеличить значение целевой функции, при этом возможно повторение нескольких «холостых» итераций.

Поскольку число различных базисов любого базисного решения – конечно, то после некоторого числа «холостых» итераций либо:

1)выяснится, что базисное решение, на котором мы «застряли» – оптимально;

2)обнаружится, что целевая функция задачи не ограничена сверху на допустимом множестве;

3)получится новое базисное решение;

4)мы придем к базису текущей точки, который уже фигурировал на одной из предыдущих итераций.

В отличие от благополучных случаев 1, 2 и 3, случай 4 означает, что мы вернемся к состоянию (с той же самой симплекс-таблицей),

вкотором уже были, и, следовательно, проходя снова и снова через тот же самый ряд пустых итераций, будем возвращаться в это же положение. Такое явление называют зацикливанием процесса решения задачи.

Из опыта применения симплекс-метода для исследования моделей реальных явлений сложилось убеждение, что вероятность зацикливания ничтожно мала. Известно лишь несколько специально разработанных задач линейного программирования, в процессе решения которых возникает зацикливание. Поэтому, поскольку зацикливание хотя и маловероятно, но все же возможно, необходимо уметь его устранять.

Оказывается, зацикливание можно предупредить, если внести в симплекс-алгоритм определенные уточнения относительно правила выбора разрешающего элемента. Любое правило выбора разрешающего элемента, с помощью которого можно избежать зацикливания, называют антициклином. Имеется несколько причем достаточно простых антициклинов. Остановимся на одном из них.

38

1.3.2. Антициклин

Легко доказывается тот факт, что в невырожденной задаче ми-

нимум отношения	βi	достигается на единственном номере l .
	αlj

Следовательно, номер переменной, которая выводится из числа базисных переменных – xl , и разрешающий элемент – αlj в невы-

рожденных задачах определяется однозначно. В вырожденных задачах это не так, т.е. может быть несколько минимальных отноше-

ний		βi		. Предположим,						что			на				очередной						итерации					симплекс-
	αij
таблица имеет вид табл. 1.16.
																												Таблица 1.16
Базис			Свобод-				x1	...				xr					xr +1		...					x j				...	xn
			ный член
x1				β1 > 0			1	...				α1r					α1r +1		...					α1 j				...	α1n
.						.	.	...				.					.		...						.			...	.
.						.	.	...				.					.		...						.			...	.
.						.	.	...				.					.		...						.			...	.
xl			βl			> 0	0	...				0					αl r +1		...				αl		j	> 0		...	αl n
1			1					...									1		...					1				...	1
.						.	.					.					.								.				.
.						.	.	...				.					.		...						.			...	.
.						.	.	...				.					.		...						.			...	.
xl			βl		2	> 0	0	...				0					αl2r +1		...				αl	2	j	> 0		...	αl	n
2																													2
.						.	.	...				.					.		...									...	.
																									.
.						.	.	...				.					.		...						.			...	.
.						.	.	...				.					.		...						.			...	..
xr				βr		> 0	0	...				1					αrr +1		...					αrj				...	αrn
f (x)					γ0		0	...				0					γr +1		...				γ j		< 0			...	γn
Предположим, что
									βl			βl		2					β	i
									1	=							= min				.
									αl1 j			αl2 j
																	αij >0		αij

39

Следовательно, нет однозначного выбора разрешающего элемента. Предположим, что мы произвольно выбрали l = l1 . Тогда после

преобразования таблицы на месте свободного члена βl2 появится нуль:

βl

βl

2

βl

β

l2

−

1

α

l2 j

=

−

1

α

l2 j

= 0 .

α

α

α

l1 j

l2 j

l1 j

Таким образом, появится вырожденное базисное решение и станет возможным зацикливание (Теперь ясно, почему в невырожденной задаче может быть только одно минимальное отношение.)

Доказано [ ], что зацикливание не может возникнуть, если на каждой итерации номер l -й переменной, выводимой из базиса, в случае неоднозначности, выбирать по следующему правилу.

Пусть имеем:

Q0 = min	β	i		βl		β	lk
			=	1	= ... =
				αl1 j		αlk j
αij >0	αij

(т.е. минимум достигается на номерах k > 1).

Надо вычислить отношения	αi1 для i = l	, ..., l	k	(т.е. вместо β	i
	1
	αij

из столбца свободных членов брать αi1 из первого столбца,										кото-
рый соответствует x ) и найти среди них min Q1 = min							αi1		.
		1				i=l1...lk	αij
Если минимум		Q1	достигается только для одного номера из
l1 , ..., lk	(например,	l2 ), то вопрос решен – xl2 выводится из бази-
са, αl2 j	– разрешающий элемент.
Если минимум Q1			достигается более чем для одного номера, то
для всех этих номеров			l ...l	s	(s ≤ k) находится Q 2	= min		αi2			(ко-
			1			i=l1...ls αij

эффициенты из второго столбца). И так далее.

Гарантируется, что найдется такое q (1 ≤ q ≤ n), для которого минимальное значение Qq достигается только для одного номера l .

40