Загребаев Методы матпрограммирования 2007

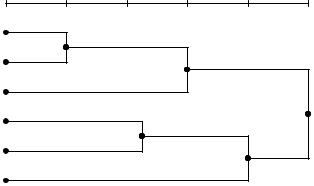
1,0	0,9	0,8	0,7	0,6	0,5	Сходство
0,0	0,1	0,2	0,3	0,4	0,5	Расстояние

Номер

объекта

1

3

6

5

4

2

Рис. 2.6. Пример дендограммы

Выполнение метода начинается с того, что каждый объект в выборке считается монокластером – кластером, состоящим из одного объекта. Далее последовательно «ослабляется» критерий о том, какие объекты являются уникальными, а какие нет. Другими словами, понижается порог, относящийся к решению об объединении двух или более объектов в один кластер. В результате, связывается вместе всё большее и большее число объектов и агрегируется (объединяется) все больше и больше кластеров, состоящих из все сильнее различающихся элементов. Окончательно, на последнем шаге все объекты объединяются вместе.

На первом шаге, когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Однако когда связываются вместе несколько объектов, возникает вопрос об определении расстояния между кластерами. Необходимо правило объединения или связи для двух кластеров. Можно связать два кластера вместе, когда любые два объекта в двух кластерах ближе друг к другу, чем соответствующее расстояние связи: используется «правило ближайшего соседа» для определения расстояния между кластерами; этот метод называется методом одиночной связи. Это правило строит «волокнистые» кластеры, т.е. кластеры, «сцепленные вместе» только отдельными элементами, случайно оказавшимися ближе остальных друг к другу.

141

Как альтернативу можно использовать соседей в кластерах, которые находятся дальше всех остальных пар объектов друг от друга. Этот метод называется методом полной связи. Существует также множество других методов объединения кластеров, основанных на различных подходах к объединению кластеров. Наиболее часто встречающиеся варианты иерархической кластеризации рассмотрены ниже.

Одиночная связь (метод ближайшего соседа). Как было опи-

сано выше, в этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Это правило должно, в известном смысле, «нанизывать» объекты вместе для формирования кластеров, и результирующие кластеры имеют тенденцию быть представленными длинными «цепочками».

Полная связь (метод наиболее удаленных соседей). В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах («наиболее удаленными соседями»). Этот метод обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных «рощ». Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.

Невзвешенное попарное среднее. В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные «рощи», однако он работает одинаково хорошо и в случаях протяженных («цепочного» типа) кластеров. Снит и Сокэл вводят аббревиатуру UPGMA для ссылки на этот метод, как на метод невзвешенного попарного арифметического среднего – unweighted pairgroup method using arithmetic averages.

Взвешенное попарное среднее. Метод идентичен методу не-

взвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому предлагаемый метод должен быть использован (скорее даже, чем предыдущий), когда предполагаются неравные размеры кластеров. Снит и Сокэл вводят аббревиатуру WPGMA

142

для ссылки на этот метод, как на метод взвешенного попарного арифметического среднего – weighted pair-group method using arithmetic averages.

Невзвешенный центроидный метод. В этом методе расстоя-

ние между двумя кластерами определяется как расстояние между их центрами тяжести. Снит и Сокэл используют аббревиатуру UPGMC для ссылки на этот метод, как на метод невзвешенного попарного центроидного усреднения – unweighted pair-group method using the centroid average.

Взвешенный центроидный метод (медиана). Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учёта разницы между размерами кластеров (т.е. числами объектов в них). Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего. Снит и Сокэл использовали аббревиатуру WPGMC для ссылок на него, как на метод взвешенного попарного центроидного усреднения – weighted pair-group method using the centroid average.

Метод Варда. Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. Метод является очень эффективным, однако он стремится создавать кластеры малого размера.

Кновым приближенным методам кластериации можно отнести

инейросетевые подходы. Рассмотрим их возможности на примере достаточно часто применяемой нейросети Кохонена. Нейросеть (НС) Кохонена относится к нейросетям без учителя. Это означает, что подстройка весов нейронов (обучение) такой сети производится исключительно на основе поступающих на ее вход данных. В традиционной нейросети без учителя используется т.н. соревновательное обучение, при этом выходы сети максимально скоррелированы: при любом значении входа активность всех нейронов, кроме нейрона-победителя, одинакова и равна нулю. Такой режим функционирования сети называется победитель забирает все.

Нейрон-победитель (с индексом i ), свой для каждого входного вектора, будет служить прототипом этого вектора. Поэтому побе-

143

дитель выбирается так, что его вектор весов wi , определенный в том же d -мерном пространстве, находится ближе к данному входному вектору x , чем у всех остальных нейронов: wi − x ≤ wi − x

для всех i. Если, как это обычно и делается, применять правила обучения нейронов, обеспечивающие одинаковую нормировку всех

весов, например, wi =1, то победителем окажется нейрон, дающий наибольший отклик на данный входной стимул: wi x ≥ wi x i . Выход такого нейрона усиливается до единич-

ного, а остальных – подавляется до нуля.

Количество нейронов в соревновательном слое определяет максимальное разнообразие выходов и выбирается в соответствии с требуемой степенью детализации входной информации. Обученная сеть может затем классифицировать входы: нейрон-победитель определяет, к какому классу относится данный входной вектор.

По предъявлении очередного примера корректируются лишь веса нейрона-победителя

∆w τ	= η(xτ − w		) .	(2.43)
i		i
Здесь η – скорость обучения;		wi	– вектор	весов нейрона-

победителя; xτ – предъявленный пример.

Описанный выше базовый алгоритм обучения на практике обычно несколько модифицируют, так как он, например, допускает существование так называемых мертвых нейронов, которые никогда не выигрывают, и, следовательно, бесполезны. Самый простой способ избежать их появления – выбирать в качестве начальных значений весов случайно выбранные в обучающей выборке входные вектора. Такой способ хорош еще и тем, что при достаточно большом числе прототипов он способствует равной «нагрузке» всех нейронов-прототипов. Это соответствует максимизации энтропии выходов в случае соревновательного слоя. В идеале каждый из нейронов соревновательного слоя должен одинаково часто становились победителем, чтобы априори невозможно было бы предсказать, какой из них победит при случайном выборе входного вектора из обучающей выборки.

144

Наиболее быструю сходимость обеспечивает пакетный (batch) режим обучения, когда веса изменяются лишь после предъявления всех примеров. В этом случае можно сделать приращения не малыми, помещая вес нейрона на следующем шаге сразу в центр тяжести всех входных векторов, относящихся к его ячейке. Такой алгоритм сходится за O(1) итераций.

Записав правило соревновательного обучения в градиентном

∂E

виде: < ∆w >= −η ∂w , легко убедиться, что оно минимизирует

квадратичное отклонение входных векторов от их прототипов – весов нейронов-победителей:

	E =	1	∑α		xα − w α		.	(2.44)
		2

Иными словами, сеть осуществляет кластеризацию данных: находит такие усредненные прототипы, которые минимизируют ошибку огрубления данных. Недостаток такого варианта кластеризации очевиден – «навязывание» количества кластеров, равного числу нейронов.

Один из вариантов модификации базового правила обучения соревновательного слоя состоит в том, чтобы обучать не только ней- рон-победитель, но и его «соседи», хотя и с меньшей скоростью. Такой подход – «подтягивание» ближайших к победителю нейронов – применяется в топографических картах Кохонена (Kohonen, 1982). Небольшой модификацией соревновательного обучения можно добиться того, что положение нейрона в выходном слое будет коррелировать с положением прототипов в многомерном пространстве входов сети: близким нейронам будут соответствовать близкие значения входов. Тем самым, появляется возможность строить топографические карты, чрезвычайно полезные для визуализации многомерной информации. Обычно для этого используют соревновательные слои в виде двумерных сеток. Такой подход сочетает квантование данных с отображением, понижающим размерность. Причем это достигается с помощью всего лишь одного слоя нейронов, что существенно облегчает обучение.

Нейроны выходного слоя упорядочиваются, образуя одноили двумерные решетки, т.е. теперь положение нейронов в такой решетке маркируется векторным индексом i . Такое упорядочение

145

естественным образом вводит расстояние между нейронами i − j в

слое. Модифицированное Кохоненом правило соревновательного обучения учитывает расстояние нейронов от нейрона-победителя:

∆w iτ = ηΛ(

i − i

) (xτ − wi ) .

(2.45)

Функция соседства Λ( i − i ) равна единице для нейрона-

победителя с индексом i и постепенно спадает с расстоянием, например по закону Λ(a) = exp (−a2 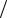σ2 ) . Как темп обучения η, так

и радиус взаимодействия нейронов σ постепенно уменьшаются в процессе обучения, так что на конечной стадии обучения мы возвращаемся к базовому правилу адаптации весов только нейроновпобедителей.

После обучения нейросети Кохонена вектора весов нейронов единственного слоя представляют собой ни что иное, как центры кластеров. Принадлежность объекта кластеризуемого множества к определенному кластеру определяется близостью вектора объекта к вектору весов нейрона.

Тестовые множества могут различаться одним или несколькими из следующих параметров: размерность пространства дескрипторов (П-пространства) d; общее количество кластеризуемых объектов N.

Основные характеристики компьютера, на котором проводилось тестирование, приведены в табл. 2.2.

	Таблица 2.2
Название параметра	Значение параметра
Процессор	AMD Athlon 1200 МГц
Объем и тип оперативной памяти	512 МБ DDR-266
Операционная система	Windows 2000 Professional SP3

Параметры тестовых множеств, представлены в табл. 2.3.

	Таблица 2.3
Название параметра	Значение параметра
Диапазон значений параметра	[0; 10]
Распределение значений в диапазоне	равномерное

146

Настройки для методов кластеризации UPGMC и НС Кохонена приведены в табл. 2.4.

Отметим, что для каждой серии экспериментов число кластеров необходимо задавать, явно (НС Кохонена) или неявно (UPGMC). Для НС Кохонена число нейронов в слое является ограничением сверху числа кластеров и одновременно наиболее вероятным (по данным экспериментов) числом выделяемых кластеров. В некоторых случаях нейросеть Кохонена с N нейронами в единственном слое выделяет N – 1 кластер, что можно отметить как положительное свойство НС учитывать реальную структуру данных.

					Таблица 2.4
	Название параметра				Значение параметра
Активационная функция нейронов НС					Линейная: f(x) = x
Кохонена
Число нейронов в слое НС Кохонена					равно заданному числу кластеров
Начальные веса слоя НС Кохонена					Случайно выбранные объекты кла-
					стеризуемого множества
Точность обучения НС Кохонена					0,01
Начальный		радиус	взаимодействия		1,0
нейронов
Коэффициент		изменения		радиуса	0,9
взаимодействия
Начальная скорость обучения					1,0
Коэффициент		изменения		скорости	1,0
обучения
Пакетный режим обучения					Да
Критическое расстояние UPGMC					Для получения заданного числа
					кластеров
Частота	обновления		информации,		100
1/итер

На основе известного тестового множества подбирается критическое расстояние UPGMC для получения заданного числа класте-

147

ров. Затем найденное расстояние используется для проведения эксперимента.

Для НС Кохонена проводилось по три эксперимента с различными начальными приближениями, и в качестве результата бралось среднее арифметическое. Используются следующие обозначения для критериев оценки качества кластеризации: полная сумма внутрикластерных расстояний – ПСВКР; сумма квадратов отклонений от центра кластера – СКО.

2.3.5. Зависимость времени и качества кластеризации от количества объектов, кластеров и размерности признакового пространства

Положим число кластеров m = 5, размерность признакового пространства d = 3. Результаты испытаний приведены в табл. 2.6 и

на рис. 2.7, 2.8.

				Таблица 2.6
Параметр	Количество кластеризуемых объектов
	10	50	75		100
Время UPGMC, мин:с, мс	00:00.019	00:04.325	00:41.000		03:42.000
Время НС Кохонена, мин:с, мс	00:00.060	00:00.477	00:00.811		00:01.191
Полная сумма внутрикластер-	24	1134	2867		9673
ных расстояний UPGMC
Полная сумма внутрикластер-	28	903	1989		4412
ных расстояний НС Кохонена
Сумма квадратов отклонений	30	440	784		1427
UPGMC
Сумма квадратов отклонений	45	335	508		900
НС Кохонена

148

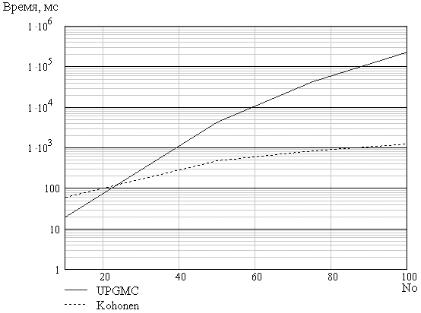
Рис. 2.7. Зависимость времени кластеризации от количества объектов

Как видно из рис. 2.11, время кластеризации для обоих алгоритмов растет экспоненциально, однако для алгоритма НС Кохонена коэффициент роста значительно ниже, в результате уже примерно при 25 объектах в кластеризуемом множестве метод UPGMC начинает проигрывать по времени. Из рисунков видно, что во всех случаях НС Кохонена дает лучшее значение обоих критериев.

В данном эксперименте положим число объектов в кластеризуемом множестве N = 50, размерность признакового пространства d = 3. Будем кластеризовать одно и то же множество для получения разного количества кластеров (напомним, что оно задается числом нейронов в слое НС Кохонена и неявно – критическим расстоянием в UPGMC). Результаты испытаний приведены в табл. 2.7.

Как следует из рис. 2.9, время кластеризации для метода UPGMC практически не зависит от количества кластеров (это подтверждается и теоретически, так как число итераций алгоритма невзвешенного попарного усреднения равно разности числа объектов кластеризуемого множества и количества выделяемых методом

149

кластеров). Для НС Кохонена наблюдается примерно экспоненциальный рост, связанный с тем, что количество выделяемых НС кластеров определяется числом нейронов в единственном слое; следовательно, при одном и том же числе объектов в кластеризуемом множестве увеличение числа нейронов увеличивает также и число операций на каждой итерации алгоритма нейросетевой кластеризации.

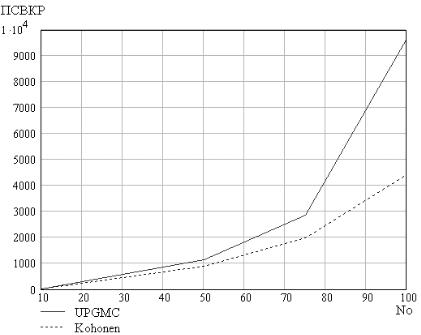
Рис. 2.8. Зависимость значения критерия качества от количества объектов (ПСВКР)

Рис. 2.10 и 2.11 показывают превосходство алгоритма НС Кохонена по качеству кластеризации над методом UPGMC.

Зависимость времени и качества кластеризации от размерности пространства исследовалась при следующих условиях: количество кластеров m = 5, число объектов в кластеризуемом множестве N = 50. Результаты приведены в табл. 2.8.

150