Загребаев Методы матпрограммирования 2007

												Таблица 1.31
								B
A
	B1		B2				B3			B4			Запасы ai
A1	5				7				1		3
														80	/ 20
	60	20
A2	4				8				4		2
		20				70								90	/ 70
A3	1				5	20			6	70	9		90
Заявки b j	60			/ 20				/ 20		70			260
			40				90

Можно показать, что диагональный метод всегда приводит к опорному допустимому решению. Однако следует иметь в виду, что поскольку данный метод не учитывает стоимость перевозок, то опорные планы, полученные с его помощью, значительно отличаются от оптимальных.

Метод минимального элемента дает возможность учесть за-

данные стоимости. От диагонального метода он отличается только тем, что в таблице выбирается не верхняя левая клетка, а клетка с минимальной стоимостью cij , и как в диагональном методе в эту

клетку записывается минимальное из двух чисел a1 и b1 , т.е. min{a1, b1} . Затем соответствующий столбец или строка из табли-

цы вычеркивается и т.д.

Пример 2. Рассмотрим табл. 1.32.

											Таблица 1.32
A
	B1		B2			B3			B4			Запасы ai
A1	5	7			80			1		3	80
A2	4	8						4		2		90 / 20			/ 10
		10			10				70
A3	1	5			6					9			90	/ 30
	60	30
Заявки b j	60		40	/ 10		90	/ 10		70		260

71

В соответствии с опорным планом, полученным данным методом, значение функции

3 4

f (x) = ∑ ∑cij xij = 550.

i=1 j=1

Опыт решения транспортных задач показал, что далеко не всегда использование метода минимального элемента, вместо диагонального, дает лучшее приближение к оптимальному решению.

1.6.3. Метод потенциалов

Это основной метод решения транспортной задачи. Метод базируется на ряде теорем, которые рассмотрим ниже.

Введем понятие псевдостоимости.

Пусть за перевозку единицы груза с базы Ai вносится плата αi , а за перевозку единицы груза на базу B j – плата β j . Псевдостои-

мостью перевозки из Ai в B j	~				= αi + β j .
	называется сумма cij
Совокупность величин	(αi ,β j ), i =		, j =			называется
		1, m		1, n,

платежами, или потенциалами.

Теорема о платежах. Для заданной совокупности платежей суммарная псевдостоимость перевозки при любом допустимом плане xij сохраняет одно и то же значение, т. е.

			~	m	n ~
			f (x)	= ∑∑cij xij = const .
				i=1 j=1
Доказательство.
~	m n	~	m n			m n	m n
f (x) = ∑∑cij xij			= ∑∑(αi		+β j )xij = ∑∑αi xij + ∑∑β j xij =
	i=1 j=1		i=1 j=1			i=1 j=1	i=1 j=1
	m	n	n	m	m	n
	= ∑αi	∑xij + ∑β j ∑xij = ∑				αi ai + ∑β jb j = const.
	i=1	j=1	j=1 i=1		i=1	j=1

Так как план – допустимый, то выполняются соотношения:

72

m

∑xij = ai ,

i=1

n

∑xij = b j , j =1

при этом суммарная псевдостоимость перевозки не зависит от пла-

~

на xij , т.е. f (x) = const . Таким образом, теорема доказана.

Теорема об оптимальности. Если для всех базисных клеток (xij > 0) псевдостоимость равна стоимости, т.е. c~ij = cij , а для сво-

бодных клеток (xij = 0) выполняется неравенство с~ij ≤ cij , то план

является оптимальным и никаким способом не может быть улучшен.

Доказательство. Для базисных клеток имеем

m n	m n	~	~
f (x) = ∑∑cij xij = ∑∑cij xij =			f (x) = const .
i=1 j=1	i=1 j=1

Заменим план xij на любой другой допустимый план xij′ . Тогда получим другое значение целевой функции

m n

f (x′) = ∑∑cij xij′ . i=1 j=1

В базисных клетках, которые сохранились от старого плана, стоимость сij = c~ij , а в базисных клетках нового плана, которые в

плане xij были свободными, стоимость сij ≥ c~ij . Следовательно,

		m n	~	= const =	~
		f (x′)≥ ∑∑cij xij′			f (x′) ,
	~	i=1 j=1
′		′
т.е. f (x ) ≥	f (x ) .

Таким образом, при любом плане, отличном от xij , функция f (x ′) может быть только больше. Значит, xij – оптимальный план. Теорема доказана.

73

Из условия равенства сij = c~ij в базисных клетках можно определить потенциалы αi и β j . В опорном плане (n + m −1) базисных клеток; причем значения cij известны. Для нахождения потенциалов составим систему уравнений, используя табл. 1.32:

α1 +β3 =1;

α2 +β3 = 4;

α2 +β2 = 8;

α3 +β2 = 5;

α3 +β1 =1;

α2 +β4 = 2.

Система имеет (n + m −1) уравнений и (n + m) неизвестных потенциалов. Для получения решения необходимо произвольно выбрать один из потенциалов, например α1 =1. Остальные потенциа-

лы однозначно определяются при решении системы уравнений:

β3 = 0 , α2 = 4 , β2 = 4 , α3 =1, β1 = 0 , β4 = −2 .

Следует отметить, что в системе потенциалов могут быть и отрицательные элементы.

Определив потенциалы, находят псевдостоимости c~ij = αi + β j

в остальных небазисных клетках и проставляют их в левом углу небазисных клеток (табл. 1.33).

									Таблица 1.33
					B
A
	B1		B2		B3		B4			αi
A1	1 < 5		6 < 7		80	1	–1 < 3			1
A2	4 ≤ 4		10	8	10	4	70	2		4
A3	60	1	30	5	1 < 6		–1 < 9			1
β j	0		4		0		–2

74

Далее проверяют, является ли опорный план оптимальным.

В рассматриваемом случае план является оптимальным, так как во всех небазисных клетках с~ij ≤ cij .

Возьмем другую таблицу, построенную диагональным методом

(табл. 1.34).

								Таблица 1.34
					B
A
	B1		B2		B3		B4		αi
A1	60	5	20	7	3 > 1		6 > 3		1
A2	6 > 4		20	8	70	4	7 > 2		2
A3	8 > 1		10 > 5		20	6	70	9	4
β j	4		6		2		5

Опорный план не является оптимальным, так как имеются клетки, где c~ij > cij .

Выбирается клетка с максимальной разностью ( ~31 − 31 = ). c c 7

Эта клетка берется за начальную для построения, так называемого, цикла пересчета, с помощью которого можно найти новый опорный план с меньшим значением целевой функции.

Циклом пересчета для данной свободной клетки называется замкнутая линия, все вершины которой, за исключением данной, лежат в базисных клетках. Вершинам цикла пересчета присваиваются знаки «+» или «–». Знаки последовательных вершин чередуются, причем свободная клетка имеет положительный знак. Доказано, что для каждой свободной клетки существует и притом единственный цикл пересчета.

Ценой цикла называется приращение стоимости перевозок при перемещении единицы груза по циклу, она равна алгебраической сумме стоимостей, стоящих в вершинах цикла, а, в конечном счете, равна:

γij = cij −c~ij .

75

Цена может быть как положительной, так и отрицательной.

Очевидно, γij < 0	~	> cij	и в этом случае стоимость перевозок
	при cij

уменьшается.

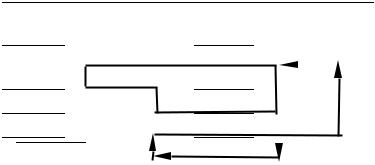
Некоторые циклы пересчета представлены в табл. 1.35.

Таблица 1.35

A

B

B1

B2

B3

B4

B5

B6

A

c11

–

c

c

c

+

c

–

c

1

12

13

14

+

15

16

A2

c21

+

c22

– c23

c24

c25

c26

A3

+ c31

–

c32

+

c33

c34

–

c35

c36

A4

c41

c42

– c43

c44

c45

+

c45

A

– c

51

+ c

52

+

c

53

c

54

–

c

55

c

56

5

Покажем справедливость того, что цена γij = ij − ~ij . c c

В соответствии с табл. 1.35 цена цикла для клетки (5, 3) определяется выражением:

γ53 = c53 − c43 + c46 − c16 + c15 − c55 =

= c53 − (α4 + β3 ) + (α4 + β6 ) − (α1 + β6 ) + (α1 + β5 ) − (α5 + β5 ) =

= c53 − (β3 + α5 ) = c53 − ~53 ,

c

что соответствует указанному выше утверждению.

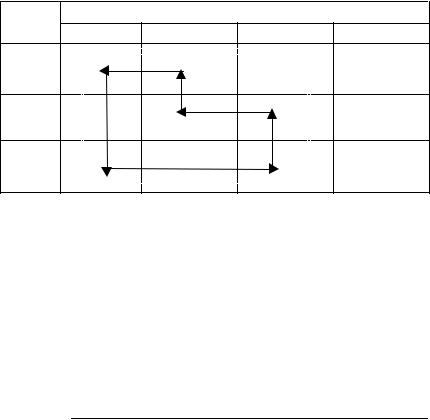
Рассмотрим пример, представленный табл. 1.36, элементы которой соответствуют элементам табл. 1.34.

Выберем клетку с максимальной разностью ~ij − ij , т.е. клетку c c

(3, 1), и построим для нее цикл пересчета. Прямая, выходящая из клетки, совершает повороты в базисных клетках и возвращается в начальную.

Теперь нужно перераспределить базисные переменные, находящиеся в вершинах цикла, так, чтобы в свободной клетке появилось положительное значение, а одна из базисных переменных приняла нулевое значение. При этом должно сохраниться требование, что все xij ≥ 0 . Доказано, что при таком перемещении будет получено

76

новое решение транспортной задачи с уменьшенным значением
целевой функции, если цена цикла γij						< 0 .
								Таблица 1.36
A						B
		B1		B2			B3	B4
A1		–	5	+	7		1	3
	60			20		3		6
A2			4		8		4	2
	6			–		70	+	7
				20
A3			1		5		6	9
	8	+		10		20	–	70

f(x) = 1630 .

Впримере наименьшее значение базисной переменной, которую можно переместить по циклу, равно 20. Таким образом, это число нужно прибавить к базисным переменным вершин цикла, имеющих знак «+», и вычесть из переменных в вершинах цикла со зна-

ком «–». В результате, в клетке (3, 1) появится переменная x31 = 20 . Значение переменной более 20 выбрать нельзя, так как

это приведет к появлению отрицательных значений xij . После перемещения по циклу получим табл. 1.37.

						Таблица 1.37
				B
	A
		B1	B2	B3	B4	ai
	A1	40	40			80
	A2		0 (ε)	90		90
	A3	20		0	70	90
	bj	60	40	90	70

f (x) = 1490 .

77

Новый опорный план соответствует меньшему значению целевой функции, причем уменьшение составляет величину γij xij

(7 20 =140), где xij – перемещенное по циклу число.

Следует отметить одну особенность полученной таблицы: вместо одной переменной нулю стали равны две переменные x22 , x33 . Это означает, что задача вырожденная, так как число базисных переменных меньше (n + m −1). Для устранения вырожденности предположим, что в одной из клеток, например в клетке (A2 , B2 ),

имеется бесконечно малая величина ε > 0 , которую в окончательном плане примем равной нулю.

Подводя итоги, сформулируем алгоритм решения транспорт-

ной задачи.

1.В качестве первого приближения берется допустимый план, полученный одним из методов нахождения начального опорного плана.

2.Для данного плана определяется система платежей исходя из условия, что в любой базисной клетке стоимость равна псевдостоимости.

3.Подсчитывается псевдостоимость для всех свободных клеток.

Если окажется, что для всех клеток плана с~ij ≤ cij , то задача ре-

шена, найденный план оптимален.

В противном случае, т.е. если существуют клетки, в которых c~ij > cij , переходим к шагу 4.

4. Для свободной клетки с максимальной разностью c~ij − cij > 0

строится цикл пересчета, после чего составляется новый опорный план и осуществляется переход на шаг 2.

Отметим, что логические операции, составляющие содержание процедуры поиска цикла, гораздо более экономны в смысле затрат времени ЭВМ по сравнению с арифметическими операциями сим- плекс-метода.

В заключение, обратим внимание на любопытную особенность транспортной задачи: если все числа ai , b j (i =1, m, j =1, n) –

целые, то любой опорный план транспортной задачи (в том числе оптимальный) – целочисленный.

78

Действительно, когда все числа ai , b j – целые, начальный

опорный план, полученный диагональным или другим методом, является целочисленным. Кроме того, на каждой итерации метода потенциалов перемещаемое число xij является целым, поэтому

любой следующий опорный план – целочисленный.

1.6.4. Транспортные задачи с неправильным балансом

Ранее был рассмотрен метод решения простейшей транспорт-

m	n
ной задачи в случае выполнения условия ∑ai = ∑b j , т.е. когда
i =1	j =1

суммарный объём возможных поставок равнялся суммарному объёму потребностей (закрытая транспортная задача). Между тем чаще возникают транспортные задачи, в которых условие баланса нарушено в ту или иную сторону (открытые транспортные задачи).

m		n
Так в случае, когда ∑ai	> ∑b j		задачу можно сформулировать
i =1		j =1
следующим образом:
найти
		m	n
min f (x) = ∑ ∑cij xij
		i=1	j=1
при ограничениях:
n
∑ xij		≤ ai , i =		1, m		;
j =1
m
∑ xij		= b j , j =			1, n.

i =1

Это означает, что у некоторых поставщиков остаётся неотправ-

	m	n
ленная продукция, суммарный объём которой равен	∑ai − ∑b j .
i=1		j=1

79

• Если безразлично, у каких именно поставщиков и в каких количествах останется продукция, то задача с неправильным балансом может быть сведена к эквивалентной ей задаче с правильным балансом, т.е. к закрытой транспортной задаче. Для этого вводится еще один фиктивный потребитель с заявкой

m	n
bn+1 = ∑ai − ∑b j
i =1	j =1

и стоимостью перевозок от каждого поставщика

ci n+1 = 0, i =1, m.

Тогда, поставленная задача может быть записана в виде: найти

	m	n+1
min f (x) = ∑ ∑cij xij
	i=1 j=1
при ограничениях:
n +1
∑ xij	= a i , i	=	1, m		;
j =1
m
∑ xij	= b j ,	j =		1, n + 1 .

i =1

Полученная задача действительно эквивалентна исходной, так как фиктивные перевозки не влияют на значение целевой функции, поскольку ci n+1 = 0.

Совершенно аналогично можно поступить в случае

m	n
∑ai	< ∑b j , т.е. когда продукции недостаточно для полного удов-
i=1	j=1

летворении потребностей. В этом случае вводится в рассмотрение фиктивный поставщик с объемом возможных поставок, равным

недостатку продукции		n	m
		∑b j − ∑ai . Стоимости перевозок от
	j=1		i=1

80