Коновалов Учебно-методическое пособие по курсу 2007

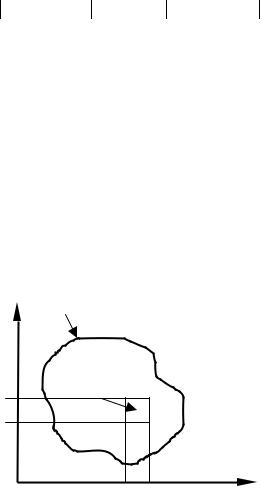
(рис. 2), верхняя и нижняя грани которого находятся на уровнях hs (x, y) и hb (x, y) , определяет изменение толщины льда в точке (x*, y*) за время ∆t :

ρ∆H ∆x ∆y = a0 ∆x∆y ∆t −

ρ∆t(∆y∫hhbs u x +∆x dz −∆y∫hhbs u x dz + ∆x∫hhbs v y +∆y dz −∆x∫hhbs v y dz),

где u и v – горизонтальные компоненты скорости течения льда, a0

– поток льда через единицу площади поверхности и основания ледникового покрова в единицу времени, учитывающий аккумуляцию и сезонное таяние на поверхности, а также придонное таяние в основании ледника.

Переходя к пределам ∆x, ∆y, ∆t → 0 , получим уравнение

баланса массы в ледниковом покрове, определяющее изменение формы ледника со временем:

	∂ H			r
		= a − div q ,				(8)
	∂t
где a = a0 / ρ ,			r	H	H
			q	= ∫u dz;	∫v dz .
				0	0

Уравнение (8) определяет эволюцию ледника и называется прогностическим уравнением.

Г

Ω

y+∆y

(x*,y*)

y

x x+∆x

Рис. 2. Область залегания ледникового покрова Ω с границей Γ

11

1.4. Уравнение переноса тепла

Изменение температуры льда со временем определяется уравнением переноса тепла [3]:

	∂T	r	r	r	′
						&
		+ (v
ρ с	∂t		, )T	=div (χ T ) +σik εik .

С учетом закона Глена (5) уравнение переноса тела в ледниковом покрове окончательно может быть записано в виде:

r

−

1

1+n

∂T

r

2 A

n

ε

n

(9)

+ (vr, )T = div (χ T ) +

.

&

∂t

ρ с

ρ c

§ 2. Приближение тонкого слоя льда. Приближенные аналитические решения для скорости течения льда

Рассмотрим плоскую	модель течения	льда (рис. 3). В
приближении тонкого слоя	H0 / L0 <<1, где	H0 – толщина

ледникового покрова в окрестности вершины, L0 – линейные

размеры основания. В таком приближении может быть получено выражение для горизонтальной составляющей скорости течения льда, основанное на законе Глена (2) и оценках производных компонент скорости течения, входящих в выражение для второго инварианта тензора скоростей деформаций.

12

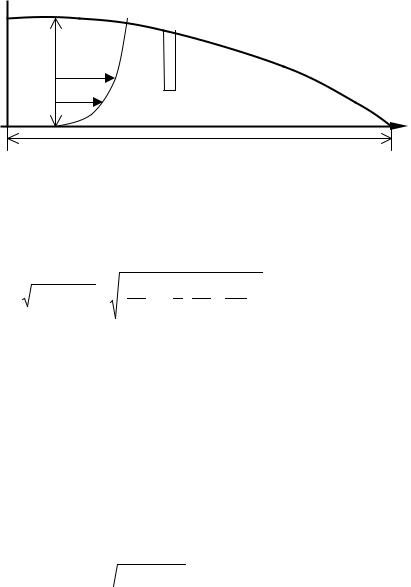
z

ur

H0

σ′xz

L0

x

Рис. 3. Геометрия течения ледника

В данном случае плоского течения, с учетом уравнения непрерывности для несжимаемой среды ( ε&xx +ε&zz = 0 ), второй

инвариант

тензора

скоростей

деформаций

&

& 2

&

2

∂u

2

1

∂u

∂w

2

=

+

+

,

w

– вертикальная

ε =

εxx

+εxz

4

∂ z

∂ x

∂ x

компонента скорости течения льда.

Пусть v0 – характерное значение скорости течения льда в ледниковом покрове. Тогда имеют место следующие оценки:

∂w

∂u

v0

∂u

v0

u′x

H

&

<

~

;

~

;

~

<<1 ;

εxx

<<1 . (10)

∂ x

∂ x

L

∂ z

H

′

L

&

uz

εxz

Следовательно, для второго инварианта тензора скоростей деформаций в приближении тонкого слоя имеет место равенство:

&	≈		&		≈	1	∂u	.
ε			εxz			2	∂ z

Для компонент девиатора напряжений с учетом уравнения непрерывности и соотношений (3) имеет место равенство

σ′xx = −σ′zz .

Соответственно,

второй

инвариант

девиатора

напряжений σ′ = σ′xx 2 +σ′zz 2 .

13

Принимая во внимание соотношение между компонентами тензора скоростей деформаций (10), получим

σ′xx

<<1 ;

σ′ ≈

σ′xz

.

σ′xz

Таким образом, закон Глена (2) принимает вид:

1

∂u

≈ A

σ′xz

n .

(11)

2

∂ z

В рассматриваемом приближении малых углов наклона

свободной

поверхности для компоненты σ′xz

имеет место

приближенное равенство:

σ′xz ≈ρ g (hs

− z)

∂hs

.

(12)

∂ x

Окончательно закон Глена (11) с учетом выражения (12) приводит к дифференциальному уравнению относительно горизонтальной компоненты скорости течения льда:

1		∂u		= A(ρ g)n (hs − z)n		∂hs		n .
2		∂ z				∂ x

Учитывая, что скорость возрастает от основания к поверхности и направлена противоположно градиенту уровня свободной

поверхности hs (x) , получим уравнение:
	∂u		∂hs			n−1	∂hs	.
		= −2 A(ρ g)n (hs − z)n							(13)
	∂ z		∂ x
							∂ x

Интегрирование уравнения (13) с учетом проскальзывания в базисном слое дает:

u(x,ξ) = ub − 2	A(ρ g)n		∂hs		n−1	∂hs		H n+1	(1 −ξ n+1 )	(14)
			∂ x			∂ x		n +1

где ξ = hsH− z .

Из выражения (14) непосредственно следует, что течение льда в рассматриваемом приближении определяется углом наклона свободной поверхности и не зависит от течения льда в соседних с точкой x областях. Это обстоятельство дает возможность обобщить

14

полученный результат на трехмерный случай, полагая, что горизонтальная составляющая скорости течения льда определяется

градиентом уровня свободной поверхности hs (x, y) :
ur(x, y,ξ) =−	2		r	r	n−1		(1−ξ n+1 ).
			A(ρ g)n hs	hs		H n+1		(15)
	n +1

§ 3. Уравнение поверхности ледникового покрова

Основываясь на результатах предыдущего параграфа, в приближении тонкого слоя задача определения изменений формы поверхности ледникового покрова со временем заключается в решении уравнений баланса массы (8) и переноса тепла (9).

Вектор q в уравнении баланса массы (8) для горизонтальной составляющей скорости течения льда (15) имеет вид:

r

2

n

r

r

n−1

n+2

q

=−

A(ρ g)

hs

hs

H

.

(16)

n + 2

Подстановка этого выражения в уравнение баланса массы (8) приводит к уравнению:

∂h

s

∂

2 A

(ρ g)

n

r

n−1

(hs − hb )

n

+

2

∂h

= a +

hs

s

+

∂t

∂ x n + 2

∂ x

(17)

∂

2 A

(ρ g)

n

r

n−1

(hs − hb )

n

+

2

∂h

s

hs

.

∂ y n + 2

∂ y

Далее, будем рассматривать ледниковый покров с постоянной температурой льда, т.е. коэффициент текучести льда A является постоянной величиной. Введем масштабы измерения координат L0 (линейные размеры основания), времени T0 и

толщины покрова Z0 . Тогда, в результате обезразмеривания

уравнения (17) получим уравнение поверхности ледникового покрова в виде:

∂ s

∂

r

n−1

(s −b)

n+2

∂s

=1

+

s

+

∂t

∂ x

∂ x

∂			r		n−1	(s −b)	n+2	∂s
			s							(18)
∂ y								∂ y

15

при условии, что масштабы измерения координат, времени и толщины покрова связаны между собою соотношениями:

2A(ρ g)n Z

a (n + 2)L

1

2n+2

n+1

Z

2(n+1)

0

0

= a , или

Z

0

=

0

; T

=

. (19)

n+1

n

(n + 2)L0

2 A(ρ g)

0

a

Таким образом, в приближении тонкого слоя задача определения прогнозов эволюции ледникового покрова сводится к решению уравнения эллиптического типа в следующей математической постановке:

∂ s

∂

∂ s

∂

∂ s

r

n−1

(s − b)

n+2

=1 +

+

k =

s

,

k

k

,

∂t

∂ x

∂ x

∂ y

∂ y

(20)

x, y Ω, t > 0;

s

= b(x, y);

t=0

s

= b

.

Γ

Γ

В такой постановке дополнительно предполагается, что в течение рассматриваемого промежутка времени границы области залегания ледникового покрова остаются неизменными.

Порядок значения толщины льда в окрестности вершины определяется линейными размерами основания области залегания ледникового покрова согласно выражению (19). Масштаб измерения

времени T0 определяет порядок времени накопления ледниковой

массы, т.е. порядок времени, за которое решение задачи (20) выходит на стационарное решение.

§ 4. Плоская модель течения льда в ледниковом покрове

Если линейные размеры основания ледникового покрова в направлении оси y много больше линейных размеров в

направлении x , т.е. ∂∂sy << ∂∂xs , то течение льда можно считать

16

плоским (§ 2). В этом случае задача (20) сводится к задаче для одномерного уравнения поверхности. Постановка этой задачи для случая плоского горизонтального основания ледникового покрова имеет вид:

n−1

∂s

∂

∂s

∂s

n+2

=1

+

, k =

s

, 0

< x <1, t > 0;

∂t

k

∂ x

∂ x

∂ x

=

0;

(21)

s

t =

0

∂s

= 0;

s

= 0.

x=1

∂ x

x=0

4.1. Форма поверхности стационарного ледникового купола

Существует аналитическое стационарного уравнения поверхности:

d

d s

n−1

n+2

1 +

s

d s

= 0 , или

1 =

d x

d x

d x

решение одномерного

d			d s			n
						s	n+2	.
d x			d x

Интегрирование этого уравнения с учетом граничного условия

∂s

= 0 приводит к уравнению с разделяющимися переменными:

∂ x

x=0

n

d s

n+2

1

x = sn+2

d s

, или −

s

n

= x

n

.

d x

d x

Соответственно, с учетом второго граничного условия s x=1 = 0 получим

0	~	n+2	~	1	~	1	~
		n				n
− ∫ s			ds	=∫ x			dx .
s				x

Окончательно, аналитическое решение для стационарной формы поверхности ледникового покрова в рамках плоской модели течения льда имеет вид:

17

	n			n+1		n
						2(n+1)
sst =2	2(n+1)		− x	n			.	(22)
		1

4.2. Консервативная разностная схема для уравнения поверхности (плоская модель течения льда)

Запишем уравнение баланса массы в стационарном

ледниковом	покрове,		форма				поверхности которого				определяется
		d			d s
уравнением	1 =−						,	на	отрезке	с	границами,
				k	d x
		d x
расположенными в полуцелых узлах									i −1/ 2 , i +1/ 2		равномерного
разбиения отрезка [0,1] (рис. 4):

∆x = qi+1/ 2 − qi−1/ 2 ,

где qi±1/ 2 – безразмерные значения потоков льда в единицу времени на единицу длины в направлении y через боковые границы, расположенные в узлах i ±1/ 2 . Они определяются выражениями:

qi+1/ 2 ≈ −ki+1/ 2

si+1 − si

;

qi−1/ 2

≈ −ki−1/ 2

si − si−1

;

∆ x

∆ x

где ki+1/ 2 =

s

i+1

− s

i

n−1

s

i

+ s

i+1

n+2

≡ki .

(23)

∆ x

2

i-1

i-1/2

i

i+1/2

i+1

Рис. 4. Шаблон разностной схемы

Таким образом, консервативная разностная схема для одномерного стационарного уравнения поверхности имеет вид:

18

1

s

i+1

− s

i

s

i

− s

i−1

1

= −

ki

−ki−1

.

∆ x

∆ x

∆x

Соответственно, неявная консервативная разностная схема для одномерного нестационарного уравнения поверхности будет иметь вид:

s	m+1 − s	m		1		sm+1	−sm+1	−kim−1	sm+1	− sm+1
i	i		=1 +		kim	i+1	i		i	i−1	.
	∆τ					∆ x			∆ x
				∆ x

Вопрос о линеаризации разностной схемы решается аналогично случаю нелинейного уравнения теплопроводности – значения коэффициента k определяются по значениям s на предыдущем временном слое. Окончательно разностная схема для задачи (21) имеет вид:

m+1

1

m

m+1

1

m

m

1

si−1

−

ki−1

+ si

(ki−1

+ ki

)+

+

∆x2

2

∆x

∆τ

m+1

1

m

m

si

+ si+1

−

ki

=1 +

,

i = 2...N −1;

(24)

∆x

2

∆τ

sm+1

= sm+1

; sm+1 = 0;

1

2

N

s0 = 0, i =1...N.

i

Схема (24) имеет первый порядок точности по времени и координате, вследствие аппроксимации граничного условия в т. x = 0 с первым порядком точности.

Для того чтобы схема имела второй порядок точности по координате, в т. x = 0 необходимо использовать уравнение баланса массы, вводя в рассмотрение дополнительные узлы в области x < 0 ,

а также условие		четности	функции		s	относительно	плоскости
ледораздела	( x = 0 ). Т.е.,		если узел			i находится	на	линии
ледораздела,	то	имеют		место		следующие	условия:
si−1 = si+1; ki−1 = ki .		Используя		эти	условия в уравнении			(24),

получим уравнение баланса массы в узле i =1. Таким образом, разностная схема второго порядка точности имеет вид:

19

m+1

1

m

m+1

1

m

m

1

si−1

−

ki−1

+si

(ki−1

+ ki

)+

+

∆x

2

2

∆x

∆τ

1

s m

+ sim+1+1

−

kim

=1 +

i

,

i = 2...N −

1;

∆x2

∆τ

(25)

2

1

2

sm

sm+1

k m

+

+sm+1

−

k m

=1 +

1

; sm+1

= 0;

1

1

∆τ

2

∆x2

1

∆τ

N

∆x2

s0 = 0, i =1...N.

i

Далее представлена программа численного решения задачи (21) (разностной схемы (25)), реализованная с помощью математического пакета Maple.

В качестве входных данных заданы следующие значения (§ 1): a = 0.3 м/год ; ρ = 910 кг/м3 ; A =10−16 Па−n год−1 ; n = 3 ;

g = 9.8 м/c2 ; L0 =105 м .

Решение системы линейных алгебраических уравнений (25) с 3-диагональной матрицей осуществлено посредством встроенной процедуры решения СЛАУ из пакета Linear Algebra.

На графиках в программе последовательно представлены аналитическое решение (22), расположение ненулевых элементов матрицы системы, уровни поверхности ледникового покрова в различные моменты времени, изменение толщины ледникового покрова на линии ледораздела ( x = 0 ) со временем. Время накопления ледниковой массы (время выхода решения задачи (25) на стационарное решение (22)) для выбранных значений входных

данных составляет ≈ 6 103 лет – значение представлено в конце программы.

Устойчивость разностной схемы (25) исследовалась непосредственным сравнением решения задачи (25), которое выходит на стационарное решение при t ≥1.8 , с аналитическим решением (22) стационарного уравнения. В частности, установлено, что для коэффициента вида (23) разностная схема (25) является условно устойчивой.

Значения шагов по времени ∆τ , для которых проведены вычисления, представлены в табл.1. В таблице также приведены

20