Коновалов Учебно-методическое пособие по курсу 2007

>

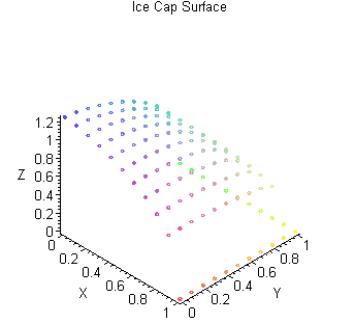
> L_P:=[seq(seq([L_x[i],L_y[j],S1[i,j]],j=1..No),i=1..No)]:

>

>

PLOT3D(POINTS(L_P),SYMBOL(CIRCLE),AXES(FRAME),TITL E("Ice Cap Surface"),AXESLABELS(X,Y,Z));

> #-------------------------------------------------------------

> Points:=[seq([seq(S1[i,j], j=1..No)],i=1..No)]:

>

plots[listcontplot](Points,contours=16,filled=true,linestyle=3,coloring =[blue,white],title="Ice Cap Surface");

51

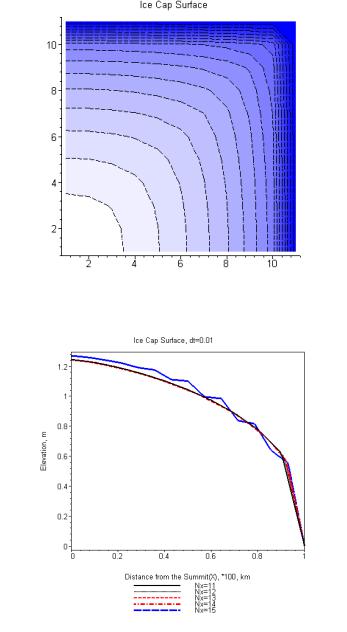
>Дополнение. Примеры неустойчивости схемы.

>#++++++++++++++++++++++++++++++++++++++++++++++++

>#++++++++ The examples of the model instability +++++++++++

>#++++++++++++++++++++++++++++++++++++++++++++++++

52

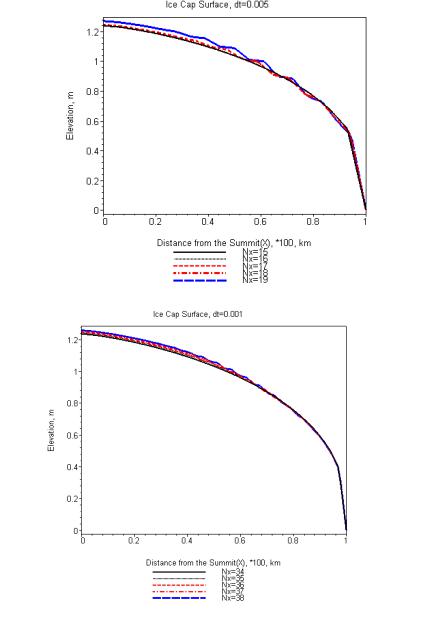
53

§ 7. Решение уравнения поверхности методом конечных элементов (методом Галеркина)

			Уравнение	поверхности задачи	(20) в области Ω
	эквивалентно уравнению:
		∂s	r
	∫∫		−1−div (k s) W dx dy =0		(38)
		∂t
	Ω

где W – произвольная непрерывная в области Ω функция, удовлетворяющая граничным условиям задачи (20): W Γ = 0 .

Учитывая это граничное условие и применяя теорему ГауссаОстроградского, уравнение (36) можно записать в виде:

	∂s		r r
				(39)
∫∫	∂t	−1 W dx dy +∫∫k W s dx dy = 0 .
Ω			Ω

Метод конечных элементов заключается в следующем. Узлы разбиения области Ω (в общем случае нерегулярной сетки) соединяются непересекающимися линиями. Таким образом, область Ω разбивается на элементарные непересекающиеся области (треугольники или четырехугольники) – конечные элементы. Эта процедура носит название триангуляции области ( Ω).

Рассмотрим произвольный p -й узел разбиения и конечные элементы, одной из вершин которых является данный узел.

Объединение этих элементов образует окрестность	p -го узла ωp .
Определим в ωp функцию g p , которая равна 1 в	p -м, является
заданным алгебраическим полиномом n -й степени	в каждом из

элементов окрестности ωp , обращается в 0 на границе ωp и равна тождественно 0 вне ωp . Например, в случае двумерной области Ω,

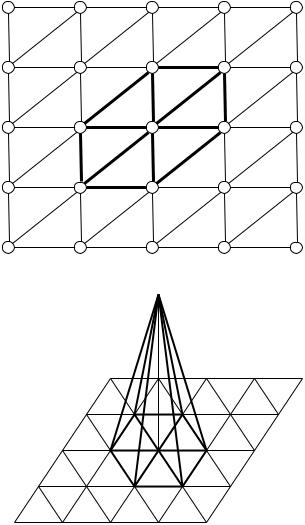
треугольных конечных элементов и полиномов 1-й степени геометрическим образом такой функции является пирамида (рис.6, рис.7). Построенные указанным способом в каждом узле разбиения

функции {g p }Np=1 образуют линейно независимую систему функций в пространстве C(Ω) – всех непрерывных в области Ω функций.

54

	i,j+1	i+1,j+1
i-1,j	i,j	i+1,j

i-1,j-1 i,j-1

Рис. 6. Схема узлов элементарной ячейки МКЭ

Рис. 7. Вид базисной функции МКЭ

Будем искать решение задачи (38) в подпространстве C(Ω), которое является линейной оболочкой L(g p ) – множества {g p }Np=1 .

55

Т.е. функции s ,W L(g p ) и, следовательно, могут быть

N

однозначно представлены в виде разложений s = ∑s p g p ,

p=1

N

W = ∑Wp g p . В этих разложениях s p и Wp – значения функций в

p=1

узлах разбиения.

Подставим указанные разложения в интеграл (39). Тогда, переходя к сумме интегралов по конечным элементам и вычисляя соответствующие интегралы (учитывая, что функции g p известны),

получим уравнение (разностную схему) относительно неизвестных значений s p (W – заданная функция).

Окончательно,	выбрав	в	качестве	W	N
линейнонезависимых в	L(g p )	функций,	получим	систему	N
линейных алгебраических уравнений относительно s p				(с отличным

от 0 определителем). В частности, в качестве таких функций могут быть взяты базисные функции g p .

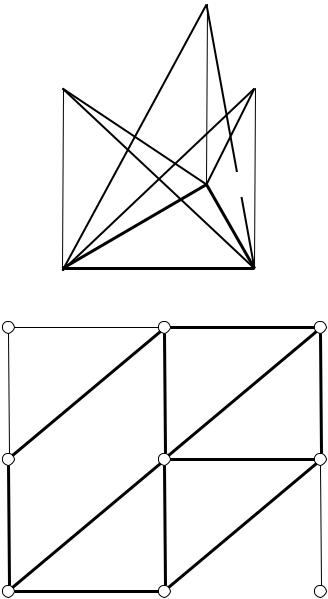
Далее, применим описанную выше процедуру к задачам (31) (или (36)), когда областью Ω является квадрат. Триангуляцию области осуществим для равномерной сетки, как показано на рис. 6. Будем рассматривать базисные функции g p , которые линейно

изменяются в каждом конечном элементе – это пирамиды, в основаниях которых лежат шестиугольники, образованные шестью конечными элементами (рис. 7). Тогда в любом конечном элементе (треугольнике):

	3	3	ϕEj (x, y);
s E (x, y,t)= ∑siE (t)ϕiE (x, y);		W E (x, y)= ∑wEj		(40)
	i=1	j=1
где	siE (t), wEj – значения функций в соответствующих узлах сетки,
ϕEj	– плоскости, образующие грани пирамид с вершинами в
соответствующих узлах (рис.8):
ϕEj	(x, y) = α Ej x + β jE y +γ Ej ,	j =1,2,3.

56

3

1		2
Рис. 8. Базисные функций в элементе
	i,j+1 (3)		i+1,j+1 (2)

											1
						2
															6		i+1,j (3)
	i-1,j (2)									i,j (1)
		3
											5
						4
i-1,j-1 (3)							i,j-1 (2)
				Рис. 9.								узлов
							Нумерация

57

Коэффициенты α Ej , β jE и γ Ej являются решениями СЛАУ:

x1Ex2E

x3E

где (xiE , yiE )

y	E			α	E				δ
					j
		1
1										1 j
y	E				E		=		δ		,
	2	1		β j						2 j
	E				E				δ
y3		1		γ j						3 j

– координаты вершин элемента (треугольника).

Представив интегралы в (39) в виде суммы интегралов по конечным элементам области Ω и подставляя в эти интегралы выражения (40), получим:

∂ s E

∫∫E

i

j

∂t

i

ϕ E ϕ E

dx dy +

∑wEj

∫∫k E (ϕiE,

x ϕ Ej, x +ϕiE,

= 0 ,

(41)

+ siE

y ϕEj, y )dx dy −

E

E

−

∫∫

ϕEj

dx dy

E

s

+ s

2

+ s

3

n+2

r

r

n−1

где

k E

=

1

(siE s Ej

( ϕiE , ϕEj

))2

, по

повторяющимся

3

индексам проводится суммирование.

Интегралы в выражении (41) соответственно равны:

∫∫ϕiE dx dy = a3E ;

E

	aE		, i =
∫∫ϕiEϕEj		6
	dx dy =
E	aE		, i ≠
		12

∫∫ϕiE, x ϕEj,x dx dy =αiE α Ej a E

j;

j.

E ;

58

∫∫ϕiE, y ϕEj, y dx dy =βiE β jE a E ; E

		1	1	1	1
где aE – площадь элемента:	aE =		xE	xE	xE	.
		2	1	2	3
			y E	y E	y E
			1	2	3

С учетом указанных выражений для интегралов и конечноразностной аппроксимации производной по времени уравнение (41) имеет вид:

1

,i

= j

∆

τ

(siE )m+1 6

+

1

, i ≠ j

12 ∆τ

∑∑wEj

a E +

(siE )m+1 (k E )m (αiEα Ej +βiE β jE )−

= 0 .

(42)

E i, j

1

,i = j

1

− (siE )m

6

∆τ

−

3

1

,i ≠ j

12 ∆τ

Чтобы получить систему уравнений относительно

N 2

неизвестных значений si, j

в узлах сетки, требуется

задать

N 2

линейно-независимых функций W и подставить соответствующие

значения

wj в

выражение

(42). Линейная

независимость

этих

функций обеспечивает отличие от нуля определителя матрицы СЛАУ, которая формируется согласно описанному в предыдущем параграфе алгоритму. Наиболее простой способ – взять в качестве таких функций базисные функции g p . Тогда, обозначив элементы с

общей вершиной в узле i, j и соответствующие вершины, как показано на рис. 9, получим следующую разностную схему:

59

m+1

1

6

E

6

E

E

E

2

E

2

si, j

∑a

+∑a

k

(α1

)

+ (β1

)

+

6∆τ

E=1

E=1

1

(a1

+ a2 )+ a1k1 (α31α11 + β31β11 )+ a2 k 2 (α32α12 + β32 β12 )

sim, j++11

+

12∆τ

1

(a2

+ a3 )+ a2 k 2 (α22α12 + β22 β12 )+ a3k 3 (α23α13 +

β23 β13 )

sim−1,+1j

+

12∆τ

1

m+1

3

4

3

3

3 3

3 3

4

4

4 4

4 4

si−1, j−1

(a

+ a

)+ a

k

(α

3

α1

+ β3 β1

)+ a

k

(α3 α1 + β3

β1

)

+

12∆τ

1

m+1

4

5

4

4

4 4

4 4

5

5

5 5

5 5

si, j−1

(a

+ a

)+ a

k

(α2

α1

+ β2

β1

)+ a

k

(α2α1

+

β2 β1 )

+

12∆τ

1

(a5

+ a6 )+ a5 k 5 (α35α15 + β35 β15 )+ a6 k 6 (α36α16 + β36 β16 )

sim+1,+1j

+

12∆τ

1

(a6 + a1 )+ a6 k 6 (α26α16 + β26 β16 )+ a1k1 (α21α11 + β21β11 )

sim+1,+1j+1

=

12∆τ

1

6

sim, j

6

sim, j+1

(a

)+

sim−1, j

(a

)+

E

E

1

2

2

3

=

∑a

+

∑a

+

+ a

+ a

3

6

∆τ

12 ∆τ

12 ∆τ

E=1

E=1

sm

(a

3

4

)+

s m

(a

4

5

)+

s m

(a

5

6

)+

sm

(a

6

1

);

i−1, j−1

+ a

i, j−1

+ a

i+1, j

+ a

i+1, j+1

+ a

12 ∆τ

12 ∆τ

12 ∆τ

12 ∆τ

1 < i

< N, 1 < j < N;

(43)

sm+1

= sm+1

= 0; 1 ≤ j ≤ N;

1, j

N , j

m+1

m+1

= 0; 1 < i < N;

si,1

= si,N

n+2

n−1

s

+ s

2

+ s

3

3

2

где k E =

1

∑si s j

(αiα j + βi β j

)

.

3

i, j=1

Соответственно, ненулевые элементы матрицы СЛАУ после преобразования двумерного массива неизвестных sim, j+1 в одномерный (см. § 6) равны:

60