Коновалов Учебно-методическое пособие по курсу 2007

>

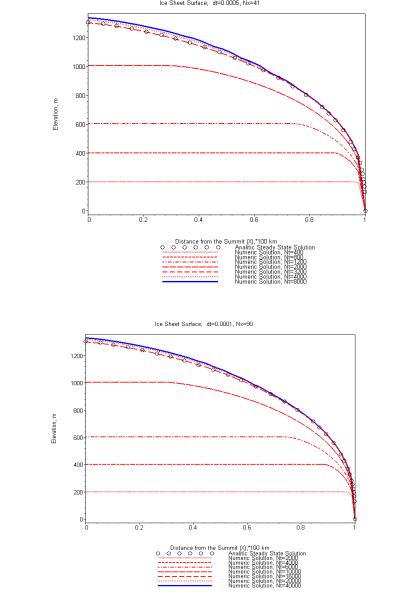
> #--- dt:=0.0005: Nx:=41: ---

> #--- dt:=0.0001: Nx:=90: ---

31

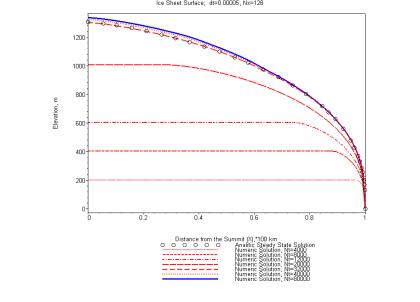
> #--- dt:=0.00005: Nx:=128: ---

§5. Аксиально-симметричый ледниковый купол

Вслучае, когда областью залегания ледникового покрова является круг, задача (20) обладает аксиальной симметрией. Соответственно, математическая постановка задачи для уравнения поверхности в случае аксиальной симметрии имеет вид:

n−1

∂s

1

∂

∂s

∂s

n+2

=1+

, k =

s

, 0

< r <1, t > 0;

∂t

r

rk

∂r

∂r

∂r

= 0;

(26)

s

t =0

∂s

= 0;

s

= 0.

∂r

r =1

r =0

32

5.1. Стационарная форма поверхности ледникового купола. Аналитическое решение

Алогично рассмотренному в предыдущем параграфе случаю плоского течения льда интегрирование уравнения поверхности стационарного аксиально-симметричного ледникового купола дает выражение, которое определяет форму поверхности:

	n−1			n+1		n
						2 (n+1)
sst = 2	2(n+1)		− r	n			.	(27)
		1

5.2. Консервативная разностная схема для уравнения поверхности в случае аксиальной симметрии

Консервативная разностная схема в случае стационарного,

	аксиально-симметричного ледникового			купола,				поверхность
			1	d		d s
	которого определяется уравнением 1	=−						, следует из
					rk	d r
			r d r

уравнения баланса массы льда в цилиндрическом слое между двумя

коаксиальными

цилиндрами,

проходящими через узлы i −1/ 2 ,

i +1/ 2 равномерного разбиения отрезка [0,1]:

2π ri ∆r = 2π ri+1/ 2 qi+1/ 2 −2π ri−1/ 2 qi−1/ 2 ;

где qi+1/ 2

≈ −ki+1/ 2

si+1

− si

;

qi−1/ 2 ≈ −ki−1/ 2

si − si−1

;

∆r

∆r

s

i+1

− s

i

n−1 s

i

+ s

i+1

n+2

ki+1/ 2 =

≡ ki .

∆r

2

Консервативная разностная схема в стационарном, аксиально-симметричном случае имеет вид:

33

1

r

+ r

s

i+1

− s

i

r

+ r

s

i

− s

i−1

1 = −

i

i+1

ki

−

i−1

i

ki−1

.

(28)

2

∆r

2

∆r

ri ∆r

Неявная консервативная разностная схема для нестационарного уравнения поверхности в аксиально-симметричном случае, соответственно, имеет вид:

sm+1			− sm
i				i			=1	+
		∆τ
		1					+ r
				r
+						i		i+1
	r						2
		∆r
	i

s

m+1

− s

m+1

r

+ r

s

m+1

− s

m+1 (29)

i+1

i

i

i−1

kim

−

i−1

i

kim−1

∆r

2

∆r

Консервативная разностная схема в узле i =1 ( r = 0 ) следует из уравнения баланса массы в цилиндре радиуса r3 / 2 = ∆r / 2 , которое в стационарном случае имеет вид:

π ∆r 2 / 4 = π ∆r q3/ 2 ; где q3 / 2 = −k1 s2∆−rs1 .

Соответственно, разностная схема в узле i =1 выглядит следующим образом:

	s2m+1 − s1m+1	=1 +	4	k1m (s2m+1 − s1m+1 ).
	∆τ		∆r 2

Окончательно, для задачи (26) получим следующую разностную схему второго порядка точности по координате:

34

r

+r

sim−1+1

−1

kim−1

+ sim+1

−

i

i

2r ∆r 2

i

r

+ r

+1

+ sim+1+1 −

i

i

kim

=1 +

2r ∆r 2

i

i = 2...N −1;

4

1

sm+1

k m +

+ sm+1

1

1

∆τ

2

∆r 2

si0 = 0, i =1...N.

+ r

r

+ r

1

r

−1

kim−1 +

kim +

i

i

i

i+1

+

2r ∆r 2

2r ∆r 2

∆τ

i

i

s m

i

,

∆τ

(30)

4

sm

−

k1m

=1

+

1

; sNm+1

= 0;

∆r 2

∆τ

Программа и результаты вычислений с помощью схемы (30) аналогичны результатам для одномерной задачи (21), рассмотренной в предыдущем параграфе. Отношение высот аксиальносимметричного ледникового купола и ледникового покрова (задача (21)) определятся решениями стационарных задач (27), (22) и для вершины составляет ≈ 0.92 (для n = 3 ). Соответственно, время накопления ледниковой массы (время выхода решения задачи (26) на стационарное) для аксиально-симметричного ледникового купола меньше, чем для ледникового покрова. Отношение времен составляет величину ≈ 0.85 .

Разностная схема (30), как и схема (25), устойчива при условии γ = ∆τ / ∆r 2 <α , где α ≈1.35 . Числа узлов разбиения по

координате, начиная с которых для заданного шага по времени проявляется нарушение сходимости численного решения, представлены в табл.2. Эти значения больше соответствующих

значений в табл.1 приблизительно в 1.3 ( 2 ) раза.

Таблица 2. Параметры шагов программы
∆τ	2 10−2	10−2	5 10−3	2 10−3	10−3	5 10−4
Nmax	10	13	18	27	38	54
∆τ / ∆r 2	1.62	1.44	1.44	1.35	1.37	1.4

35

Продолжение табл. 2.
∆τ	2 10−4	10−4	5 10−5
Nmax	85	120	170
∆τ / ∆r 2	1.41	1.42	1.43

Далее, рассмотрены методы численного решения задачи для двумерного уравнения поверхности ледникового покрова.

§ 6. Консервативная разностная схема для двумерного уравнения поверхности

Рассмотрим случай, когда областью залегания ледникового покрова является квадрат, и построим консервативную разностную для двумерного уравнения поверхности.

Математическая постановка задачи в этом случае имеет вид:

∂ s

∂

∂ s

∂

∂ s

=1

+

+

∂t

k

∂ y

k

, k

∂ x

∂ x

∂ y

0 < x <1, 0 < y <1, t > 0;

s

t=0

=

0;

s

= 0.

Γ

			2				2		n−1
	∂ s				∂ s				2
=				+
	∂ x				∂ y

s n+2 ,

(31)

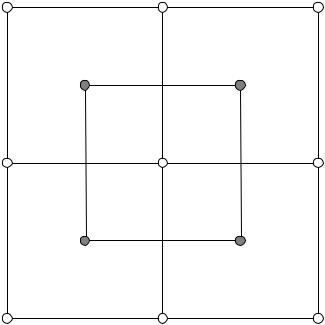
Аналогично рассмотренным в предыдущих параграфах пространственно-одномерным случаям, консервативная разностная схема для двумерного уравнения в стационарном случае может быть получена, исходя из баланса массы в прямоугольном параллелепипеде, основанием которого является квадрат с вершинами в полуцелых узлах (рис. 5):

36

i+1/ 2, j+1/ 2				i−1/ 2, j+1/ 2			i+1/ 2, j+1/ 2				i+1/ 2, j−1/ 2
∆2 −	∫qx dy +			∫qx dy −				∫qy dx +			∫qy dx =0 ; (32)
i+1/ 2, j−1/ 2				i−1/ 2, j−1/ 2			i−1/ 2, j+1/ 2				i−1/ 2, j−1/ 2
		∂ s			∂ s			r	n−1	sn+2	; ∆ – шаг координатной
где qx	= −k		; qy = −k			; k =		s
		∂ x			∂ y

сетки.

i-1, j+1

i, j+1

i+1, j+1

i-1/2, j+1/2		i+1/2, j+1/2

i-1, j	i, j		i+1, j

i-1/2, j-1/2		i+1/2, j-1/2

i-1, j-1

i, j-1

i+1, j-1

Рис. 5. Шаблон разностной схемы для двумерной задачи

37

Аппроксимация интегралов методом прямоугольников приводит к следующей разностной схеме:

si

+1, j − si, j

ki+1/ 2, j+1/ 2

+ ki+1/ 2, j−1/ 2

−

∆

2

si, j − si−1, j

ki−1/ 2, j+1/ 2 + ki−1/ 2, j−1/ 2

−

+

∆

2

=0 .

(33)

∆2 + ∆

+

si, j+1 − si, j

ki−1/ 2, j+1/ 2 + ki+1/ 2, j+1/ 2

−

∆

2

si, j − si, j−1

ki−1/ 2, j−1/ 2 +ki+1/ 2, j−1/ 2

−

∆

2

Выражение, аппроксимирующее коэффициент k

в полуцелом узле

i +1/ 2, j +1/ 2 со вторым порядком точности, имеет вид:

(si+1, j − si, j + si+1, j+1 − si, j

2

n−1

2

ki+1/ 2, j+1/ 2

1

+1 )

≈

+

(s

− s

+ s

− s

(34)

4 ∆2

i, j+1

i, j

i+1, j+1

i+1, j

)2

((si, j + si+1, j + si, j+1 + si+1, j+1 )/ 4)n+2 ≡ ki, j .

Соответственно, из схемы (33) с учетом (34) следует, что неявная консервативная схема для нестационарного уравнения поверхности в рассматриваемой задаче (31) имеет вид:

38

m+1

1

1

m

m

m

si, j

+

(ki, j + ki, j−1

+ki−1, j

2

∆τ

∆

−

1

(kim, j +kim, j−1 ) +

sim+1,+1j

2

2 ∆

1

m

m+1

m

si, j+1

−

(ki−1, j + ki, j )

+

2

2 ∆

m+1

1

m

m

si, j−1

−

(ki−1, j−1

+ ki, j−1 )

+

2

2 ∆

−

1

(kim−1, j + kim−1, j−1 ) =

sim−1+,1j

2 ∆2

sim, j

; 1 < i < N, 1 < j < N;

=1 +

∆τ

= sm+1

sm+1

= 0; 1 ≤ j ≤ N;

1, j

N , j

m+1

m+1

= 0; 1 < i < N.

si,1

= si,N

+ kim−1, j−1 )	+

(35)

Решение задачи (35) сводится к решению СЛАУ, которая образуется после перехода от двумерного массива значений si, j к

одномерному массиву посредством взаимнооднозначного соответствия между множеством узлов координатной сетки и

множеством натуральных чисел отрезка [1, N 2 ]:

(i, j)↔ (i −1)N + j .

Таким образом, столбец неизвестных значений СЛАУ состоит из N столбцов, и каждый i-й столбец содержит N элементов s(i−1)N + j , 1 ≤ j ≤ N .

Соответственно, разностной схеме (35) в узле i, j соответствует уравнение (строка матрицы Ap,q ) СЛАУ с номером

(i −1)N + j . Ненулевыми элементами этой строки (для внутреннего узла) будут следующие элементы:

39

A(i−1)N + j, (i−1)N + j =

1

+

1

(kim, j +kim, j

−1 + kim−1, j +kim−1, j−1 );

∆τ

2

∆

A(i−1)N + j,i N + j =−

1

(kim, j + kim, j−1 );

2

2∆

1

(kim−1, j + kim, j );

A(i−1)N + j, (i−1)N + j+1 = −

2

2 ∆

A(i−1)N + j, (i−1)N + j−1 = −

1

(kim−1, j−1 + kim, j−1 );

2

2 ∆

A(i−1)N + j, (i−2)N + j =−

1

(kim−1, j + kim−1, j−1 ).

2

2

∆

Учитывая симметрию ледникового купола относительно

плоскостей x =1/ 2 ,

y =1/ 2 ,

с целью уменьшения объема

вычислений задача для уравнения поверхности может быть рассмотрена в области, соответствующей 1/4 части ледникового купола. Т.е. задачу (31) можно рассматривать в следующей математической постановке:

∂ s

∂

∂ s

∂

∂ s

=1 +

+

∂t

k

∂ x

∂ y

k

, k

∂ x

∂ y

0 < x <1, 0 < y <1, t > 0;

s

t=0

= 0;

∂ s

= 0;

∂ s

= 0;

s

x=1 =

∂x

x=0;

∂ y

y=0;

0≤y<1

0≤x<1

			2				2		n−1
	∂ s				∂ s				2
=				+
	∂ x				∂ y

0; s y=1 = 0.

s n+2 ,

(36)

Аналогично одномерному случаю разностная схема для задачи (35) будет иметь второй порядок точности по координате, если на границах квадрата x = 0 , y = 0 использовать разностную схему для

уравнения поверхности во внутренних узлах, учитывая условия симметрии: si−1, j = si+1, j , ki−1, j = ki, j (на границе x = 0 ) и

40