Ломоносова Сборник задач по квантовой електродинамике 2010

Процессу (б) соответствует диаграмма рис. 11 б, согласно которой функция Грина процесса есть:

Dµν (x2 − x1) = − d4yd4xDµλ(x2 − y)[−ıe(γλ)ab]

Sbc(y − x)[−ıe(γσ )cd]Sda(x − y)Dσν (x − x1),

где индексами a, b, c, d отмечены матричные элементы соответствующих матриц. Выражение для функции Грина можно записать в виде:

Dµν (x2 − x1) = −(−ıe)2 d4xd4yDµλ(x2 − y)Dσν (x − x1)

Sp [γλS(y − x)γσ S(x − y)].

Напомним, что дополнительный знак минус в правых частях приведенных формул ставится по особому фейнмановскому правилу для электронной петли. Отметим, что последнее соотношение является поправкой к причинной функции Грина фотона за счет процесса поляризации вакуума – образования и поглощения пары «фермион-антифермион». Эта поправка второго порядка по константе электромагнитного взаимодействия e.

Процессу (в) отвечает диаграмма рис. 11 в. Она не соответствует никакому наблюдаемому физическому процессу. Это типичная флуктуация физического вакуума, в котором постоянно порождаются и уничтожаются фотоны и фермион-антифермион- ные (электронно-позитронные) пары. Эти флуктуации и образуют физический вакуум, который совсем не является пустым. Именно на фоне такого вакуума, заполненного всевозможными флуктуациями, осуществляются физические процессы взаимодействия частиц, которые взаимодействуют не только между собой, но и с флуктуациями вакуума. Сравнение теоретических предсказаний с экспериментальными данными свидетельствует о необходимости учитывать такие взаимодействия. Примером взаимодействия фермиона с флуктуацией типа рисунка в является процесс, изображенный на диаграмме рис. 11 г. В результате таких взаимодействий точная причинная функция Грина свободного физического

141

фермиона существенно отличается от функции Грина фермиона без учета взаимодействия с вакуумными флуктуациями собственного поля.

7.Электродинамические процессы

7.1.Электродинамические процессы в низшем порядке

теории возмущений

114. В наинизшем порядке теории возмущений процесс упругого eµ-рассеяния описывается одной диаграммой Фейнмана, изображенной на рис 12.

e	p1	p3	e
µ			µ
	p2	p4

Рис. 12

Инвариантная амплитуда T имеет вид:

e2

T = (p3 − p1)2 (¯u3γµu1)(¯u4γµu2),

где биспиноры u1,2, u¯3,4 описывают начальные и конечные состояния e и µ. Эрмитовски сопряженная амплитуда T † дается выражением:

T † =	e2
	(p3 − p1)2 (¯u1γν u3)(¯u2γν u4).

142

Предполагая, что начальные и конечные частицы, участвующие в процессе, не поляризованы, усредним квадрат модуля амплитуды |T |2 = T †T по поляризационным состояниям начальных частиц и просуммируем по поляризационным состояниям конечных частиц:

e4

λ1λ2 3

4

|T |2 = 4(p3

−

p1)4

(¯u1λ1 γν u3λ3 )(¯u2λ2 γν u4λ4 )(¯u3λ3 γµu1λ1 )(¯u4λ4 γµu2λ2 )=

λ λ

=

e4

λ1λ3 u¯1λ1

γν u3λ3 u¯3λ3 γµu1λ1

λ2,λ4 u¯2λ2

γν u4λ4 u¯4λ4 γµu2λ2

=

4(p3

−

p1)4

e4

= 4(p3 − p1)4 [Sp (pˆ1 + m)γν (pˆ3 + m)γµ][Sp (pˆ2 + µ)γν (pˆ4 + µ)γµ] =

4e4

= (p3 − p1)4 [p3µp1ν + p3ν p1µ + (m2 − (p1p3))gµν ]× ×[p2ν p4µ + p2µp4ν + (µ2 − (p2p4))gµν ] =

8e4

= (p3 − p1)4 [(p2p3)(p1p4) + (p3p4)(p1p2) + (m2 −(p1p3))(p2p4)+ +(µ2 − (p2p4))(p1 p3) + 2(m2 − (p1p3))(µ2 − (p2p4))].

Здесь m и µ – массы электрона и мюона. Выразим скалярные произведения 4-импульсов, входящих в полученную выше формулу, через инвариантные переменные s, t и u (см. задачу 22):

(p1p2) = (p3p4) = s−µ2−m2

;

(p1p3) = 2m2 −t ;

(p2p4) = 2µ2−t ;

2

2

2

(p1p4) = (p2p3) =

m2

+µ2−u

2

2

. Тогда величину |T | можно записать в

виде:

2e4

m2

+ µ2

|T |2 =

[s2 + u2 + 4(m2 + µ2)(t −

)].

t2

2

Переменные s, t и u связаны с полной начальной энергией

E сталкивающихся частиц, углом рассеяния θ0

и импульсом p0

каждой из них в ц-системе следующим образом (см. задачу 22): s = E2; t = −4p20sin2 θ20 ; u = 2m2 + 2µ2 − E2 + 4p20sin2 θ20 .

143

Для |T |2 получим в ц-системе выражение:
						e4
	|T |2 =						[E4 + (m2 + µ2)2 − 2(m2 + µ2)E2+
					4p4sin4 θ0
				0		2
							+ 8p04sin4	θ0	− 4E2 p02sin2	θ0	].
								2		2

Подставим это выражение в формулу для дифференциального сечения и, проведя интегрирование по фазовому объему (см. задачу 33), окончательно получим:

dσ	=	α2		[E4 − 2E2(m2 + µ2) + (m2 + µ2)2−
dΩ		16E2 p4 sin4 θ0
		0	2
				− 4E2p02 sin2	θ0	+ 8p04 sin4	θ0	],
					2		2

где p20 = [E2 − (µ + m)2][E2 − (µ − m)2]/4E2 , dΩ = d(cos θ0)dφ0, e2 = 4πα, α = 1/137, так как заряд здесь измеряется в хевисайдов-

ской системе единиц. В нерелятивистском по мюону приближении (p0 µ) выражение для дифференциального сечения превращается в формулу для рассеяния электрона на тяжелой заряженной частице:

dσ	=	α2(1 − v2 sin2 θ20 ) .
dΩ		4v	p0 sin		2
		2	2	4	θ0

где v = p0/ε – скорость электрона, ε – его энергия. Здесь учтено, что при p0 µ энергия электрона ε µ. Отметим, что для нерелятивистского электрона (v 1) полученное соотношение переходит в формулу Резерфорда. В ультрарелятивистском пределе (p0 µ) из точной формулы для дифференциального сечения следует приближенное выражение:

dσ	=	α2(1 + cos4 θ20 ) .
dΩ		8p0 sin		2
		2	4	θ0

144

115. Если электрон в конечном состоянии поляризован, то суммирование по его поляризациям отсутствует (сравните с задачей 114). Тогда в терминах предудущей задачи в соотношении для суммирования по поляризациям будет сохраняться множитель uλ3 (p3)¯uλ3 (p3), который на основании результата задачи 86

равен матричному оператору (матрице плотности) Λ+ = 12 (pˆ3 +m)(1−γ5sˆ3), где 4-вектор спина частицы sµ определен

в задаче 75. После суммирования и усреднения по поляризациям

остальных частиц квадрат инвариантной амплитуды |T |2 примет вид (сравните с аналогичной формулой предыдущей задачи):

		e4		1		(pˆ3 + m)(1 − γ5sˆ3)γµ]×
|T |2 =			[Sp (pˆ1 + m)γν
		(p3 − p1)4			2
						2e4
× [Sp (pˆ2 + µ)γν (pˆ4 + µ)γµ] =							[p3µp1ν + p3ν p1µ+
				(p3 − p1)4

+(m2 − (p1p3))gµν − ım αβµν p3αs3β + ım αµβν s3αp1β ]×

×[p2ν p4µ + p4ν p2µ + (µ2 − (p2p4))gµν ].

Поскольку слагаемые, содержащие 4-вектор спина вторичного электрона s3α, являются антисимметричными по индексам µ и ν (тензор µναβ антисимметричен при перестановке индексов) и умножаются на симметричный тензор по индексам µ, ν, полученный от вычисления следа для мюонов, то спиновые характеристики вторичного электрона вклада в процесс не дают, то есть конечный электрон рождается неполяризованным. Дифференциальное сечение совпадает с ответом предыдущей задачи. Полученный результат согласуется с сохранением проекций спина на любую ось квантования.

116. Рассмотрим 4-вектор поляризации частицы sµ (см. задачу 75) в ультрарелятивистском приближении E m, |p| m,

	(ξp)		(ξp)p	E	E
|p| ≈ E. sµ = (		, ξ+		) ≈ ( m	(ξn), m	(ξn)n), где ξ – единич-
	m		m(E+m)

ный вектор, совпадающий с удвоенным значением вектора спина s частицы в системе, где она покоится; n – единичный вектор вдоль направления импульса частицы. Выберем направление оси z вдоль импульса частицы, тогда pµ (E, 0, 0, E). Матричный

145

оператор Λ+

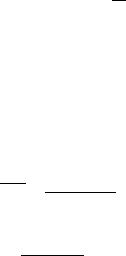
в ультрарелятивистском приближении упрощается:

Λ+ =					1	(pˆ+m)(1−γ5sˆ)	≈	1		(E(γ0 −γ3)+m)(1−γ5(s0γ0 −sγ)) =
					2			2
=	1								E					1
			[E(γ0 − γ3) + m][1				−				(ξn)γ5(γ0 − γ3)] =				[E(γ0 − γ3)−
		2							m					2
	E2
−				(ξn)(γ0 − γ3)γ5(γ0 − γ3) + m − E(ξn)γ5(γ0 − γ3)] =
	m
								1						1
									=				pˆ(1 + (ξn)γ5) =		pˆ(1 + λγ5).
												2		2

Величина λ = ξn – спиральность частицы (удвоенная проекция ее спина на направление импульса). Наиболее сильно растущее с энергией слагаемое Em2 исчезает в силу свойств γ-матриц:

(γ0 − γ3)γ5(γ0 − γ3) = γ5(−γ0 + γ3)(γ0 − γ3) =

= γ5(−γ02 − γ32 + γ0γ3 + γ3γ0) = 0.

Теперь упростим квадрат инвариантной амплитуды в ультрарелятивистском приближении по электрону E1, E3 m, а также будем считать начальный и конечный электроны поляризованными. Тогда для суммирования по поляризациям всех участвующих в процессе частиц получим выражение (сравните с задачей 114):

e4

|T |2 = 8(p3 − p1)4 Sp [pˆ3(1 + λ3γ5)γν pˆ1(1 + λ1γ5)γµ]× × Sp [(pˆ4 + µ)γν (pˆ2 + µ)γµ] =

2e4

= (p3 − p1)4 (1 + λ1λ2)(p1µp3ν + p1ν p3µ − (p1p3)gµν )×

× (p4µp2ν + p4ν p2µ + (µ2 − (p2p4)))gµν .

Множитель в первой скобке полученного выражения отличен от нуля, только когда спиральности начального и вторичного электронов совпадают.

117. В низшем порядке теории возмущений процесс описывается единственной фейнмановской диаграммой, изображенной на рис. 13.

146

e+ −p2

p1

e−

p3 µ−

−p4 µ+

Рис. 13

Инвариантная амплитуда T определяется выражением:

e2

T = (p1 + p2)2 [¯v(p2)γµu(p1)][¯u(p3)γµv(p4)].

Стандартные вычисления, которые мы опускаем, приводят к следующему результату для углового распределения мюонов в ц- системе:

dΩ

= 64| π|2

s

s

−4m2

= 16π2s3

s −

4m2

×

dσ

T 2

s

4µ2

e4

s

4µ2

−

−

1

×[(m2 + µ2)(s + m2 + µ2 − t − u) +

(t2 + u2)],

2

где s = (p1 + p2)2 = (p3 + p4)2 = 4E2

(E0 – энергия каждой из ча-

стиц

пары

e+e−

0

µ+µ−

в

ц-системе),

или

t = (p1−p3)2 = (p2−p4)2 = m2+µ2−2E02 +2

E02 − m2

E02 −µ2

cos θ0,

u = (p1 −p4)2 = (p2 −p3)2 = m2+µ2 −2E02 −2

E02 − m2

cos θ0

E02 −µ2

θ

относительно направле-

( 0 – угол вылета отрицательного мюона

ния движения электрона в ц-системе). В ц-системе реакции угловое распределение принимает вид:

dΩ	= 16E06
				E2	−m2 [E0 (m +µ +E0 )+(E0 −m )(E0 −µ )cos θ0].
dσ		α2		E2	µ2		2	2	2	2	2	2	2	2
			0		2

0 −

Здесь dΩ = d(cos θ0)dφ0.

147

Отметим, что угловое распределение вторичных мюонов симметрично относительно угла θ0 = π2 (содержит слагаемые четных степеней по cos θ0). Минимум распределения отвечает углу θ0 = π2 . Наиболее простой вид угловое распределение прнимает в ультрарелятивистском случае при высоких энергиях e+e−-пары

(E0 µ):
	dσ	=	α2	(1 + cos2	θ0),
	dΩ		4s

Интегрируя выражение для точного углового распределения по телесному углу dΩ, получим полное сечение процесса:

σ = 3E2						2E2	+ 4E4
			E2	−m2 1 +
	πα2		E2	µ2		m2 + µ2		m2	µ2	!
0			0 −			0			0
			0
или при высоких энергиях e+e−-пучка (E0										µ): σ = πα22 .
										3E0	а для
118. Амплитуда, соответствующая диаграмме рис. 14

электрона или рис. 14 б для позитрона, представляется выражением:

		ˆ		ˆ	− p1)v(p2),
Te− = −eu¯(p2)A(p2			− p1)u(p1), Te+ = ev¯(p1)A(p2
ˆ	Ze	γ0, q = p2		− p1, e < 0.
где A(q) = −q2

e−		e−	e+	e+
p1	p2		−p1	−p2
	а			б
			Рис. 14

148

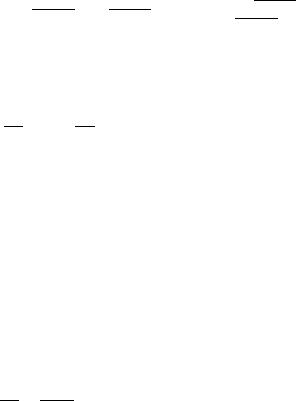
Покажем, что в низшем порядке теории возмущений неполяризованный электрон (или позитрон) при кулоновском взаимодействии после столкновения не приобретает поляризации. Причину отсутствия эффекта поляризации легко понять, исходя из структуры матричного элемента. Рассмотрим выражение u¯2γ0u1 и представим его в двухкомпонентной форме:

u¯(p2)γ0u(p1) = u†(p2)u(p1) =

√

= &√E + mw†, √E − mw†(σn2)' √ E +(mw ) = E − m σn1 w

=(E + m)w†w + (E −m)w†ıσ[n2 ×n1]w + (E −m)(n1n2)w†w =

=(E + m)w†w + (E − m) cos θ w†w + (E − m)w†ı(σn) sin θ w.

Здесь E = E1 = E2, θ – угол рассеяния (угол между p1 и p2),

n1 = p1 , n2 = p2 – единичные векторы, направленные вдоль

|p1| |p2|

импульсов начальной и конечной частицы; n = [n1 ×n2] – единичный вектор, нормальный к плоскости рассеяния.

Таким образом, зависящая и не зависящая от спина части амплитуды рассеяния имеют разность фаз, равную π2 . Поэтому они не могут интерферировать в квадрате модуля матричного элемента (см. также задачи 115, 116). Поляризация же является результатом такой интерференции, которая должна быть пропорциональна (σn). Аналогичное доказательство справедливо и для случая рассеяния позитронов кулоновским полем.

119. Возведя в квадрат амплитуду Te+ , записанную в предыдущей задаче, усреднив по начальным поляризационным состояниям и просуммировав по конечным поляризационным состояниям, получим выражение:

dσ α2Z2

dΩ = 2q4 Sp (pˆ1 − m)γ0(pˆ2 − m)γ0,

где q2 = (p1 − p2)2 = 4p2 sin2 (θ/2) (θ – угол рассеяния); |p1| = |p2| = p; E1 = E2 = E. После вычисления следа окон-

149

чательно получим:
	dσ	=	Z2α2		1 − v2 sin2	θ	,
	dΩ		4p2v2 sin4	2θ		2

где v = Ep – скорость рассеиваемых позитронов. Точно такой же ответ получается и для рассеяния электронов в кулоновском поле ядра с зарядом (−Ze).

Полученное выражение отличается от классической формулы Резерфорда множителем (1 − v2 sin2 (θ/2)), который при низких энергиях стремится к 1 и возникает за счет взаимодействия заряда ядра с электрическим полем, создаваемым спиновым магнитным моментом движущегося электрона.

120. В низшем порядке теории возмущений процесс упругого рассеяния электрона на электроне описывается двумя диаграммами Фейнмана (рис. 15 а, б ).

p1

p3

p1

p4

p2	p4	p2	p3
	а		б

Рис. 15

Первая из диаграмм а аналогична диаграмме рассеяния электрона на мюоне; вторая диаграмма б возникает вследствие тождественности электронов. Соответствующая им амплитуда имеет следующий вид:

(¯u(p

3

)γ u(p

))(¯u(p

)γ (p

2

))

(¯u(p

4

)γ u(p1))(¯u(p3)γµu(p2))

!.

T = e2

µ

1

4

µ

−

µ

(p1

p3)2

(p1

−

p4)2

−

150